式による説明（３）　知らないと解けない難問２題

「式による説明」、ほとんどの問題は「（１）数の表し方」を覚えて、「（２）答えの書き方」が頭に入っていたら楽に解けます。

しかし、それだけでは解けない問題が２つ、あります。

一つは、「各位の数をたしたら３（または９）でわれる数は、３（または９）の倍数である」ことを説明する問題、もう一つは、「図形の問題で、同じものを２つの式で表す」問題です。

この２つは、それぞれの書き方を知っていないと正しい答えを書けません。

例題１：３けたの整数９８１の各位の数の和９＋８＋１＝１８は、９の倍数である。このとき、９８１は９の倍数になっている。このように、各位の数の和が９の倍数になる３けたの整数は９の倍数である。このことを説明せよ。

（答え）

・１００の位の数がａ、１０の位の数がｂ、１の位の数がｃである３けたの数を１００ａ＋１０ｂ＋ｃとする。

・１００ａ＋１０ｂ＋ｃ
＝９９ａ＋ａ＋９ｂ＋ｂ＋ｃ
＝９９ａ＋９ｂ＋ａ＋ｂ＋ｃ

各位の数の和が９の倍数なので、ｎを整数とするとａ＋ｂ＋ｃ＝９ｎと表せる。

９９ａ＋９ｂ＋ａ＋ｂ＋ｃ
＝９９ａ＋９ｂ＋９ｎ
＝９（１１ａ＋ｂ＋ｎ）

・１１ａ＋ｂ＋ｎが整数なので、９（１１ａ＋ｂ＋ｎ）は９の倍数である。
以上より、各位の数の和が９の倍数になる３けたの整数は９の倍数である。

（知っておかないといけないこと）

赤字で示した、９の倍数になるように（９でくくれるように）、１００ａ＝９９ａ＋ａ、１０ｂ＝９ｂ＋ｂに変形すること、ａ＋ｂ＋ｃが９の倍数なので９ｎと置き換えること、この２つの部分は、そうなることを理解したうえで、暗記、覚えておかないと、思いつくことなど不可能だと思います。

同じ種類の問題で、３の倍数であることを説明する問題があります。
このときは、１００ａ＋１０ｂ＋ｃ＝９９ａ＋９ｂ＋ａ＋ｂ＋ｃとするところは同じで、ａ＋ｂ＋ｃ＝９ｎを、ａ＋ｂ＋ｃ＝３ｎに変えるだけです。

例題２：おうぎ形で、半径をｒ、弧の長さをＬ、中心角をａ度、面積をＳとすると、Ｓ＝１／２Ｌｒが成り立つことを説明せよ。

（答え）

おうぎ形おうぎ形の面積＝円の面積×（中心角／３６０）だから、
面積Ｓ＝ｒ×ｒ×π×（ａ／３６０）・・・（１）

弧の長さ＝円周×（中心角／３６０）より、
弧Ｌ＝ｒ×２×π×（ａ／３６０）・・・（２）

（ここで、Ｓ＝１／２Ｌｒをつくるために、ＬをＳの式にはめ込むにはどうしたらよいかを考えます。（１）の式と（２）の式を眺めると、赤字の部分ｒ×π×（ａ／３６０）が同じことに気づきます。）

（１）より、ｒ×π×（ａ／３６０）＝Ｓ／ｒ
（２）より、ｒ×π×（ａ／３６０）＝Ｌ／２

よって、Ｓ／ｒ＝Ｌ／２

両辺にｒをかけて、
Ｓ＝ｒ×Ｌ／２
＝１／２Ｌｒ

だから、Ｓ＝１／２Ｌｒが成り立つ。

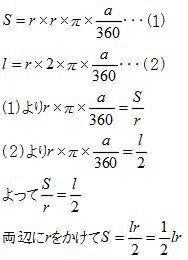
（知っておかないといけないこと）

まず、面積を式で表す。次に弧の長さを式で表す。
別々に２つの式を作った後、２つの式からできる等式を「むりやり」つくってしまうのがこつです。

中３の『式による説明』では、このタイプの問題がよく出ます。

この種類の問題も、練習して、書き方を知っておかないと、おそらく初見では解けません。