定滑車・動滑車・組み合せ滑車

滑車のすべての問題は、２つの原理さえ理解できれば簡単に解けるようになります。

原理１：１本の糸にはたらく力の大きさはすべて等しい。
図で、左に引く力が１なら、右に引く力も１です。

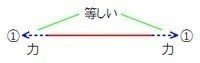
糸を滑車にかけても、この原理は変わりません。

図で、左下に引く力が１なら、右下に引く力も１です。

原理２：上に引っ張る力の和と下に引っ張る力の和はつねに等しい。

例えば、滑車を上に２つの力で引くとき、１つの力を１とすると、上に引く力は２つの力を合わせて１＋１＝２となります。
その力とつりあう、下に引く力は２です。

滑車を上に３つの力で引くとき、上に引く力の和は１＋１＋１＝３となり、下に引く力は３の大きさになります。

定滑車と動滑車

定滑車・・・固定されて動かない滑車が定滑車です。
糸を下に引くと、おもりは上に上がります。
「１本の糸にはたらく力は等しい」より、糸を引く力は、おもりの重さ（おもりにはたらく重力）と同じ大きさの力です。

糸を引く力＝おもりの重さ

糸を下に引いた長さと同じ長さだけ、おもりは上に上がります。

糸を引く長さ＝おもりがあがる長さ

動滑車・・・おもりが滑車にぶらさがっていて、おもりと一緒に滑車も動くのが動滑車です。
糸を上に引くと、おもりも動滑車も上に上がります。

「上に引っ張る力と下に引っ張る力は等しい」より、図で、動滑車にかかった糸の左の部分と右の部分の滑車を上に引く力の和（合計）が、おもりが滑車を下に引く力（おもりの重さ）と等しくなります。

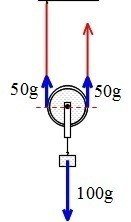
また、「１本の糸にはたらく力は等しい」より、糸の左の部分と右の部分とは同じ大きさの力です。

だから、糸が滑車を上に引く２つの力は等しく、ともにおもりの重さの半分（1/2）だということになります。

糸を引く力＝おもりの重さの半分（1/2）

また、下の図を見たらわかるように、糸を上に引く長さは、おもりが上に上がる長さの２倍になります。

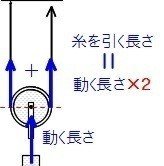
動滑車の２糸を引く長さ＝おもりが上にあがる長さの２倍

（糸を引く長さが2倍になることを、さらに詳しく説明すると・・・）

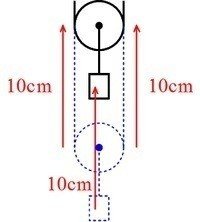
一つの例として、おもりを10cm上に引き上げるときを考えてみましょう。

図で、おもりが上に10cm上がるとき、おもりをつりさげている滑車も、10cm上に上がります。

このとき、滑車が10cm上に上がると、糸は、糸の青の点線の部分である、10cm+10cm=20cm引き上げられていることが、図よりわかります。

では、ここまで学んだことを使って、まず基本的な問題を解いてみましょう。

例題１：図１、図２のように、滑車を使って100gのおもりを持ち上げました。滑車の重さを考えないものとして、次の問いに答えなさい。

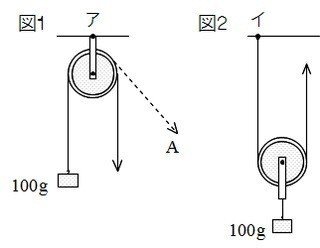
（１）図１、図２でおもりを持ち上げるとき、ひもを引く力はそれぞれ何gですか。

（２）図１、図２でおもりを10cm持ち上げるとき、ひもをそれぞれ何cm引けばよいですか。

（３）図１のア点、図２のイ点には、それぞれ何gの力が力がはたらいていますか。

（４）図１で、ひもを引く方向をAの向きにかえておもりを持ち上げるとき、ひもを引く力は何gになりますか。

（考え方と解答）

（１）図１、図２でおもりを持ち上げるとき、ひもを引く力はそれぞれ何gですか。

図１は定滑車です。
ひもを引く力はおもりの重さと同じです。
ゆえに、ひもを引く力は100gです。

図２は動滑車です。
ひもを引く力はおもりの重さの半分（1/2）です。
ゆえに、ひもを引く力は50gです。

（２）図１、図２でおもりを10cm持ち上げるとき、ひもをそれぞれ何cm引けばよいですか。

図１は定滑車なので、ひもを引く長さはおもりが上がる長さと同じです。
ゆえに10cmです。

図２は動滑車なので、ひもを引く長さはおもりが上がる長さの２倍です。
ゆえに20cmです。

（３）図１のア点、図２のイ点には、それぞれ何gの力が力がはたらいていますか。

「上に引っ張る力と下に引っ張る力は等しい」の原理を使います。

図１で、定滑車を下に引く力は、おもりの100gとひもを引く力100gの合計の200gです。
アにはたらく力は定滑車を上に引く力であり、下に引く力＝上に引く力なので、アにはたらく力は100+100=200gです。

図２で、動滑車を下に引く力は、おもりの100gだけです。
動滑車を上に引く力は、イの力＋ひもを引く力であり、イの力＝ひもを引く力だから、イの力（＝ひもを引く力）は100÷2=50gです。

（４）図１で、ひもを引く方向をAの向きにかえておもりを持ち上げるとき、ひもを引く力は何gになりますか。

ひもを引く向きをかえても、１本のひもを両方から引く力は等しく、かわりません。
ゆえにAの力は100gです。

次に、複雑な「組み合わせ滑車」の問題を解いてみましょう。

原理１、「１本の糸にはたらく力は等しい」と、
原理２、「上に引っ張る力と下に引っ張る力は等しい」の、
２つさえ上手に使いこなせたら、どんな複雑な滑車の問題もすらすらと解けるようになります。

組み合わせ滑車

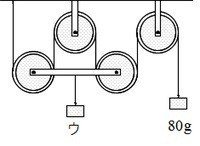
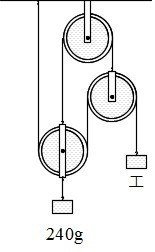
例題２：滑車を組み合わせて、おもりを下げてつり合わせました。あとの問いに答えなさい。ただし、滑車の重さは考えないものとします。

（１）図で、つるしたおもりア、ウ、エはそれぞれ何gですか。

（２）図のイの点にはたらく力は何gですか。

（考え方と解答）

（１）図で、つるしたおもりアは何gですか。

まず、「上に引っ張る力と下に引っ張る力は等しい」から、動滑車を上に引っ張る２つの力は１と１で、下に引っ張るおもりの重さは２です。

おもりの重さ２が500gだから、1の力は、500÷2=250gです。

次に、「１本の糸にはたらく力は等しい」より、アの力は250gです。

（１）図で、つるしたおもりウは何gですか。

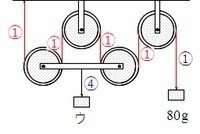
「１本の糸にはたらく力は等しい」から、糸のそれぞれの部分に１を書き込んでおきます。

図を見たらわかるように、おもりのぶら下がった２つの動滑車を４本の糸が上に引いています。
つまり、上に引く力は1+1+1+1=4です。
１にあたる力が80gですから、４にあたる力は80×4=320gです。

「上に引っ張る力と下に引っ張る力は等しい」より、ウのおもりの重さは320gということになります。

（１）図で、つるしたおもりエは何gですか。

「１本の糸にはたらく力は等しい」ことから、エのおもりをさげている糸の３か所に１を書き込みます。

「上に引っ張る力と下に引っ張る力は等しい」ことから、1+1で下に引っ張られている右の動滑車を上に引っ張っている糸に２と書き込みます。
さらに、「１本の糸にはたらく力は等しい」ので、２とつながっている糸の部分にも２と書いておきます。

そうすると、左の動滑車を上に引っ張っている力は、1+2+1=4だとわかります。

「上に引っ張る力と下に引っ張る力は等しい」ので、その動滑車を下に引っ張っているおもりの重さ240gも４の力です。

以上より、１の力は240÷4=60gです。
よって、エのおもりの重さは60gです。

（２）図のイの点にはたらく力は何gですか。

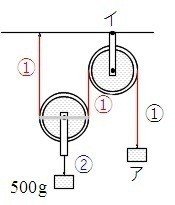
右の定滑車が固定されたイを下に引く力は、1+1=2の力です。

２の力は500gだから、イの力は500gです。

このように、
原理１、「１本の糸にはたらく力は等しい」と、
原理２、「上に引っ張る力と下に引っ張る力は等しい」の、
２つの要領さえ理解できたら、どんな問題でも解けます。

例題３：図１～３の組み合わせ滑車はつりあっています。おもりア～エの重さは何gですか。ただし、滑車の重さは考えないものとします。

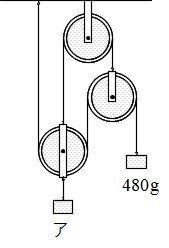
例題３の３

（考え方と解答）

おもりアの重さは何gですか。

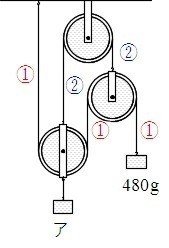
「１本の糸にはたらく力は等しい」ので、480gのおもりを下げている糸の３か所に１を書き込みます。

そうすると、「上に引っ張る力と下に引っ張る力は等しい」から、右の動滑車を上に引っ張る糸の力は２だとわかります。

最後に、左の動滑車を上に引っ張っている力は、1+2+1=4の力です。

１の力が480gだから、４の力は480×4=1920g、アのおもりの重さは1920gです。

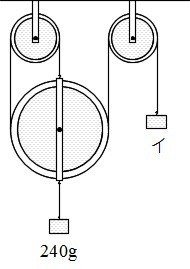
おもりイの重さは何gですか。

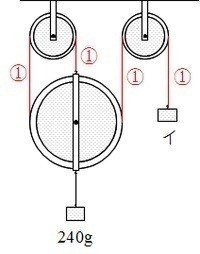
この問題の糸はつながった１本の糸なので、「１本の糸にはたらく力は等しい」より、４か所に１と書き込んでおきます。

左下の動滑車を上に引っ張っている糸は３本だから、動滑車を上に引く力は1+1+1=3の力です。

「上に引っ張る力と下に引っ張る力は等しい」から、動滑車を下に引っ張っているおもりの重さも３にあたる量です。

３にあたる量が240gだから、１にあたる量は240÷3=80gだとわかります。

ゆえに、イの力は80gです。

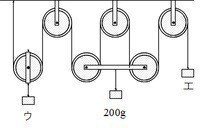
おもりウ、エの重さは何gですか。

まず、「１本の糸にはたらく力は等しい」ので、つながった１本の糸のそれぞれの部分に１を書き込みます。

中央の、２個のくっついた動滑車は４本の糸で上に引っ張られているので、「上に引っ張る力と下に引っ張る力は等しい」より、下に引っ張っているおもりの重さも1+1+1+1=4です。

４の力が200gだから、１にあたる力は200÷4=50gだとわかります。

ゆえに、エの力は50gです。

最後に、ウを考えましょう。

左下の動滑車を上に引っ張っている糸は２本だから、上に引く力は２です。
だから、下に引く力のウも２の力です。

１にあたる力が50gだったので、ウの力は50×2=100gです。

まとめ

組み合わせ滑車の問題では、２つの原理、
「１本の糸にはたらく力は等しい」と、
「上に引っ張る力と下に引っ張る力は等しい」を、
上手に使えばよい。

上手に使うためには、最初、１本の糸のそれぞれの部分に１と書き込めばよい。