
「乱数」とシミュレーション
サイコロを投げたときに出る目の数字は、投げてみないとわかりません。こうした、確率に基づいて不規則に現れる数字のことを「乱数」と言います。乱数の用途は様々ですが、実はコンピューターでは厳密な意味での乱数を生成することが通常は出来ません。そこで、今日はこうした乱数の話と、シミュレーション分野における簡単な応用例についてお話ししたいと思います。
真性乱数と疑似乱数
先程例に挙げたサイコロのように、自然現象の中で生成される乱数は、過去に出た値から将来の値を予測することが出来ません。6面のサイコロなら、ある値のでる確率は1/6ですが、確率は明確でもそこに規則性や再現性はありません。こうした乱数のことを「真性乱数」といいます。
計算機であるコンピューターは、こうした真性乱数を生成することができません。そのため、確定的な計算によって乱数に見立てた数列を生成し、これを真性乱数の代わりとして用いることが一般的となっています。こうした乱数のことを「疑似乱数」と言います。
疑似乱数の性質
一様性
一般に、擬似乱数は生成される数値のばらつきが均一である「一様乱数」であることが殆どです。例えば[1,500]の範囲の乱数を考える場合、1~500までのいずれかの数字が均一の確率で出現するようになっています。周期
簡単に言えば、同じ値が二度目に出たあとは、その後の乱数は過去に出た値が同じ並びで出現するようになります。こうした、同じ値が出るまでの長さのことを乱数の「周期」と言います。
乱数の発生方法
「線形合同法」などの有名なアルゴリズムがありますが、本稿では扱いません。ここでは、例えばエクセルで乱数を生成する方法について考えてみることにします。エクセルの場合は、関数を挿入することで乱数を生成できます。代表的なものにRAND関数とRANDBETWEEN関数があります。
RAND関数を用いると、0以上で1未満の乱数を生成することができます。関数の挿入で、「数学/三角」のカテゴリーにあります。


同じカテゴリーにRANDBETWEEN関数もあります。RANDBETWEEN関数は、整数である範囲の乱数を生成する場合に利用します。


範囲を広げて、コピー&ペーストすると乱数表を作成できます。

乱数の応用例 - モンテカルロ法 -
乱数を用いた計算の応用例としては「モンテカルロ法」が有名です。モンテカルロ法は、乱数を用いて試行を繰り返すことにより、ある問題について近似的な解を求めるなどの目的で利用される計算方法です。
今回、エクセルを用いて簡単にモンテカルロ法で円周率を求めてみます。
半径1の円と、それに接する一辺が2の正方形を考えます。円の中心を原点(0,0)とし、座標は(-1,-1)から(1,1)の範囲の値をとるものとします。

この正方形の中に、乱数を用いて点を打っていき、円の中に入った点の数を数えることとします。今回500個の点を打つことにします。点なので、x座標とy座標で表現し、次のようになります。
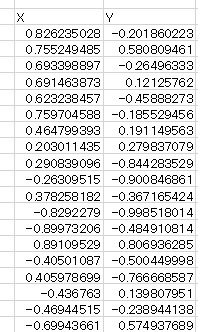
これらの点が円の内側か外側かは、生成した点と円の中心との距離を計算することで調べることができます。<=1であれば、円の内側となります。実際に計算してみます。

<=1となる点の数は、COUNTIF関数で数えることができます。

今回の例では、382個の点が円の内側に入りました。382/500=0.764なので、76.4%が円の内側になります。ここから、正方形の面積「4」の76.4%を計算して、4 x 0.764 = 3.056 となります。この「3.056」が乱数によって求めた円の面積の近似値ですが、円周率の近似値にもなります(円の面積は「半径 x 半径 x 円周率」なので、半径1の円の面積なので円周率と同値になる)。
今回は500点と数が少ないため精度がもう一つですが、点を増やすと精度を上げることができます。
以上が乱数を用いたモンテカルロ法による円周率計算の例となります。
まとめ
乱数は、先日お話しした暗号通信における暗号鍵の生成などにも用いられます。それ以外にも、身近なものでは宝くじなどの賭け事でも乱数は不可欠のものとなっています。
また、機会あればプログラム上での乱数の利用方法や応用例などをご紹介できればと思っています。以上です。お粗末でした。
