
NAND素子の全て
NAND素子は超重要!
今回はNAND素子について取り上げていきます。
論理素子には様々な種類がありますが、特にNAND素子は超重要です!
よくデジタル回路を描く問題で「NAND素子のみを利用して」という制約を目にすると思います。
なぜNAND素子のみを使用した方が良いのかというと、その方が実用上都合が良いためです。
1つにはNAND素子のみの回路は他の素子を利用する場合と比べて、信号の増幅や切り替えを担うトランジスタが少なくて済むからです。
そのためコスパがとても良いです。
もう一つの理由がNAND素子だけを用いて他の素子も全て表現できるからです。
これが超重要なのでぜひ習得してほしいです。
前提知識(ブール代数の公理)
NAND素子で他の素子を作る上で式変形をします。
その際に普通の四則演算とは直感的に異なる計算法則があるので今回用いる巾等法則とドモルガンの法則を紹介します。
・巾等法則
$${x+x=x}$$
$${xx=x}$$
・ドモルガンの法則
$${\overline{x・y}=\bar{x}+\bar{y}}$$
$${\overline{x+y}=\bar{x}・\bar{y}}$$
ドモルガンの法則は有名ですね。
これら2つの計算法則を用いて説明できるので押さえておいてください。
NAND素子の特性
真理値表でNAND素子の特性を確認してみましょう。


NAND素子はANDの否定(NOT)を表しているため、AMD素子の真理値表に対して0と1が反転しています。
式では以下のように表されます。
$${Y=\overline{A・B}(=\bar{A}+\bar{B})}$$
※ドモルガンの法則を用いると上のように変形できますが、今回は上図の形の素子のみを取り上げます。
NANDの真理値表は『A, B共にHighのときにYがLow、それ以外はYがHigh』と覚えると良いでしょう。
NAND素子のみで他の素子を作る
まず簡単なNOT素子から見ていきましょう。
NOT素子
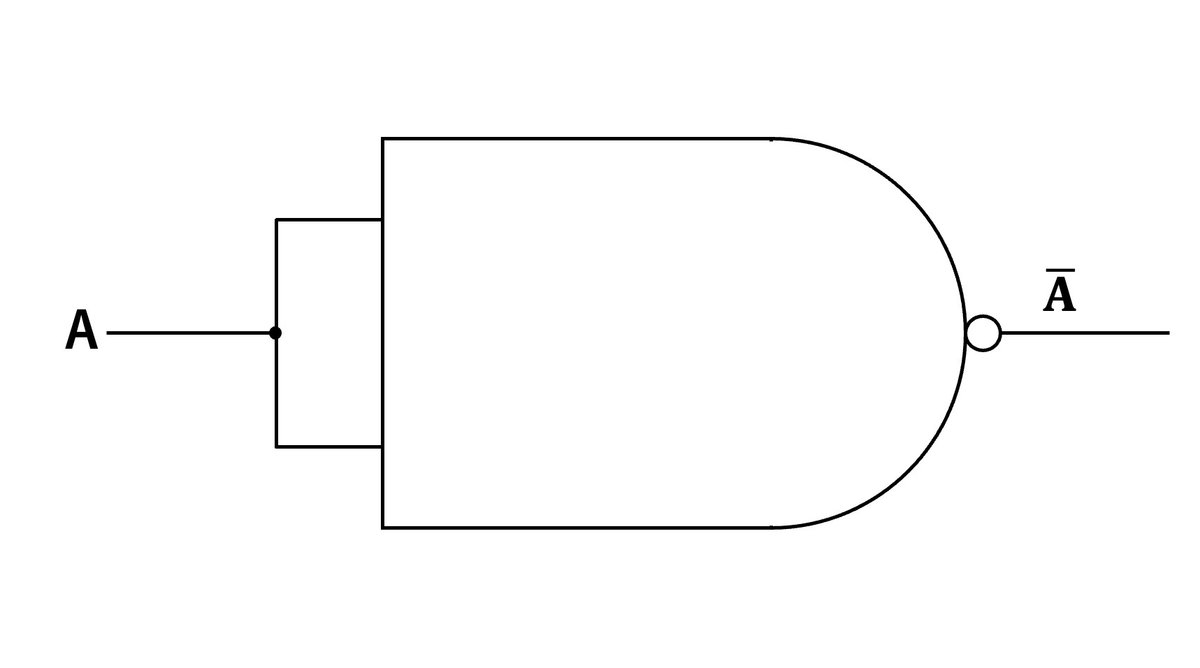
NAND素子の2入力とも同じものを入れるとその否定が出力になります。
先ほど出てきたNAND素子の式において$${A=B}$$とすると、
$${Y=\overline{A・A}=\bar{A}}$$
ここでの式変形で巾等法則を使っていることに注意です。
AND素子
次にAND素子を作っていきます。

先ほどのNOT素子が理解できていれば容易に作れますね。
まずNANDで積の否定を出力して、それを分岐させて2入力に入れると否定されて所望のABが出てきます。
式で捉えると、
$${Y=\overline{\overline{A・B}・\overline{A・B}}=\overline{\overline{A・B}}=AB}$$
となります。
これも巾等法則を使っています。
OR素子
最後にOR素子です。
上の2つと比べると少し複雑かもしれませんが、以下のようになります。

A, Bそれぞれの否定をNAND素子の入力とすれば良いことがわかります。
式変形を見ると、
$${Y=\overline{\bar{A}・\bar{B}}=\overline{\bar{A}}+\overline{\bar{B}}=A+B}$$
となります。
ここで2つ目の等号のところでドモルガンの法則を使っていることに注意です。
練習問題
では試しに上の3つの素子を組み合わせてNOR素子を作ってみましょう。
NOR素子

まずNOR素子とは上のような記号で表され、以下のような真理値表で表される特性を持ちます。

NOR素子はORの否定(NOT)を表しているため、OR素子の真理値表に対して0と1が反転しています。
式では以下のように表されます。
$${Y=\overline{A+B}(=\bar{A}・\bar{B})}$$
ORの真理値表は『A, B共にLowのときにYがHigh、それ以外はYがLow』と覚えると良いでしょう。
NOR素子の特性を理解したところでNAND素子のみでNOR素子を作ってみましょう。
以下解答です。
NORはORの否定なので先ほど示したOR素子の最後にNOTを取り付ければ良いことになります。
以上を踏まえるとNOR素子は以下のように表すことができます。

まとめ
今回はNAND素子を用いて他の素子を表現する方法について学びました。
NOT, AND, ORの3つがNAND素子で作ることができれば他の全ての素子もこれらの組み合わせで代用できます。
実はNOR素子のみでもNOT, AND, ORを作ることができるので興味があればチャレンジしてみてください。
またこれを用いてNAND素子のみでデジタル回路を作図する問題にもトライしてみてください。
