
アナログ信号の離散化
今回はアナログ信号をあるサンプリング周波数で離散化する問題を扱っていきます。
まず例題から確認していきましょう。
例題
アナログ信号$${x(t)=cos(2000πt+ \frac π 4)}$$をサンプリング周波数$${f_s=}$$8 kHzで離散化すると離散信号$${x[n]}$$を得た。
以下の問いに答えよ。
(1)$${x[n]}$$は?
(2)$${x[n]}$$の周期は?
(3)信号を0.1 msだけ遅らせたとき、位相変化は?
前提知識
今回の問題を解くのに必要な前提知識をまとめました。
・アナログ信号の離散化
アナログ信号は時間tに依存する三角関数でよく表されます。
この信号をある周波数$${f_s}$$で離散化するというのは、信号を$${f_s}$$個に分割するということに相当します。
これは$${f_s=\frac 1 {T_s}}$$という関係からも明らかで問題を解く際には、
$${t→\frac n {fs}}$$と置き換えれば良いことになります。
・信号の周期
アナログ信号$${x(t)}$$を
$${x(t)=cos(\alpha t+ \beta)}$$と表すとき周期$${T}$$は、
$${T=\frac {2\pi} {\alpha}}$$で表されます。
例題の解説
(1)
まず$${f_s=}$$8 kHzなので離散化するには
$${t→\frac n {8000}}$$とすれば良いので離散信号は、
$${x[n]=cos(\frac \pi {4}n+\frac \pi {4})}$$
となります。
(2)
離散信号の周期は、
$${T=\frac {2\pi} {\frac \pi {4}}=8}$$
となります。
(3)
信号を0.1 ms遅らせるというのは時間について言っているのでアナログ信号$${x(t)}$$において、
$${t→t-0.0001}$$と置き換えれば良いです。このとき、
$${x(t-0.0001)\\=cos(2000π(t-0.0001)+ \frac π 4)\\=cos(2000\pi t+\frac π 4-0.2π)}$$
となるので位相変化は、
$${-0.2π}$$
と求められます。
練習問題
アナログ信号$${x(t)=2cos(800πt+ \frac π 4)+cos(1600πt)}$$をサンプリング周波数$${f_s=}$$3200 Hzで離散化すると離散信号$${x[n]}$$を得た。
以下の問いに答えよ。
(1)$${x[n]}$$は?
(2)$${x[n]}$$の周期は?
今回は二つの異なる波の合成波がアナログ信号をして与えられていますね。
でもやるべきことは例題と一緒です。
例題を参考にトライしてみましょう。
以下解答です。
練習問題の解答
(1)
まず$${f_s=}$$3200 Hzなので離散化するには
$${t→\frac n {3200}}$$とすれば良いので離散信号は、
$${x[n]=cos(\frac \pi {4}n+\frac \pi {4})+cos(\frac \pi {2}n)}$$
となります。
(2)
離散信号の周期についてですが、例題と違うのは合成波であることだけです。
実際に周期の異なる波を描いてみるとわかりやすいですよ。
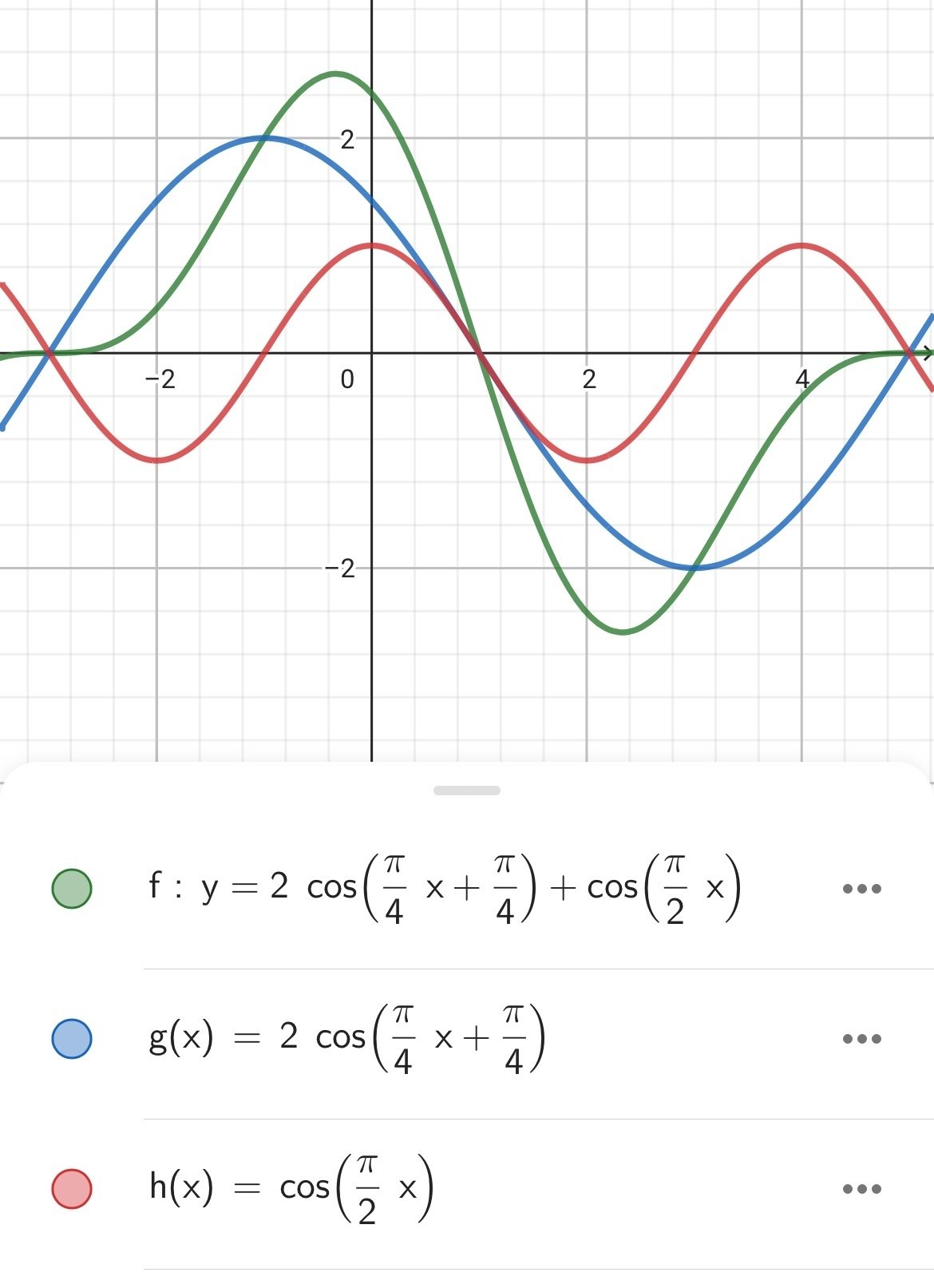
"GeoGebra"というソフトにグラフを描いてもらいました。
緑が合成波を、青は振幅が2の方の波を、赤は振幅が1の方の波を表しています。
グラフを見ると緑の1周期分の中に青が1周期分、赤が2周期分入っていることがわかります。
このことから合成波の周期は青の波の周期に依存することになります。
実際に確認で2つの波の離散信号における周期を求めてみると、
・青:$${T_{blue}=\frac {2\pi} {\frac \pi {4}}=8}$$
・赤:$${T_{red}=\frac {2\pi} {\frac \pi {2}}=4}$$
となることから合成波の周期は8と求められました。
つまり合成波の周期は2つ(以上)の波の周期の最小公倍数で求められると言えます。
まとめ
今回はアナログ信号の離散化について学びました。
複雑な計算が必要ないので簡単だったと思います。
ただし合成波の周期を求めるときは注意してください。
次はサンプリング定理の問題にチャレンジしてみると良いかもしれません。
