
Python-Control 制御工学 2次系ステップ応答を matplotlib で出力
Python-Control を使った制御工学に取り組んでいます。最終的にはPID制御を用いたフィードバック制御系の設計に活用できればいいなと考えています。本記事では、2次系のステップ応答波形を matplotlib で出力してみます。また、パラメータを変化させた比較波形も出力してみます。
環境
・windows 10(64bit)
・Visual Studio Code 1.45.1
・Python 3.8.2(32bit版)
2次系 ステップ応答
2次系のステップ応答を導出します。s領域における2次系の伝達関数は次式になります。この伝達関数モデルを Python で作成し、パラメータを与えてステップ応答の波形を matplotlib で出力します。
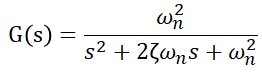
Python ソースコード
まず、演算に必要なライブラリをインポートします。そして、defを使って関数 tf_2nd_order( ) を定義しています。この関数は第一引数に ζ 、第二引数に ωn を与えれば、計算結果として2次系の伝達関数が出力されます。ステップ応答を出力する際は、numpy の関数 linspace( ) を使って時間のパラメータを作成しています。下記のコードでは0から2まで1000分割した値になります。伝達関数モデルと時間を関数 step( ) の引数に与えてステップ応答の出力を得ます。
# 数値演算ライブラリ
import numpy as np
# 制御工学ライブラリ
from control import matlab
# グラフ描画
from matplotlib import pyplot as plt
# 2次系伝達関数モデル作成の関数
def tf_2nd_order(zeta, wn):
num = [wn*wn]
den = [1, 2*zeta*wn, wn*wn]
G = matlab.tf(num, den)
return G
# 伝達関数モデル作成
G2nd = tf_2nd_order(0.6, 10.0)
# 伝達関数モデル出力
print(G2nd)
# ステップ応答
t = np.linspace(0, 2.0, 1000)
(output, t) = matlab.step(G2nd, t)
# 出力パラメータ
plt.plot(t, output)
plt.axhline(1.0, ls=":", color="blue")
# グラフ表示設定
plt.rcParams['font.family'] = 'Times New Roman' # 全体のフォント
plt.title('2nd order step', fontsize=10) # グラフタイトル
plt.xlabel('time [sec]', fontsize=10) # x軸ラベル
plt.ylabel('Output', fontsize=10) # y軸ラベル
plt.xlim([0, 2.0]) # x軸範囲
plt.ylim([0, 1.2]) # y軸範囲
plt.tick_params(labelsize = 10) # 軸ラベルの目盛りサイズ
plt.tight_layout() # ラベルがきれいに収まるよう表示
plt.grid() # グリッド表示
plt.show() # グラフの表示結果
100
----------------
s^2 + 12 s + 100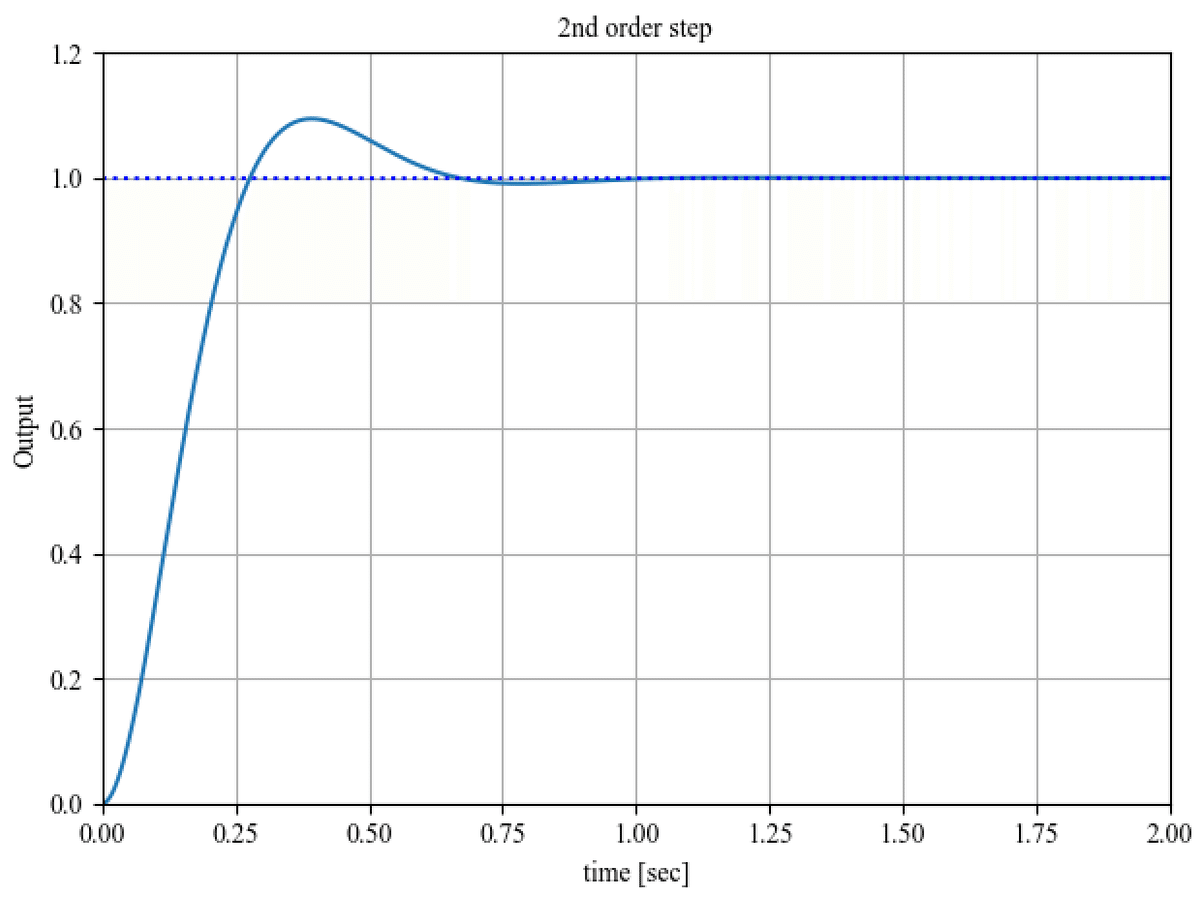
パラメータを変えて波形の振動性を比較する
次に、パラメータを変化させてステップ応答波形を比較してみます。変化させるパラメータは ζ とします。ζ を変化させると波形の振動が変化します。1< ζ のときは非振動的な波形になります。0 ≦ ζ ≦ 1のときは振動的な波形になります。ζ が小さくなるにつれて振動性が強くなります。また、ωn が大きくなると応答が早くなり、ωn が小さくなると応答が遅くなります。今回は振動性の比較をしたいので ωn は一定の値とします。
Pythonソースコード
行数が増えてきたので、先ほどとは少し書き方を変えてみました。固定値のパラメータはソースコードの初めに大文字で定義するように書いています。以降は固定値パラメータに値は代入しないようにします。ζ を変化させたステップ応答波形を出力するため、for文を使って ζ の値を変化させます。数式は ζ=i×0.2 となっており、iは0から10まで変化するので、ζは0から2.0まで、0.2間隔の値となります。for文で回した後に、グラフ表示設定を行い、最後にグラフを表示させます。おまけに、ボード線図も同様にして出力します。
#------------ ライブラリインポート ------------#
# 数値演算ライブラリ
import numpy as np
# 制御工学ライブラリ
from control import matlab
# グラフ描画
from matplotlib import pyplot as plt
#------------ 固定パラメータ ------------#
# ステップ応答時間設定
TIME_START = 0.0
TIME_END = 2.5
TIME_STEP = 1000
#------------ 関数定義 ------------#
# 2次系伝達関数モデル作成の関数
def tf_2nd_order(zeta, wn):
num = [wn*wn]
den = [1, 2*zeta*wn, wn*wn]
G = matlab.tf(num, den)
return G
#------------ Main ------------#
# 伝達関数モデル作成 & ステップ応答導出
for i in range(0, 11):
param_zeta = round(i*0.2,1)
param_wn = 10.0
G2nd = tf_2nd_order(param_zeta, param_wn)
# ステップ応答
t = np.linspace(TIME_START, TIME_END, TIME_STEP)
(output, t) = matlab.step(G2nd, t)
# 波形出力パラメータ
# (ls:線種, lw:線太さ, alpha:透過度, color:色指定, marker:マーカー形状指定, ms:マーカーサイズ, label:凡例名)
label_name = "ζ = " + str(param_zeta)
plt.plot(t, output, alpha=0.7, label=label_name)
# 収束値を点線表示
plt.axhline(1.0, ls=":", color="blue")
# グラフ表示設定
plt.rcParams['font.family'] = 'Times New Roman' # 全体のフォント
plt.legend(loc="upper right",fontsize=8) # 凡例の表示(2:位置は第二象限)
plt.title('2nd order step', fontsize=10) # グラフタイトル
plt.xlabel('time [sec]', fontsize=10) # x軸ラベル
plt.ylabel('Output', fontsize=10) # y軸ラベル
plt.xlim([0, TIME_END]) # x軸範囲
plt.ylim([0, 2.0]) # y軸範囲
plt.tick_params(labelsize = 10) # 軸ラベルの目盛りサイズ
plt.tight_layout() # ラベルがきれいに収まるよう表示
plt.grid() # グリッド表示
plt.show() # グラフの表示
# 伝達関数モデル作成 & ボード線図
for i in range(0, 11):
param_zeta = round(i*0.2,1)
param_wn = 10.0
G2nd = tf_2nd_order(param_zeta, param_wn)
# ボード線図作成
label_name = "ζ = " + str(param_zeta)
matlab.bode(G2nd, label=label_name)
# グラフ表示設定
plt.legend(loc="upper right",fontsize=8) # 凡例の表示(2:位置は第二象限)
plt.show() # グラフの表示結果
ステップ応答波形から、1< ζ のときは非振動的な波形となり、0 ≦ ζ ≦ 1のときは振動的な波形になっていることが分かります。また、ζ が小さくなるにつれて振動性が強くなっています。2次系のシステムでオーバーシュートさせたくない場合は、1 < ζ で設計するのが良さそうです。ボード線図から、-40dBで減衰し、位相は-180° になることが分かります。ζ が大きいほど、位相は緩やかに低下していきます。


おわりに
本記事では2次系の伝達関数のステップ応答波形を導出し、1< ζ のときは非振動的な波形となり、0 ≦ ζ ≦ 1のときは振動的な波形になっていることが分かりました。この結果の展開例として、システムのフィードバック制御系を構築した際、その閉ループ伝達関数が2次系になるとき、ステップ入力信号に対して出力を振動させたくなければ、1< ζ で設計すれば良いということが分かります。引き続き、他の記事でも Python-Control を使って色々なことをやっていきたいと思います。何か不備や不明点がありましたらコメントをして頂けると嬉しいです。
いいなと思ったら応援しよう!

