
3球目攻撃を物理的に考察してみる
こんにちは、トモヒトです。
今回は、3球目攻撃を物理的に考察してみます。
相手に反撃されないサーブ
相手に反撃されないサーブと考えると、「相手に踏み込まれないサーブ」と考えられます。
サーブのシミュレーションは、下のコードを使用します。
今回は、「相手がベースラインと平行にリターンに動いた場合、横へ2m以上(アレーよりも外側)で返球するサーブ」と仮定します。
今回の例では、サーブがベースラインを通過したとき、x>=6を満たすサーブが、この仮定に該当します。
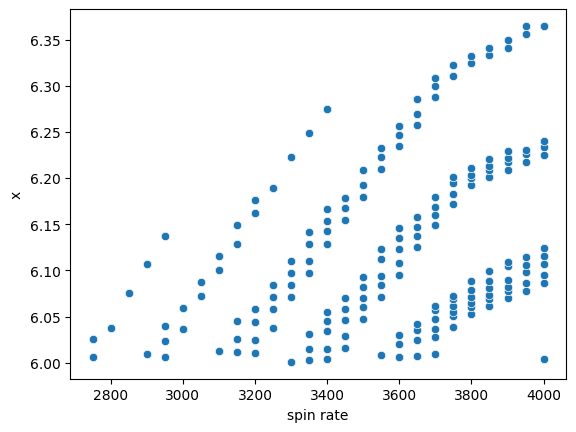
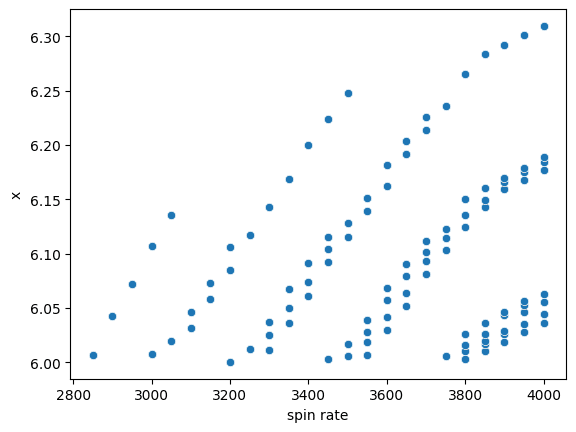
横方向のリターン位置とサーブの到達時間の関係は、次のグラフのとおりです。
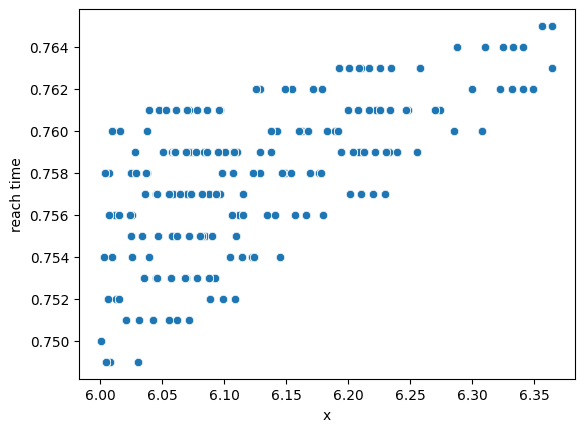

レシーバーの合理的待機位置へ戻るリカバリー所要時間
次は、レシーバーが合理的待機位置に戻るのに必要なリカバリー所要時間を算出します。
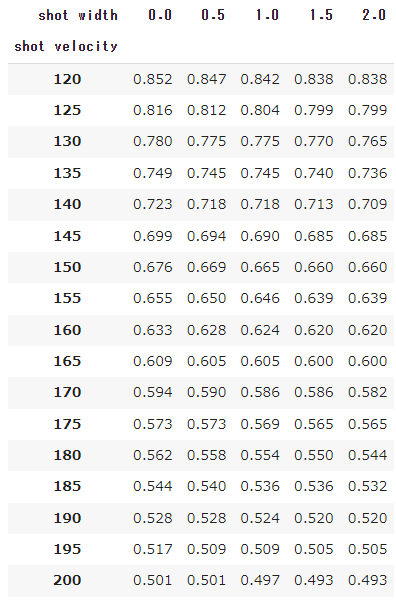
サーバーの3球目のショットスピード/ヒッティングポジション別合理的待機位置
まずは、サーバーの3球目のショットスピード/ヒッティングポジション別合理的待機位置を見ていきます。
x, y:サーバーのヒッティングポジション
x=アドサイドのシングルスサイドラインからの距離
y=ベースラインを0とし、ネット方向を正としたときの前後の位置サーバーの3球目の打点の高さは、1.2mで計算
px:レシーバーの合理的待機位置(横方向の位置)
デュースサイドのシングルスサイドラインからの距離fl:合理的待機位置からの最大移動距離
一番外側のショットに対して移動する距離を表すレシーバーの合理的待機位置の縦方向(ネット方向)に関しては、ベースライン後方1mの位置を想定


レシーバーの合理的待機位置へのリカバリー所要時間
次は、レシーバーの合理的待機位置へのリカバリー所要時間を算出します。
今回は、以下の想定で話を進めていきます。
リターン後、リカバリーのスタートまで0.1秒要する
前後の位置は、リターン時はベースラインの延長線上、合理的待機位置はベースライン後方1mの位置とする
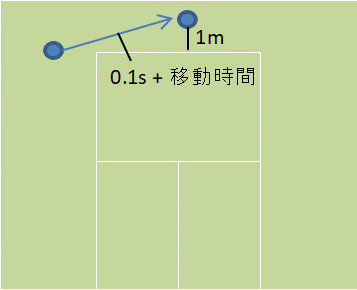
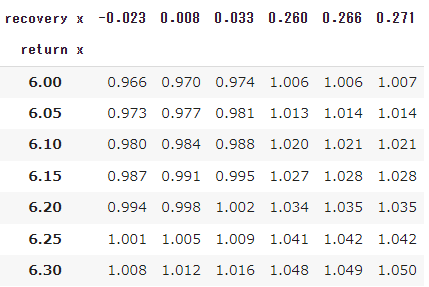
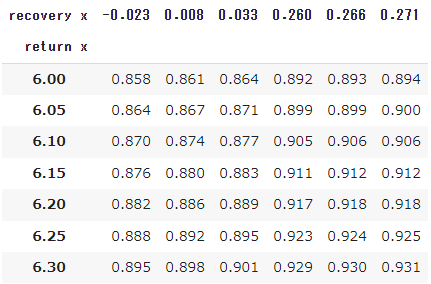
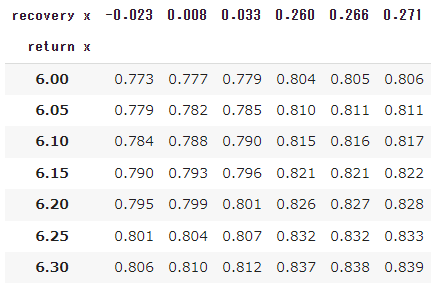
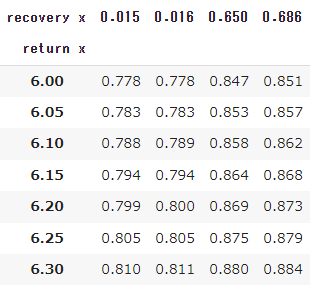
上の「サーバーの3球目のショットスピード/ヒッティングポジション別合理的待機位置」をもとに、リカバリー所要時間を算出してみます。
下表では、
return x=リターン時の横方向の位置(センターマークを0mとする)
recovery x=合理的待機位置の横方向の位置(センターマークを0mとし、リターンと逆サイドを正とする)
※recovery x + (8.23/2) = px
を表します
レシーバーのスプリントスピード=7m/sのとき
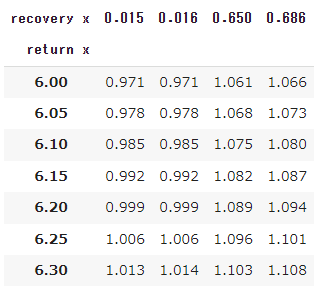
レシーバーのスプリントスピード=8m/sのとき
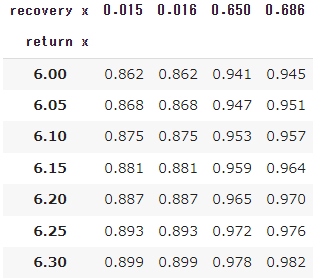
レシーバーのスプリントスピード=9m/sのとき
3球目のショットの条件
最後は、3球目にはどのようなショットが必要かを考えてみます。
ポジション・ショットスピード別のショット到達時間
まずは、ポジション別のショット到達時間をまとめておきます。
これは、3球目のショットがベースライン後方1mラインを通過する時間を表しています。
センターマークから0.115m/ベースライン上の地点
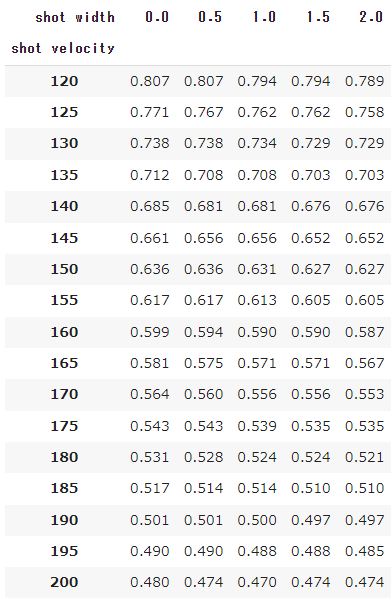
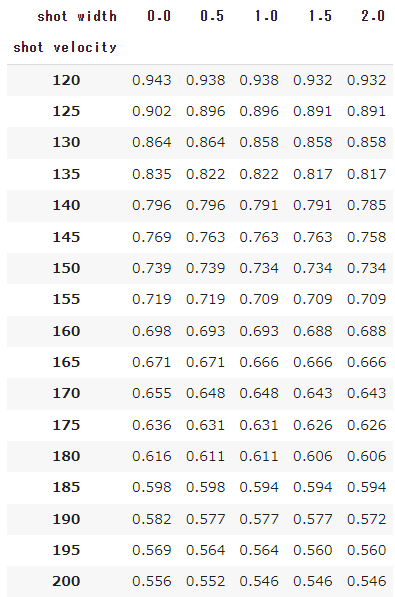
センターマークから0.115m/ベースライン内1mの地点
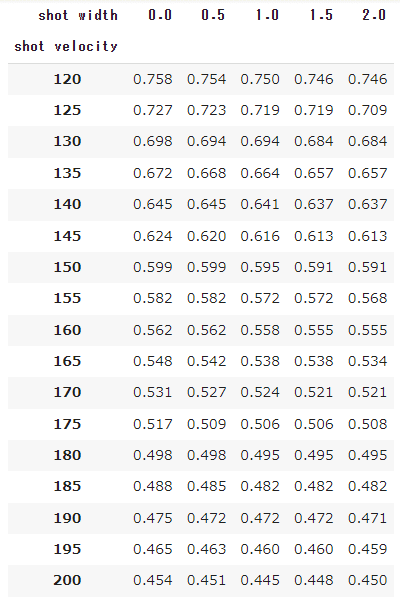
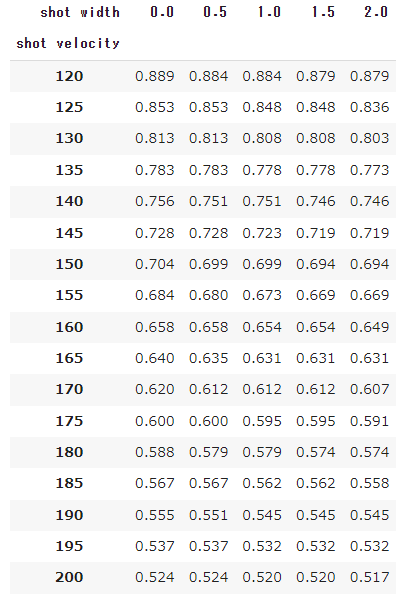
センターマークから0.115m/ベースライン内2mの地点

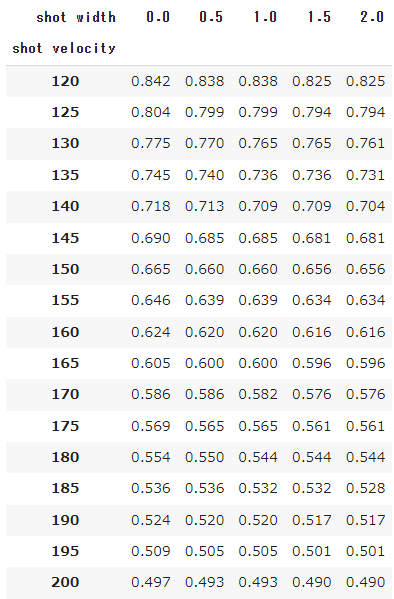
センターマークから1.115m/ベースライン内上の地点
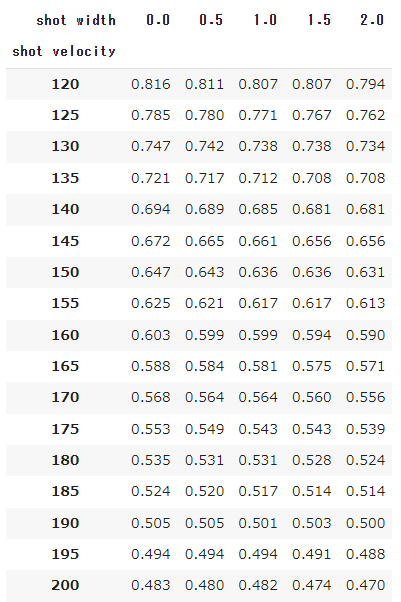
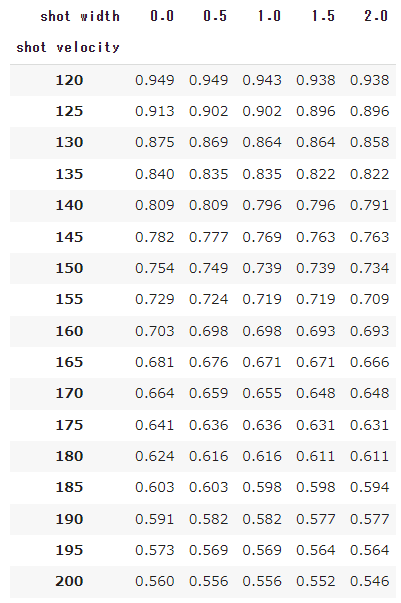
センターマークから1.115m/ベースライン内1mの地点
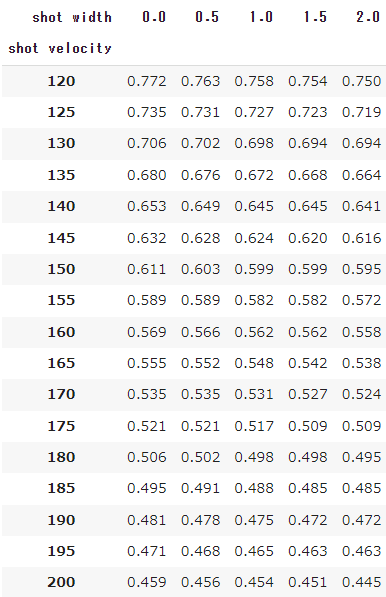
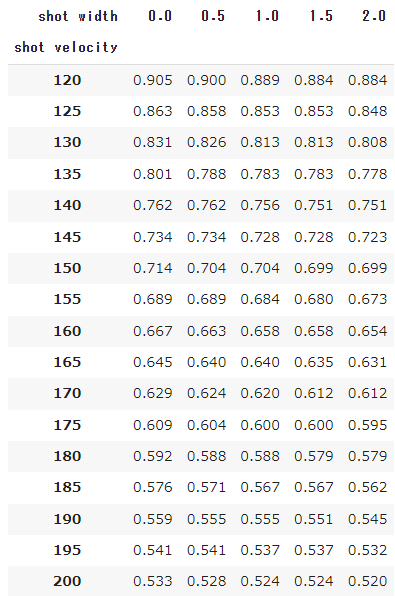
センターマークから1.115m/ベースライン内2mの地点
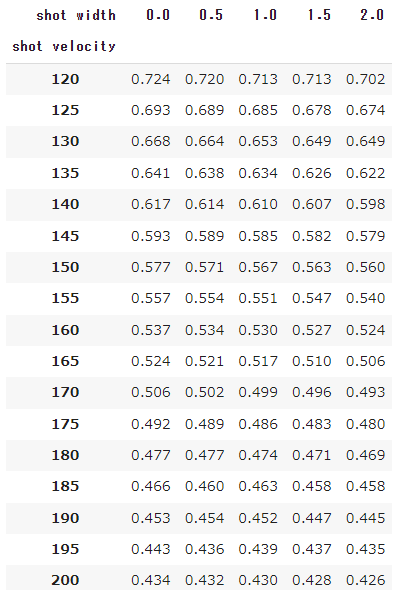
相手が合理的待機位置にいるケースと、オープンコートができている(合理的待機位置に戻り切れていない)ケースに分けて考えてみます。
3球目攻撃(相手は合理的待機位置にいる)
相手が合理的待機位置にいる場合、「相手の合理的待機位置からヒッティングポジションまでの移動にかかる時間が、ショットの到達時間を上回る」ケースを考えます。
ここでは「サーバーの3球目のショットスピード/ヒッティングポジション別合理的待機位置」のショット到達時間別のflの値を使います。
つまり、
$$ \frac {必要な移動距離 - リーチの長さ} {ショット到達時間 - 反応時間} > スプリントスピード$$
となれば、3球目攻撃が成立したとみなします。
例えば、3球目をセンターマークから1.115m/ベースライン内2mの地点から130km/hのショットで打つ場合、ショット到達時間が0.95秒のときfl=5.729mとなります。
リーチの長さを1m、反応時間を0.2秒と仮定すると、必要なスプリントスピードは
$$\frac {5.729 - 1} {0.95 - 0.2} = 6.305〔m/s〕$$
となります。
同じ位置から160km/hのショットで打つ場合、ショット到達時間が0.75秒のときfl=4.807mとなります。
リーチの長さを1m、反応時間を0.2秒と仮定すると、必要なスプリントスピードは
$$\frac {4.807 - 1} {0.75 - 0.2} = 6.922〔m/s〕$$
となります。
これをみると、相手が合理的待機位置に戻っている場合、相手のスプリントスピードが7m/sと仮定しても、3球目を160km/hよりも速く打つ、またはベースライン内2mよりも前で打つことができなければ、3球目攻撃は成立しないとなります。
3球目攻撃(オープンコートができている)
次は、オープンコートができているパターンについて考えてみます。
このケースは、3球目のショットごとに、相手がどの位置にいれば相手が追いつけないのかを見てみます。
ここでは、以下の想定で考えます。
相手は、ベースライン後方1mの位置にいるとする
相手は、オープンコートを埋める選択肢に絞っている
=>3球目を打った瞬間にスタートを切ると仮定(=反応時間0秒)相手のリーチは1mと仮定
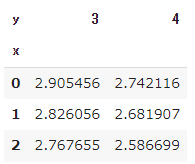
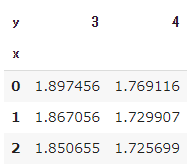
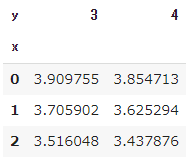
3球目はミドルクロスへのショットとし、ベースライン後方1mラインへのショット到達時間が、レシーバーのスプリント時間を上回れば、3球目攻撃が成立したとする
リターンしたサイド側に、センターマークから何m以上離れていれば、3球目が決まるかを見ていきます。
ここでは、レシーバーのフットワークスピードを7m/sと仮定します。
ミドルクロスへの3球目
ディープクロスへの3球目

まとめ
今回は、3球目攻撃を物理的に考察してきました。
3球目攻撃を成功させるには、3球目のショットスピードとコースから、レシーバーがどの位置にいれば決まるのかから逆算することがポイントです。
そして、その位置に残すためには、サーブでどのくらい相手をコート外に動かす必要があるかをイメージしてサーブを打つ必要があります。
最後までお読みいただきありがとうございました。
ご意見ご感想あれば、コメントにお願いします。
