たすきがけない因数分解

特に書くネタもなかったので。

たすきがけの因数分解を、たすきがけを用いないで解く手法です。
本質的に同じようなことをやっている人はいますが、
見栄えはこちらのほうがいいと思います。

解説

たすきがけとかいう概念も生じさせないほど簡単な例題はこちら。

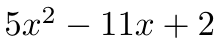
①　２次の係数をかけた式をつくり、辻褄合わせの分数をかける。
　　定数項だけ暗算する。暗算できなければしない。

②　かっこ内を因数分解する。苦手な人は変数変換する。

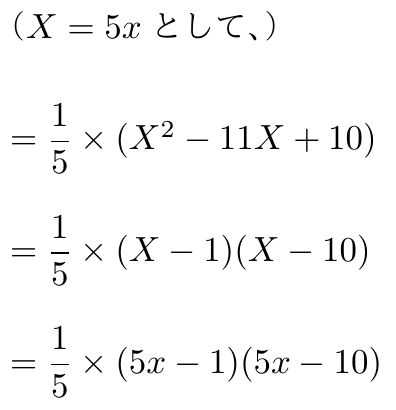
③　さらに、かっこ内を因数分解する。
　　大抵、辻褄合わせの分数で約分できる。

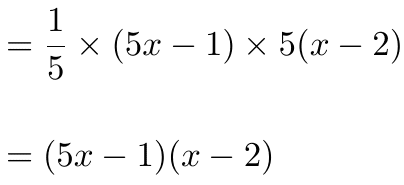
大変なパターン

某動画から拝借した例題はこちら。

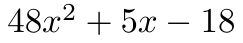
①　２次の係数をかけた式をつくり、辻褄合わせの分数をかける。
　　定数項だけ暗算する。暗算できなければしない。

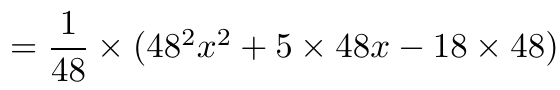
②　かっこ内を因数分解する。苦手な人は変数変換する。

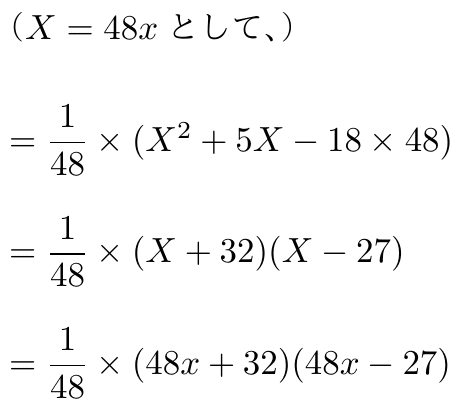
（余談１）
M+N=5、MN=-18×48を満たす二整数M, Nを求めたいわけだが、
和が奇数なので、二整数は偶数と奇数で構成される。
奇数側の素因数には2が含まれないので、
-18×48の素因数に含まれる2は、すべて偶数側の素因数に含まれる。
ここで、-18×48の素因数に含まれる2をすべて抜き出すと、
32を抜き出すことができ、-9×3が残る。
したがって、偶数側をMとすれば、整数mを用いてM=32mと書けるので、
32m+N=5、mN=-9×3を満たす二整数m, Nを求めればよい。

（余談２）
M=32mより、Mの絶対値は32以上であり、
mN=-9×3より、Nの絶対値は27以下であるから、
Mの絶対値とNの絶対値の差は5以上である。
ここで、M+N=5より、Mの絶対値とNの絶対値の差は5である。
したがって、32mの絶対値は32、Nの絶対値は27となる。
※本来であれば、m, Nを調整して絶対値差を合わせにいく。

③　さらに、かっこ内を因数分解する。
　　大抵、辻褄合わせの分数で約分できる。

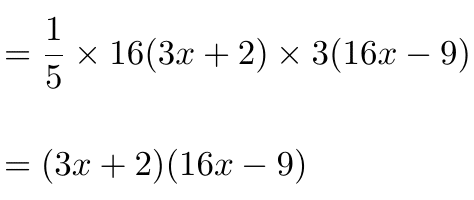
結局はただ

２次項の係数が1でない２次方程式を、２次項の係数が1である２次方程式に帰着させているだけです。