
特別区の暗号問題を解くための2つの考え方
こんにちは!
特別区の受験に特化したオンライン予備校「トクヨビ」の代表をしている荒川です。
今回のテーマは「特別区の暗号問題を解くための2つの考え方」ということで、特別区に合格したい人に向けて、判断推理で出題される暗号問題を解くためのコツを解説していきます。
先日、僕の公式LINEにこのような質問が来ました。
「判断推理でもっと点数が取りたいです。特に暗号問題が解けないことが多いので、何かポイントがあれば教えていただけないでしょうか?」
という質問です。
特別区の教養試験では、採用区分に関わらず判断推理の2問目に暗号問題が出題されます。
あなたは特別区の暗号問題を解く際に、
「どこから手を付ければいいのか分からない」
「解くのに毎回時間がかかる」
「こんな暗号、解ける人いるの?」
と悩んだことはないでしょうか?
そこで今回は、特別区の暗号問題を解くための2つの考え方をお伝えします。
たしかに暗号問題の中には、難しくて短時間で解きにくいものも存在します。
とはいえ、解くための基本的な考え方は今回お伝えするたった2つです。
そのため、この考え方を知っているか知らないかで、他の受験生と大きな差がつきます。
それに択一試験は時間との勝負でもあるので、解き方のパターンを覚えていないと一問解くのにものすごい時間がかかってしまいます。
これでは合格点を取ることはできません。
でも安心してください。
今回説明する暗号問題を解く際の考え方を知ってしまえば、素早く暗号を解読できるようになります。
僕は教養試験の中でも判断推理・数的処理のような、いわゆる算数や数学の問題が一番得意ですし、分かりやすく教えられる自信があります。
過去にYouTubeで教養試験の解説動画を公開していたのですが、当時の受験生からも「荒川さんの解説動画のおかげで教養試験の点数が上がりました!」という声をたくさんいただきました。
また、僕はこれまでにⅠ類採用と経験者採用の過去問をそれぞれ10年以上、つまり合計で20年以上解いてきましたので、暗号問題に共通するポイントを熟知しています。
あなたも今回の考え方を覚えておくだけで、今よりも簡単に暗号問題が解けるようになります。
「暗号問題の正答率を上げたい!」
「解く際に必要な考え方を知りたい!」
「短時間で暗号解読できるようになりたい!」
とあなたが思っているのであれば、今回の内容を学ぶと今までよりラクに解けるようになるので、ぜひ最後までご覧ください。
暗号問題を解くための2つの考え方

今回は実際に過去問を使いながら解説していきます。
早速ですが、こちらの問題をご覧ください。

一度読むのをやめて、解いてみてください。
(考え中・・・。)
どうでしたか?解けましたでしょうか?
この問題を解く際にポイントとなるのは、アルファベット順で考えるということです。
つまり、AからZまでを書き出して規則性を考えればOKです。
今回の問題は、AからDの4つの規則性がすぐに分かります。
このように色を付けてみると、より分かりやすくなるはずです。

Aが「上上上」、Bが「上上中」、Cが「上上下」、Dが「上中上」となっています。
つまり、AからCに進むにつれて、一番右の漢字が「上→中→下」と変化していき、一番右の変化が終わると真ん中の漢字が「上」から「中」に変わります。
アルファベット順で考えると、問題文で与えられているアルファベットはこのように対応することが分かりました。

ここまで来ると、後はそこまで難しくありません。
EとFはこのようになります。

G・H・Iは真ん中が「下」になりますよね。

この時点で、真ん中と右側の漢字は「上→中→下」とすべて変化しました。
残りは左側の漢字が変化すればいいですよね。
つまり、J以降は左側の漢字が「中」になります。
こうです。

Rまで書いてみると、左側が「中」になるパターンはすべて書き出したことに気づけます。
最後は左側の漢字を「下」にすればOKです。
つまりこうなります。

これで全てのアルファベットの対応表が完成しました。
問題では、「下上上、上下中、中中下、中下上」と表されるのはどれかと聞かれているので、「SHOP」になりますね。
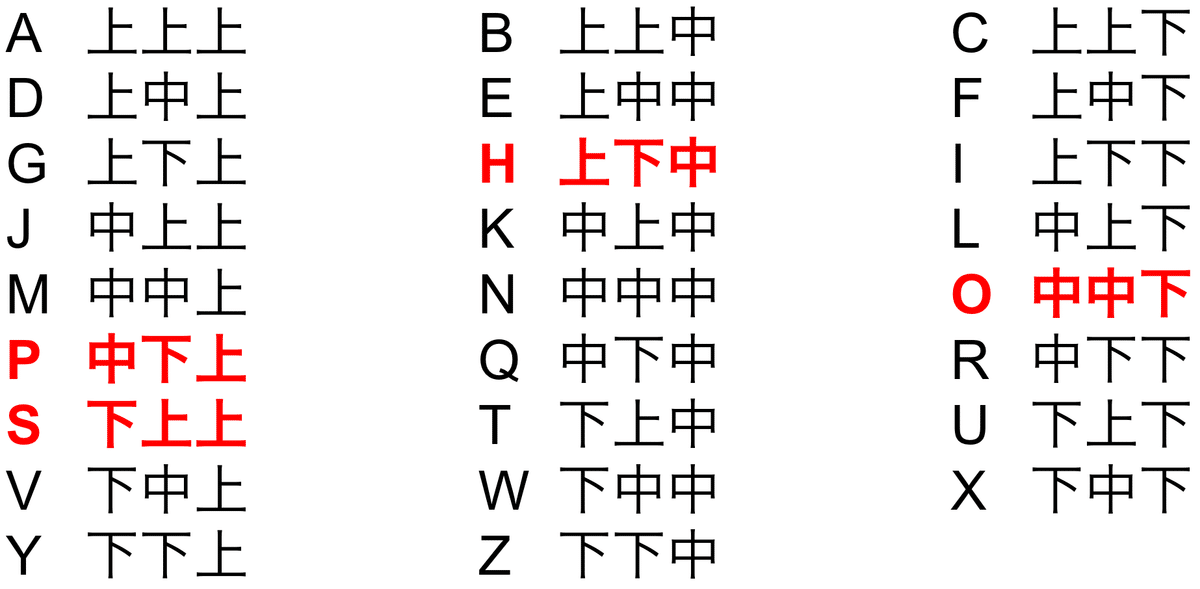
これが正解です。
このように、今回の問題はアルファベット順で考えることで規則性を見つけることができました。
続いて、こちらの問題をご覧ください。

一度読むのをやめて、解いてみてください。
(考え中・・・。)
どうでしたか?解けましたでしょうか?
この問題を解く際にポイントとなるのは、あいうえお順で考えるということです。
つまり、このようなひらがな表を余白に書きましょう。

今回の問題は、カタカナ1文字に対して割り算の式が1つ対応していることにはすぐに気づけるはずです。
つまり、「タ」が「4÷1」、イが「2÷1」のようになっています。
そして、今回の割り算はすべて割り切れるのもポイントです。
それぞれの割り算の答えはこのようになります。

ここで注目してほしいのは、答えが1になった「タ」と「ア」と「カ」の3つです。

これらは、すべてひらがな表の1行目の文字になっています。
同様に考えると、答えが2になっている「イ」と「リ」はひらがな表の2行目の文字になっていることに気づけます。

つまり、割り算の答えがひらがな表の行と一致するというわけです。
もう一度ひらがな表を考えてみると、このようになります。

では、列についても考えてみましょう。
こうなります。

この列の数字が問題文のどこと対応しているかを見てみると、実は「割る数」と一致していることが分かります。

これで規則性が分かったので、暗号を解いてみましょう。
「ラオス」の「ラ」は1行目の9列目なので、「◯÷9=1」という式が成り立ちます。

◯に入るのは9なので、「ラ」は「9÷9」です。
続いて「オ」は5行目の1列目なので、「◯÷1=5」が成り立ちます。

◯に入るのは5なので、「オ」は「5÷1」です。
最後の「ス」は3行目の3列目なので、「◯÷3=3」が成り立ちます。

◯に入るのは9なので、「ス」は「9÷3」です。
よって「ラオス」は「9÷9、5÷1、9÷3」になります。
このようにあいうえお順で考えることで暗号を解読できました。
実は、特別区の暗号問題のほとんどは、今回の説明のように「アルファベット順」もしくは「あいうえお順」で解くことができるのです。
これさえ知っておけば、暗号問題を解読するためのポイントに気づきやすくなるので、解くスピードも自然と上がります。
ただし、たまに「アルファベット順」と「あいうえお順」のどちらで考えても解けない場合もあるので、その場合は潔く他の問題を優先的に解くことをおすすめします。
解けそうにない問題に時間を使いすぎるのはもったいないです。
ですが何度も言うように、ほとんどの暗号問題は今回説明したいずれかの方法で解読できるので、過去問を解く際にはぜひ活用してください。
まとめ

ということで今回は、「特別区の暗号問題を解くための2つの考え方」について解説しました。
暗号問題を解く際には、「アルファベット順」もしくは「あいうえお順」を使って解読できないかを考えましょう。
特別区の暗号問題は、これら2つの考え方を使えば、ほぼ全ての問題を解くことができます。
1度読んでも分からなかった方は、今回解説した問題を解き直してみてください。
最後までご覧いただき、ありがとうございました。
もしこの記事が少しでも良かったと思ってくれた方は、いいね(♡マーク)や𝕏での共有をよろしくお願いします。
【公式LINE】
公式LINE登録者限定の無料Zoom相談会などを開催中です!
📌Ⅰ類採用向け
📌経験者採用・氷河期採用向け
【公式HP】
元特別区職員が教える特別区受験に特化したオンライン予備校です。
1週間の無料体験も可能ですので、特別区になんとしても合格したい方は是非お申し込みください。
【YouTube】
今回の内容を動画で学びたい方はこちらをご覧ください!
