
【Aidemynote】RとPythonで、W杯のサッカー選手は体格がよいほど、走れないのか?を分析してみた。
ちょっと前までW杯で盛り上がっていましたね!
佐々部考紀さんというトレーナー兼研究者の方が、サッカー選手が「筋肉をつけすぎると走れなくなる説」を検証するために、日本、ベルギー、フランス代表の選手の体格とW杯の試合での90分あたりの走行距離を比較しておられましあ。
分析の対象は興味深く、データもW杯に出た選手のものでタイムリーで、非常に面白い。ただ一つ疑問なのは体格を(身長-体重)で計算しちゃったこと!
本当にこれでよいのか?これ多分イメージしやすいためにわかりやすい指標にされたんだと思いますが、本来は
多変数の回帰分析
なので、重回帰分析をすべきな気がして、あと今、仕事のために多変量解析を復習しないといけないところなので分析したくなりました!
重回帰分析は以下の二つのサイトがわかりやすく書いてあります。
特に下の方はRのコードがいくつかのっているので有用です。
pythonでもやりたかったんですが、ちょっと忙しかったので、佐々部さんのツィートからデータ(もとは朝日新聞、および)を拝借して、まずは慣れているRで!
x1 <- read.table(file="football.txt", header=T, sep='\t')
reg <- lm(Run~Hight+Weight, data=x1)
summary(reg)データ読み込んで、回帰分析すると
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 15.47234 5.27500 2.933 0.00676 **
Hight -0.02119 0.03902 -0.543 0.59155
Weight -0.02375 0.03132 -0.758 0.45486
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.8395 on 27 degrees of freedom
Multiple R-squared: 0.163, Adjusted R-squared: 0.101
F-statistic: 2.629 on 2 and 27 DF, p-value: 0.09054とでます
Run = -0.02119*Hight - 0.02375*Weight + 15.57234
相関係数の2乗であるR2が0.1であんまり相関自体は強くないですし、身長と体重は走行距離に同じ方向性に作用するみたいですね。
各指標の相関係数を計算させたグラフを書かせると
y <- cor(x1)
pheatmap(y)
といった具合で、身長と体重はよく相関するんですが、走行距離との相関はあまりありません。
これは体重と走行距離の関係を見てもよくわかると思います

結論としてはサッカー選手は体格が良いと走れないというわけではないようですね。また体重が75kgまでは体重と走行距離は逆相関、それ以上は体重と相関するようですが、このあたりの意味合いはわかりません。
念のためpositionとも相関をとってみたのですが、

どうも違うようですね。これについてはもう少し分析が必要なようです。
同様のことをpythonでも少しやってみたのですが、
環境設定して、データを読み込んで
%matplotlib inline
from sklearn.cluster import AffinityPropagation, KMeans, DBSCAN, SpectralClustering
from sklearn.manifold import MDS, TSNE, Isomap
from sklearn.metrics import silhouette_score
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy.linalg import logm, expmdf_wine = pd.read_csv('football2.txt', sep="\t",header=0, index_col=None)
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
ln = linear_model.LinearRegression()線形回帰の環境設定をしてから、Runのデータだけ説明変数に使わないので落とします
X =df_wine.drop("Run",1)
Y = df_wine.Run
線形回帰して、回帰係数をもとめると
coef = ln.coef_
names.shape
coe = pd.DataFrame(coef.reshape(1,3), index=["coef"], columns=names)
coe
といった形で求められます
これだけだと面白くないので、もとのデータからpositionを除いてデータをつくり、Normalizeして
df_wine_2 = df_wine.T
print(df_wine_2)
df_wine_2 = pd.DataFrame(df_wine_2)
X = df_wine.iloc[:, :-1].values
X = (X - X.mean(axis=0)) / X.std(axis=0)
MDSプロットで可視化してみると
mds = MDS()
mds_coords = mds.fit_transform(X)
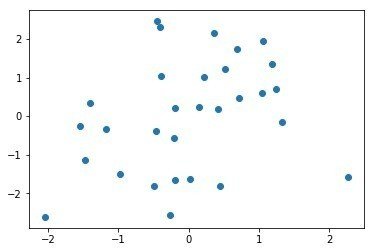
plt.scatter(mds_coords[:,0], mds_coords[:,1])なんか二つのクラスターに分かれるんですよね。。
いまひとつこのプロットのカラー表示がうまくいっていないので恐縮なのですが、ポジションで色分けしてやると(3つ目のポジションFWがでていない。どなたかご存知ならうまく色付けする方法を教えてください)、なんとなくうまくわかれるので、身長と体重と走行距離の情報を入れると、DFかMFかは区別つけられるということでしょうか??
pre_cluster_lables = np.array([0,0,0,0,1,1,1,1,1,2,0,0,0,0,1,1,1,1,1,2,0,0,0,0,1,1,1,2,2,2])
cmap = plt.cm.get_cmap('gnuplot2', len(pre_cluster_lables))
plt.scatter(mds_coords[:,0], mds_coords[:,1], c=pre_cluster_lables, cmap=cmap)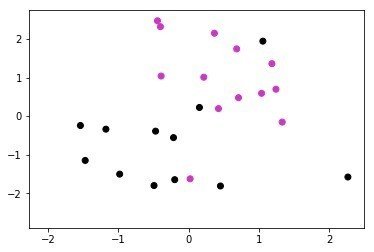
とまあサッカーネタで分析してみました。
