2-4. 2分探索法の最大比較回数

2025年2月13日 14:43

　本記事では、2分探索法の最大比較回数を求めるアルゴリズムについて解説します。問題のレベルは、基本情報技術者試験レベルです。

問題　ある電話番号をあらかじめ整列された1,000人の電話番号から２分探索法を用いて探索するとき、最大何回の比較で見つかるか。ただし、一致する番号が見つからないこともあるものとする。

ア　7
イ　8
ウ　9
エ　10

解説

　2分探索法では、探索のたびに探索範囲が半分になっていきます。実際には、1～1,000 の範囲では中央の値は501番目ですから、その値より小さければ500古文、大きければ499個というように探索範囲は少し違いますが、単純に半分ずつに減っていくと考えます（半分が小数になるときは切り上げ）。
　したがって、最初の探索で一致しなければ探索範囲の半分の500となります。次は250、そして、125、63、32、16、8、4、2、1 というように探索範囲が絞られていきます。そして、通常は探索範囲が2となった時点で見つかると考えられています。しかし、最悪の場合には、それでも見つからず、最後に探索範囲が1となったときにやっと見つかることもあるので、最大比較回数は、探索範囲が1となった時点と考えます。
　探索範囲が2になるまでには8回の探索が行われ、そして、探索範囲の中央値と比較します。平均比較回数として考えられているのはこの時点ですから、9回です。そして、最大比較回数、つまり、最悪の場合は、もう一回比較が行われるので、10回ということになります。
　逐次探索法では、平均比較回数が500回です。2分探索法では、平均比較回数が9回ですから、圧倒的に性能が良いことが分かります。そして、その差はデータ数が多くなればなるほど開いていきます。
　ただし、2分探索法を使うためには、前提として整列されているという条件があります。じつは、この整列の計算量は逐次探索よりも大きいので、1回だけでの探索の場合、逐次探索の方が効率的です。しかし、繰返し探索を行うのであれば、2分探索法の方が効率的になっていきます。

補足1

1. 探索範囲が2になるまでの回数

　2分探索法では、データの個数を n とすると、1回の探索ごとに探索範囲が約半分に減少します。そのため、探索範囲が2になるまでの回数を考えると、次のようになります。

ステップ1: 初期の探索範囲は1,000（1～1,000のデータがある）
ステップ2: 1回目の比較 → 約500（中央の値を比較し、探索範囲を半分にする）
ステップ3: 2回目の比較 → 約250
ステップ4: 3回目の比較 → 約125
ステップ5: 4回目の比較 → 約63
ステップ6: 5回目の比較 → 約32
ステップ7: 6回目の比較 → 約16
ステップ8: 7回目の比較 → 約8
ステップ9: 8回目の比較 → 約4
ステップ10: 9回目の比較 → 約2（この時点で探索範囲が2になった）

このように、探索範囲が 2 になるまで 9回の比較 が行われます。

2. 中央値と比較する

探索範囲が2になった時点では、残っている2つの候補のうち、中央値（つまり、最初の要素）と比較を行います。
この比較によって、求める値が中央値と一致する場合はこの時点で見つかります。
しかし、一致しなかった場合は、最後の1つだけが残ります。

3. 最大比較回数（最悪ケース）

中央値と比較しても 見つからなかった場合、最後に残った1つの要素と比較することになります。
この追加の1回の比較によって 10回目の比較 が行われます。

つまり、

中央値の時点で見つかる場合 → 9回の比較
中央値で見つからず、最後の1つをチェックする場合 → 10回の比較（最悪ケース）

4. まとめ

探索範囲が2になるまでに8回の比較が必要
9回目の比較で中央値と照合
最悪の場合、さらに1回の比較が必要
よって、最大比較回数は10回となる

　このように、2分探索法では 最大でも10回の比較で必ず結果が得られる ため、1,000件のデータに対しても非常に効率的に検索できることが分かります。

補足2

Java と Python でコーディング

Javaでの実装（2分探索法）

public class BinarySearch {
    public static int binarySearch(int[] arr, int target) {
        int left = 0;
        int right = arr.length - 1;
        int comparisons = 0;

        while (left <= right) {
            comparisons++;
            int mid = left + (right - left) / 2;

            if (arr[mid] == target) {
                System.out.println("Found in " + comparisons + " comparisons.");
                return mid;
            } else if (arr[mid] < target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }

        System.out.println("Not found. Total comparisons: " + comparisons);
        return -1;
    }

    public static void main(String[] args) {
        int[] numbers = new int[1000];
        for (int i = 0; i < 1000; i++) {
            numbers[i] = i + 1;
        }

        int target = 999; // 探索対象の番号
        binarySearch(numbers, target);
    }
}

Pythonでの実装（2分探索法）

def binary_search(arr, target):
    left, right = 0, len(arr) - 1
    comparisons = 0

    while left <= right:
        comparisons += 1
        mid = left + (right - left) // 2

        if arr[mid] == target:
            print(f"Found in {comparisons} comparisons.")
            return mid
        elif arr[mid] < target:
            left = mid + 1
        else:
            right = mid - 1

    print(f"Not found. Total comparisons: {comparisons}")
    return -1

# 配列の準備（1～1000の連番）
numbers = list(range(1, 1001))

# 探索対象
target = 999
binary_search(numbers, target)

実行結果（例えば 999 を探した場合）

Java と Python のどちらのコードでも、出力は次のようになります。

Found in 10 comparisons.

また、存在しない値（例えば 1001）を探した場合：

Not found. Total comparisons: 10

最大で 10回 の比較で探索が完了することが確認できます。

補足3

2分探索法では、最大比較回数（最悪ケース）は 「探索対象の個数 nn に対する対数値」 で表されます。

最大比較回数の公式

log2(n)+1

（※log2(n) は n を超えない最大の2の累乗の指数 を取る）

具体例

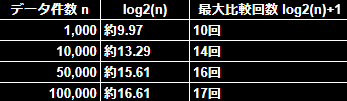
**図1. 最大比較回数（最悪ケース）は「探索対象の個数 𝑛 n に対する対数値」で表される**

考察

データ数が 10倍 になっても、比較回数は 約3～4回しか増えない。
これは 対数関数の性質 によるもので、データが 爆発的に増えても検索コストはあまり増えない 。
例えば、1,000,000件（100万件） でも 最大20回の比較 で済む。

まとめ

1,000件 → 最大10回
10,000件 → 最大14回
50,000件 → 最大16回
100,000件 → 最大17回
1,000,000件（100万件） → 最大20回

　このように、データ件数が増えても比較回数は対数的にしか増えないため、2分探索は非常に効率的 です。

補足3　
整列処理（ソート）の速度と負荷について

　2分探索は高速ですが、「整列済みのデータが前提」 なので、データの整列（ソート）が必要になります。
　ソートにはどのくらいの処理時間や計算コストがかかるのかを見てみましょう。

1. ソートの計算量

　ソートアルゴリズムには様々な種類がありますが、一般的に使われるものは O(nlogn)の計算量を持ちます。
例えば、

クイックソート（平均）
マージソート
ヒープソート

は、すべて O(nlogn)で動作します。

しかし、最悪ケースを考えると…

クイックソートの最悪ケース → O(n^2)（※要素が既に整列済みの場合など）
ヒープソート・マージソート → 最悪でも O(nlog⁡n)

2. データ件数ごとのソートと2分探索の比較

🔹 ポイント

2分探索の比較回数は 対数的に増える ため ほぼ影響なし。
ソートは O(nlog⁡n)なので、データが大きくなると処理負荷が増加する。

3. 実用的な影響

1回だけ探索する場合
→ 逐次探索（線形探索, O(n)）のほうが速い。
→ なぜなら、ソートが必要な分、2分探索のほうがコストが大きい ため。
複数回の探索を行う場合
→ 一度ソートしておけば、2分探索が圧倒的に速い。
→ 例えば、大量の検索をするデータベースや検索エンジンでは 整列済みのデータに対して2分探索が有効。

4. どんな場面で有効か？

5. 結論

ソートには O(nlog⁡n)のコストがかかるため、1回の検索なら逐次探索の方が効率的。
2分探索はデータ量が増えても検索回数が増えにくい（対数的にしか増えない）ため、大量の検索には適している。
そのため、検索を何度も行う場合は「先にソートして2分探索」の方が結果的に高速になる。

　例えば、検索を 1回だけ 行うなら逐次探索（線形探索）の方が速いですが、100回・1000回と検索するなら、最初にソートして2分探索を使った方が総合的に速い ということです。

以上です。