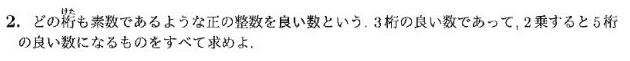Pythonで数オリ予選を合格してみた
はじめに
タイトルの通り、半分おふざけの遊び的な内容となっています。
元ネタはこちらになります↓↓
趣旨
プログラミングの力を借りて数学オリンピックの問題を楽に倒していくという爽快感を味わう企画です。
日本数学オリンピック(JMO)2019年の予選について、楽に合格点をとりたいと思います。この年は全12問中5問正解で合格です。
問題の出典(数学オリンピック財団)はこちら↓↓
ルール
合格していく前に多少のルールを設定しておきます。無差別級も悪くないですが、制限があった方が面白いと思いルールを設定しました。
① できるだけ計算で殴り倒す(⇔できるだけ数学的な考察をしない)
② 計算量が膨大なときは絞る(⇔少しだけ数学的に考察。競プロ的?)
③ Pythonでインポート可のモジュールはデフォルト+Numpyのみ。
ではいってみましょう!
JMO 予選 2019 問1
x,y,z が 1以上30以下であるのは自明ですが、全組合せを考えても高々 2.7万通り(30×30×30通り)しかありません。全チェックで倒せます。
# jmo2019-1.py
for x in xrange(1,31):
for y in xrange(1,31):
for z in xrange(1,31):
if (x+x*y+x*y*z) == 31 and (x<y<z):
print x,y,z
実行結果。
1 2 14
1 3 9
execution time: 0.008s答えはあっていました。次に行きます。
JMO 予選 2019 問2
各桁はそれぞれ素数 2, 3, 5, 7 のいずれかなので 4通りです。つまり、題意の 3桁の数は高々 64通り(4×4×4通り)しかありません。全チェックで倒せます。
【実装】良い数のチェック(is_goodnum関数)を正規表現を用いた文字列のマッチングとして実現していますが、どのような方法でもOKです。
#jmo2019-2.py
import re
primes = [2,3,5,7]
for d1 in primes:
for d2 in primes:
for d3 in primes:
n = d3*100 + d2*10 + d1
N = n**2
if is_goodnum(N) and (10**4<=N<10**5):
print n
def is_goodnum(n):
if re.match( '[2357]{5}', str(n) ):
return True
else:
return False
実行結果。
235
execution time: 0.001s答えはあっていました。これも楽勝ですね。
JMO 予選 2019 問3
9個の整数を並べて条件に合うものをカウントしたいと思います。9!≒ 36.3万通りなので計算時間は少しかかりますが、全チェックで倒せる範囲でしょう。
【実装】① 9!通りの順列を全パターンを作り(itertools.permulations関数を使用)、② 順列を 3×3の表に格納して(ndarrayオブジェクトとreshapeメソッドを使用)、③ 条件チェックを行列計算で行う(check_condition関数)。
#jmo2019-3.py
import numpy as np
import itertools
nums = range(1,9+1)
count = 0
for p in itertools.permutations(nums):
tbl = np.array(list(p)).reshape(3,3)
if check_condition(tbl):
count += 1
print count
def check_condition(tbl):
# horizontal check
diff_h = tbl[:,0:2] - tbl[:,1:]
diff_h = np.abs(diff_h)
if not np.all( diff_h <= 3 ):
return False
# vertical check
diff_v = tbl[0:2,:] - tbl[1:,:]
diff_v = np.abs(diff_v)
if not np.all( diff_v <= 3 ):
return False
return True
実行結果。
32
execution time: 13.078s答えはあっていましたが、計算時間が前の2問よりもかなり長くなっています。今回は解ければOKなので良しとします。
JMO 予選 2019 問5
余りの条件を満たす整数は無数に存在すると思われるので、残念ながら範囲の絞り込み(=計算量を見積もること)ができません。
現実的な時間内に答えが求まるか分かりませんが、小さい数から順に条件を満たす整数をチェックしていくしかありません。+1ずつして整数をチェックすると日が暮れる可能性があるので、数学的な考察を入れて高速化します。
【考察】条件より整数 n は 103 i + 34,100 j + 33,97 k + 32 のいずれの方法でも表せる。① 刻み幅の大きい 103 i + 34 で表して i をインクリメントすれば103倍高速。② n = 100 j + 33 より n は奇数だから n = 103 i + 34 が奇数であるためには、i が奇数である必要がある。i を奇数としてインクリメントすることで刻み幅が大きくなりさらに2倍高速。
【実装】① 余りの条件を1つ利用して候補の数を算出( n = 103*(2*i+1)+34 とする)、② 残りの 余りの条件2つに適合するか順にチェックする(厳しい条件である n % 100 == 33 を先にチェックして無駄な演算を行わない)
# jmo2019-5.py
i = 0
while True:
n = 103 * (2*i+1) + 34
if (n % 100) != 33:
i += 1
continue
if (n % 97) != 32:
i += 1
continue
break
print n
実行結果。
333033
execution time: 0.081s無事、答えが出てきました。あっていました。デカい数が答えじゃなかったので、結果的に早く計算が終わったといったところですね。問題に助けられました。高速化しないと計算時間が16秒以上かかるようです。
JMO 予選 2019 問9
各マス 4通りで 16マスあるので、全チェックだと 4 の 16乗 ≒ 43億通りあるということですね。全チェックはあまり現実的ではなくすごく時間がかかってしまうので、計算量を減らす工夫を行います。
【考察】4マスのうち3マスが決まると残りの 1マスが定まることを利用します。上3行だけ全パターンを考えてあげて、残りのマスを計算で一意に定めることでチェックします。各行は64通り(4×4×4×1通り)あります。よって全部で、64 の 3乗 ≒ 26.2万通りなのでチェックしきれます。
【実装】コードが少し長くなってしまいましたが、やっていることはシンプルです。要点を以下に図解しました。
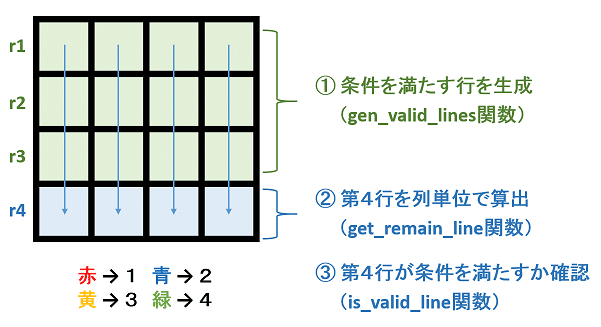
# jmo2019-9.py
import itertools
rows = gen_valid_lines()
count = 0
for r1 in rows:
for r2 in rows:
for r3 in rows:
r4 = get_remain_line(r1,r2,r3)
if is_valid_line(r4):
count += 1
print count
def is_valid_line(line):
n = get_remain_num(line[0],line[1],line[2])
if n == line[3]:
return True
else:
return False
def get_remain_line(l1,l2,l3):
l4 = [0,0,0,0]
for i in xrange(4):
l4[i] = get_remain_num(l1[i],l2[i],l3[i])
return l4
def get_remain_num(n1,n2,n3):
if n1 == n2:
if n2 == n3:
# condition (1)
return n1
else:
# condition (2)
return n3
else:
if n2 == n3:
# condition (2)
return n1
else:
if n1 == n3:
# condition (2)
return n2
else:
# condition (3)
n = (1+2+3+4) - (n1+n2+n3)
return n
def gen_valid_lines():
nums = range(1,4+1)
lines = []
# condition (1)
for i in nums:
new = [i,i,i,i]
lines.append(new)
# condition (2)
for p in itertools.combinations(nums,2):
a = p[0]
b = p[1]
lines.append( [a,a,b,b] )
lines.append( [a,b,a,b] )
lines.append( [a,b,b,a] )
lines.append( [b,a,a,b] )
lines.append( [b,a,b,a] )
lines.append( [b,b,a,a] )
# condition (3)
for p in itertools.permutations(nums):
new = list(p)
lines.append(new)
return実行結果。
262144
execution time: 1.372s答えがあいました。どうやらチェックにかけた全てのパターンが条件を満たしたようです。
さいごに
合格点ボーダーをとることができました。無事合格ですね。
ただお分かりの通り、幾何などプログラムだけで解くには難しい問題をスルーしていますので、他の年だと合格は結構きびしいです。
お遊びではありますが、数学の問題を違った視点で見れて面白かったです。
数学的な解法についてはこちらで真面目に説明しております↓↓