
Time Decayと本質的価値
前々回の記事で、1ヶ月先の日経平均先物が28500円よりも上にあればプットオプションの売りは8,000円の利益になりますねって話があったと思います。あれ、実際どうですか?
例え1ヶ月先とは言え、最近かなり上がったし調整もありそうだから7000円下がることもなくはないんじゃないか?と思う人もいると思います。それはそうですよね。つい最近なんて、下がる下がると言われ続けていたのにあれよあれよと3,000円も上昇したのだから、7,000円下がる可能性だって十分ありますよね。
では、明日はどうですか?次の日、7,000円下がると思いますか?これはどうでしょう。多少なりとも先物経験者なら「さすがに明日1日で7,000円も動かないw」と、なると思います。
はい、これが今回お話するTime Decayと本質的価値です。
Time Decay(時間的価値)
これは時間を価値に置き換えるというものです。
一旦、コールオプションの買い手側の立場になって考えてみましょう。権利行使価格35000円のコールオプションを500円で買いました。現在の先物価格は34000円だったとしましょう。
損益分岐点は、35500円になるので、まだ1501円以上も上昇しなければなりません。ところが満期日までの日数が20営業日あったらどうでしょうか?20営業日あれば、1501円上昇する可能性は感じられますよね。でも、満期日までの日数が1~3営業日だったら希望は薄いです。

満期までの時間が多ければ多い程、将来どうなるか分からない可能性に価値が発生します。ただ時間が経てば経つほどみるみる価値は減少していき、最後は急速に価値が無くなります。これを時間的価値の減少と呼びます。
本質的価値
次に求めるのは、そのオプションそのものにおける現時点における価値です。このことを本質的価値と呼びます。
現在の日経平均先物価格:34000円
コールオプション:35000円
プレミアム:500円
先ほどと同じ条件で見ていきましょう。時間的価値という概念は一旦忘れると、現時点におけるこのコールオプションの価値は全く無いですよね。だって、普通に34000円で売られている先物をわざわざ1000円高い35000円で買う人はいないので、35000円で買える権利は無価値となります。
では、こちらはどうでしょうか?
現在の日経平均先物価格:35000円
コールオプション:34000円
プレミアム:500円
逆のパターンですね。これは価値がありますよね。34000円で先物を買う権利を有していることになるので、プレミアムで500円を支払っていたとしても、差額の500円が利益です。
では、こちらはどうでしょう。
現在の日経平均先物価格:34500円
コールオプション:34000円
プレミアム:500円
これも無価値ですね。34000円で買える権利を持っていて、日経平均先物価格は34500円だけど、コールオプションを買う為に500円を支払っているので、500円の利益と500円の損失の相殺で、±0円。無価値ですね。
これらをそれぞれこう呼びます。
Out of The Money(アウト・オブ・ザ・マネー)
In The Money(イン・ザ・マネー)
At The Money(アット・ザ・マネー)
Out of The Money
アウト・オブ・ザ・マネーは、略してOTMと書きます。こちらはそのオプションが現在、全くの無価値状態であることを意味しています。
In The Money
イン・ザ・マネーは、略してITMと書きます。こちらはOTMとは逆に、現時点で価値を有している状態であることを意味しています。
At The Money
アット・ザ・マネーは、略してATMと書きます。こちらはOTMと同様に無価値状態ではありますが、±0円状態なので、中間地点を意味しています。
当然、現時点における価値が高ければ高い程、プレミアム(オプションを取引する値段)は高くなるので、ITMになればなるほど価値は高くなり、OTMに近づけば近づく程、プレミアムも安くなっていきます。
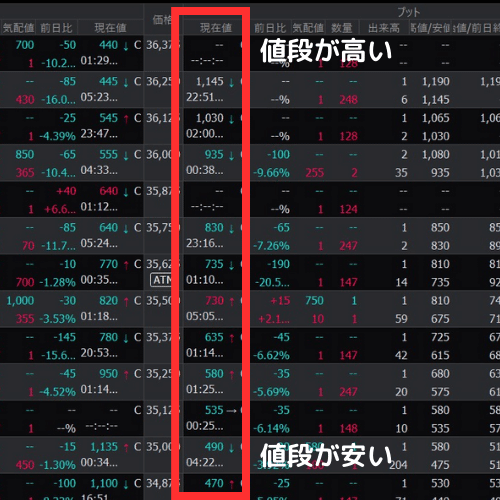
現在のプットオプションの価格ですが、ATMの値段は735円になっています。一方、36250円の値段は1145円と高額です。また、35000円のプットは490円と安いですね。
ITMに近づけば近づく程そのオプションのプレミアム(値段)は高騰し、OTMに近づけば近づく程、プレミアムは安価になる。
これが本質的価値です。
プレミアムの計算式
オプションの価値(プレミアム)は、今回ご説明したTime Decayと本質的価値の2つを足して計算されます。
プレミアム = Time Decay + 本質的価値
オプショントレーダーは、オプションを売買する時はもちろん、戦略を練る時にはこのTime Decayと本質的価値の両側面から将来を予測していかなければなりません。
今回ご説明したTime Decayと本質的価値は、将来の先物価格を予想(考察)する上で重要な要素になってくるので、しっかりと理解し、覚えて下さい。
