令和6年度　特別区教養試験　判断推理解説

No１０　総当たり戦　引き分け

問題

A~Fの6チームが、サッカーの試合を総当たり戦で2回行った。今、2回の総当たり戦の結果について、次のア～エことが分かっているとき、確実にいえるのはどれか。

ア：各チームの引き分け数は、Aが5試合、Bが2試合、Cが3試合、Dが6試　　　　　　合、Eが2試合、Fが4試合であった。
イ：各チームとも2チーム以上と引き分けた。
ウ：AはBと引き分けなかった。
エ：Dはすべてのチームと引き分けた。

１：Aは、C、D、Eと1試合ずつ引き分けた。
２：Bは、Cと少なくとも1試合引き分けた。
３：Cは、Fと少なくとも1試合引き分けた。
４：Dは、Fと2試合とも引き分けた。
５：FはAと少なくとも１試合引き分けた。

解説

この手の問題は、一つパターンを完成させて、選択肢を消していくと早いです。

Dについて、6回引き分けているので、表にまとめると、

ここで、A~Fの残りの引き分け数は、
A：４　△△△△
B：１　△
C：２　△△
D：１　△
E：１　△
F：３　△△△

この残りの引き分け数から、考えられるパターンを1つ考えます。

Aの2試合とCの2試合がともに引き分けとすると、残りは、
A：△△△△
B：△
C：△△
D：△
E：△
F：△△△
となります。

同様に、
Aの残り2試合とFの2試合
Fの残り1試合とEの1試合
Bの1試合とDの1試合
が引き分けたとしましょう。
表にすると以下の通りです。

この時点で、
１、２、３、４の選択肢が誤りとなるため、消去法で５が正解となります。

偶然試した1つ目のパターンで4つの選択肢が消えましたが、ほかのパターンから試しても、全部のパターンを書きだすよりは消去法が早いです。

No１１　暗号

問題

ある暗号で、「緑色」が「Ⅳえ・Ⅲい・Ⅰお・Ⅰお・Ⅱう」、「赤色」が「Ⅲい・Ⅰお、Ⅱお」と表されるとき、同じ法則で「黒色」を表したのはどれか。

１：「Ⅱえ・Ⅳあ・Ⅰう・Ⅲい・Ⅰあ」
２：「Ⅲあ・Ⅲえ・Ⅱえ・Ⅰい・Ⅰお」
３：「Ⅳお・Ⅲい・Ⅰう・Ⅲあ・Ⅱう」
４：「Ⅳお・Ⅳう・Ⅴあ・Ⅰお」
５：「Ⅳお・Ⅳう・Ⅴお・Ⅲお・Ⅴう」

解説

暗号の問題は例を当てはめるところから始めましょう。

「緑色」が5個の暗号、「赤色」が3個の暗号で構成されていますが、ひらがなだと「あかいろ」を表すのに４個の暗号が必要となります。よってひらがなではありません。

次に英語に変換してみると、「緑色」→「green」、「赤色」→「red」となり、暗号の個数と一致します。次はこれを当てはめてみましょう。

g：Ⅳえ
r：Ⅲい
e：Ⅰお
e：Ⅰお
n：Ⅱう

r：Ⅲい
e：Ⅰお
d：Ⅱお

となります。ここで、暗号の法則を考察してみましょう。
隣り合っているdとeについて、
d：Ⅱお、e：Ⅰお、であることから次のように推測されます。

a：Ⅴお
b：Ⅳお
c：Ⅲお
d：Ⅱお
e：Ⅰお

数字部分が5個さかのぼっていることから、数字が5個さかのぼるとひらがな部分が1個さかのぼっていると推測すると、

a~e：お　Ⅴ～Ⅰ
f~j：え　Ⅴ～Ⅰ
K~o：う　Ⅴ～Ⅰ
p~t：い　Ⅴ～Ⅰ
u~y：あ　Ⅴ～Ⅰ
z：？

となります。
この法則に当てはめると、「黒色」つまり「black」は、

b：Ⅳお
l：Ⅳう
a：Ⅴお
c：Ⅲお
k：Ⅴう

となり、５が正解となります。

No１２　焼肉と寿司

問題

寿司屋か焼肉屋のどちらかに行きたいA~Eの5人がいる。今、意見の調整を次のア～ウの順に実施し、最終的に5人全員がすし屋に行く意見でまとまったとき、確実に言えるのはどれか。ただし、それぞれの意見の調整では、3回とも3人の中の意見の一致する2人の説得により、他の1人が意見を変えたものとする。

ア：1回目は、A、B、Cで実施した。
イ：2回目は、A、C、Dで実施した。
ウ：3回目は、B、D、Eで実施した。

１：調整前は、寿司屋に行きたいものが２人、焼き肉屋に行きたい者が3人であった。
２：調整前は、Bは焼き肉屋に行きたい意見を持っていた。
３：調整前は、Cは焼き肉屋に行きたい意見を持っていた。
４：調査の結果、Dは自分の意見を2回変えた。
５：Eの調整前の意見は、寿司屋であったか焼き肉屋であったかはわからない。

解説

これもNo10と同様にパターンと消去法でやっていきましょう。
最終的に寿司で一致するので表にまとめると下のようになります。

Eだけは1度しか話し合いに参加していないので、Eが最初焼肉だったと仮定すると、

3回目の結果は
B：す→す
D：す→す
E：や→す

ここで1回目と２回目でさらにパターンの分岐があるのですが、１、3回目に参加したBについて、Bが最初焼肉であったと仮定すると、

1回目の結果は
A：す→す
B：や→す
C：す→す

2回目の結果は
A：す→す
C：す→す
D：や→す

となり、表にまとめると以下の通りです。

この時点で、選択肢の３、４を消去することができます。

次に、残る選択肢１、２、５のうち、２を消去するため、Bが最初寿司であった場合を考えます。
これが成立すれば、2を消去することができます。

Bが最初寿司であった場合、Bは1回目、3回目ともに＜す→す＞となります。
この場合1回目のパターンとして

①
A：す→す
B：す→す
C：や→す

②
A：や→す
B：す→す
C：す→す

の2パターンが考えられますが、①のパターンを試してみましょう。
この場合、2回目は

A：す→す
C：す→す
D：や→す

3回目は

B：す→す
D：す→す
E：や→す

となり、Bが最初に寿司でも成立するため、２を消去することができます。
表にすると、以下の通りです。

この2つのパターンを試してみて、時間が無ければ、Eはどちらも最初は焼肉であり、寿司と焼肉の最初の人数はどちらもそれぞれ2人、3人であることから目星をつけて5を消去し1を選んで構わないと思います。

この先も同様にほかのいくつかのパターンを試すと5を消去することができます。

よって1が正解となります。

No１３　3人の選挙

この問題には、不備があるため、厳密には正解がありませんが、一般的な解法を解説していきます。

問題

ある学校の生徒会役員の選挙が行われた。A、B、Cの３人の候補者のうち、生徒会役員を生徒全員の投票によって決定する。今、次のア～エのことが分かっているとき、確実に言えるのはどれか。

ア：生徒は、最大2人まで選んで投票することができた。
イ：生徒は、少なくとも1人に投票した。
ウ：A又はBに投票した生徒はCには投票しなかった。
エ：Bに投票しなかった生徒はCに投票した。

１：Aに投票しなかった生徒は、Bに投票した。
２：Aに投票しなかった生徒は、Cに投票した。
３：A及びBに投票した生徒はいなかった。
４：Aのみに投票した生徒がいた。
５：Bのみに投票した生徒がいた。

解説

この問題は、すべての投票パターンを書き出し、条件に矛盾するパターンを消去した後、選択肢と照らし合わせましょう。

まず、A、B、Cのうち、投票した者を大文字、投票しなかったもの小文字で表すと、

ABC、ABc、AbC、Abc、aBC、aBc、abC、abc

の8パターンが考えられます。表にまとめると以下の通りです。

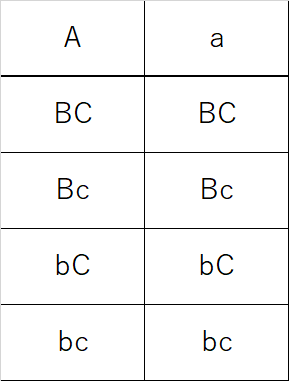
条件と比較していくと、

アより、3人に投票した生徒はいないため、ABCは消去します。
イより、だれにも投票していない生徒はいないため、abcは消去します。
ウより、AとCの両方またはBとCの両方に投票した生徒はいないため、AbC、aBCは消去します。
エより、Bに投票せず、Cにも投票しなかった生徒はいないため、Abcは消去します。

表にすると、以下の通りです。（黄色のパターンが消去されます）

残りのパターンは、
ABc、aBc、abC
となるため、これらパターンを使って選択肢を検討していきます。

選択肢３、４は誤りです。
選択肢５は正解です。
しかし、選択肢１、２は確実とはいえないものの、可能性としては残るため、問題として不備があると思われます。

問題１４　カードゲーム

問題

１～７の互いに異なる数字が１つ書かれた７枚のカードがある２組ある。A、Bの２人がこの組を１つずつ手札として以て、各自が手札からカードを１枚ずつ出し合い、出したカードの数字を比較して、数字の大きいカードを出したほうを勝ち、同じ場合は引き分けとするゲームを行う。今、このゲームを手札がなくなるまで行い、次のア～エのことが分かっているとき、確実にいえるのはどれか。ただし、一度出したカードは手札に戻さないものとする。

ア：Aが２回目に出したカードの数字は６であり、Bが最後に出したカードの数字は１であった。
イ：Aが奇数回目に出したカードの数字はすべて奇数であった。
ウ：Aは３回、Bは４回勝って、引き分けはなかった。
エ：Bが勝ったときのカードの数字の差はすべて１であった。

解説

この問題は表に整理して考えましょう。
アの条件を表にまとめると以下の通りです。

イの条件について、奇数回目と偶数回目の条件をまとめやすくするため、表を少し変えてみましょう。
また、Aは奇数回目に奇数のカードを出しているため、偶数回目には２か４のカードを出していることが分かります。表にまとめると以下の通りです。

ウより、引き分けがないことから、Aの７回目に１は入りません。
エより、Aが１を出したとき、Bは１点差で勝っていることから２を出したことが分かります。
また、Aが２を出したとき、Bが１を出すことはないため、Bは３を出して勝っています。

ウより、Bは４勝しており、勝ったときの点差は１であったことから、BはAが偶数を出した３回と、奇数を出したうちの１回に勝利していることが推測されます。

この時点で、Aの残りのカードは３と５と７、Bの残りのカードは４と６であるため、考えられるパターンは以下の１つのみです。

よって、正解は２となります。

No１５　１０個の駅と所要時間

問題

次の図のような１０この駅からなり、両方向に電車を運行させている環状線がある。各駅とも、両隣の駅までの所要時間が２分又は３分であり、A駅から各駅までの所要時間を表のとおりとするとき、所要時間が最も短い経路として妥当なのはどれか。ただし、表の所要時間はより短い経路での時間を示したものであり、同一区間であれば、所要時間は両方向とも同じであるものとする。

１：B駅からI駅まで
２：D駅からE駅まで
３：D駅からJ駅まで
４：E駅からI駅まで
５：I駅からJ駅まで

解説

隣の駅までの所要時間が２分か３分なので、ここから推測していきます。

まず、Aの隣の駅はAからの所要時間が３分以下なのでCとGになります。
CとGの隣の駅はAから５分以内なのでEとIになります。

ここまでをまとめると以下の通りです。（CとG、IとEは順不同です）

Iの隣の駅はAから７分以内なのでD、Eの隣の駅はAから８分以内なのでJとなります。
さらに、Dの隣の駅はAから１０分以内なのでF、Jの隣の駅はAから１１分以内なのでBとなります。
残りのHについては、Aからの最短時間が１２分であるため、FからHの所要時間が２分であり、BH間の所要時間は不明（２分または３分）です。

ここまで出来たら選択肢を検討していきましょう。最短時間を比較するため、BH間は仮に２分かかるとします。
（経由駅はこの図の通りの配置の場合です。）

１：BI間→H経由で１０分、J経由で１５分→最短で１０分
２：DE間→I経由で１２分、F経由で１３分→最短で１２分
３：DJ間→I経由で１５分、F経由で１０分→最短で１０分
４：EI間→J経由で１６分、G経由で９分→最短で９分
５：IJ間→C経由で１２分、D経由で１３分→最短で１２分

よって４が正解となります。