【測量士補資格試験】座標からの求積

測量士の八重樫です。こんにちは。

測量士補の資格試験で出題される点数の取りやすい問題について
【測量士補資格試験】簡単な計算問題で点を稼ぐ
で、解説をした。
ここでは、上記のnoteに含まなかった問題のうち、座標からの求積について解説する。

簡単な計算問題でより多くの点数が取りたいという方は、上記リンクのnoteを買っていただけると有り難い。

座標からの求積

このような問題がある。

点Ａ，Ｂ，Ｃ，Ｄで囲まれた土地に杭を設置することとなった。各点の座標値は表 27 のとおりである。
点Ｃの座標を X＝26.50 m，Y＝26.40 m と誤って杭を設置した場合，杭に囲まれた面積は正しい値に比べてどれだけの較差を生じるか。
最も近いものを次の中から選べ。
なお，関数の値が必要な場合は，巻末の関数表を使用すること。

　　点　　X座標 ( m )　　Y座標 ( m )
　　A　　　+ 40.00　　　 + 40.00
　　B　　　+ 35.50　　　 + 30.20
　　C　　　+ 26.40　　　 + 26.50
　　D　　　+ 17.90　　　 + 38.20

　　1.　 0.41 m2
　　2.　 0.48 m2
　　3.　 0.82 m2
　　4.　 0.96 m2
　　5.　 1.92 m2
（ 平成30年 測量士補試験問題集 No.27 ）

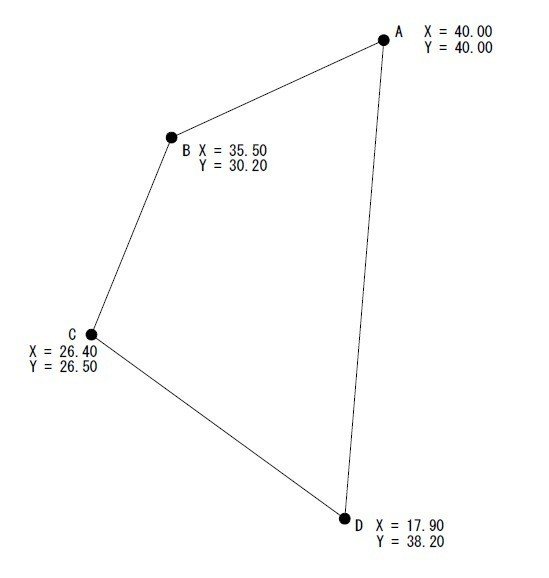
面積の差を求める問題だ。
面積には様々な求め方がある。

●座標法による求積
●倍横距法による求積
●ヘロンの公式による求積
●三斜法による求積

このnoteでは、座標法による求積の解き方について解説する。

座標法による求積

実務の経験がない人にとっては馴染みがないかもしれない。
実務の経験がある人にとっては、必ず一度は見たことがあるだろう。
現在では、求積の際に最も多く用いられる計算だ。

このような表を作成する。
そして、( Yn + 1 ) - ( Yn - 1 ) を計算し、表に書き加える。
この ( Yn + 1 ) は、点Aで言えば点BのY座標だ。
同様に、( Yn - 1 ) は、点Aで言えば点DのY座標。

 点A　( Yn + 1 ) - ( Yn - 1 )
30.20 - 38.20 = -8.00

同様に、点B以降の ( Yn + 1 ) - ( Yn - 1 ) も計算しよう。

点B　( Yn + 1 ) - ( Yn - 1 )
26.50 - 40.00 = -13.50

点C　( Yn + 1 ) - ( Yn - 1 )
38.20 - 30.20 = 8.00

点D　( Yn + 1 ) - ( Yn - 1 )
40.00 - 38.20 = 13.50

次に、Xn ✕ { ( Yn + 1 ) - ( Yn - 1) } を計算し、表に書き加える。

点A　Xn ✕ { ( Yn + 1 ) - ( Yn - 1) }
40.00 ✕ -8.00 = -320.00

点B　Xn ✕ { ( Yn + 1 ) - ( Yn - 1) }
35.50 ✕ -13.50 = -479.25

点C　Xn ✕ { ( Yn + 1 ) - ( Yn - 1) }
26.40 ✕ 8.00 = 211.20

点D　Xn ✕ { ( Yn + 1 ) - ( Yn - 1) }
17.90 ✕ 13.50 = 241.65

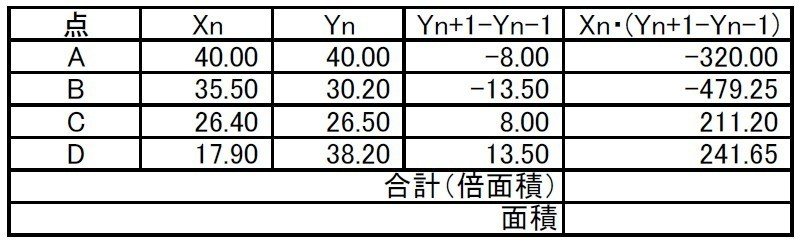
そして、Xn ✕ { ( Yn + 1 ) - ( Yn - 1) } の合計が倍面積になる。

この、倍面積の 1/2 が座標法での求積の解だ。

当然だが、面積なので - になる事はない。
符号を外した数値が面積となる。

どのような計算が行われているかというと

先ず、このような台形の面積を求める。

台形の面積は ( 上底＋下底 ) ✕ 高さ÷２ なので

S1 = ( YA + YD ) * ( XA - XD ) / 2

そして、上図の面積では求めたい４点から成る四角形の外側の面積も含まれている為、除外すべき箇所に台形を作る。

この、外側の台形３つの面積を求める。

S2 = ( YA + YB ) * ( XA - XB ) / 2
S3 = ( YB + YC ) * ( XB - XC ) / 2
S4 = ( YC + YD ) * ( XC - XD ) / 2

最終的に面積を求めたい４点から成る四角形の面積Sは

S = S1 - ( S2 + S3 + S4 )

なので

S =   　( YA + YD ) * ( XA - XD ) / 2
　　- { ( YA + YB ) * ( XA - XB ) / 2 }
　　- { ( YB + YC ) * ( XB - XC ) / 2 }
　　- { ( YC + YD ) * ( XC - XD ) / 2 }

この式のままだと、ややこしいので

　　(　　 YAXA - YAXD　+　YDXA - YDXD
　　　-　 YAXA + YAXB　-　 YBXA + YBXB
　　　-　 YBXB + YBXC　 -　YCXB + YCXC
　　　-　 YCXC + YCXD　-　YDXC + YDXD　) / 2

=　(　　- YAXD + YDXA
　　　　+ YAXB - YBXA
　　　　+ YBXC - YCXB
　　　　+ YCXD - YDXC　) / 2

= { XA * ( YD - YB ) + XB * ( YA - YC ) + XC * ( YB - YD ) + XD * ( YC - YA ) } / 2

これを、冒頭の表にあったような Xn ✕ { ( Yn + 1 ) - ( Yn - 1) } のように表すと

S = Σ [ Xn * { ( Yn-1 ) - ( Yn+1 ) } ] /2

 諸事情により Yn+1 と Yn-1 が入れ替わってしまったが、これは⊿Yを求める為の物なので、計算上の影響はない。

さて、この問題では「点Ｃの座標を X＝26.50 m，Y＝26.40 m と誤って杭を設置した場合の面積の差」を求めなくてはならないので、点Cの座標を X = 26.50m Y = 26.40mとして計算してみよう。

最初に求めた面積との差は

173.20 - 173.68 = -0.48㎡

よって、正解は2だ。

まとめ

ここで解説していない求積法については、類似した問題で角度が与えられている物等があった際には解説しよう。

この問題では
S = Σ [ Xn * { ( Yn+1 ) - ( Yn-1 ) } ] /2
と、少し面倒な公式が出てきてしまった。
これは、土地家屋調査士の試験問題でも使える事があるので、土地家屋調査士を目指す方は覚えておいて損はないかも知れない。

測量士補の資格試験では、このような公式を覚えなくても簡単に解く事が出来る計算問題も多数出題される。
そういった問題については
【測量士補資格試験】簡単な計算問題で点を稼ぐ
で解説しているので、上記のnoteを買っていただけると有り難い。

ありがとうございました。