【測量士資格試験】午前過去問 座標の回転
測量士の八重樫です。こんにちは。
【測量士資格試験】基本的な戦略で書いたように測量士の試験では午前試験で高得点を取る事が重要だ。
そのためには計算問題をきちんとこなす必要がある。
測量士補の試験では出題されなかった計算問題について解説をしていく。
座標の回転
このような問題がある。
次の式は、平面上の点( x , y ) を原点 ( 0 , 0 ) を中心にθ回転させた場合の点 ( X , Y ) の座標を表す式を行列表記したものである。
x = 2.0 , y = -1.0 , θ = 150° とした場合、X , Y の組合せとして最も適当なものはどれか。次の中から選べ。
なお、関数の値が必要な場合は、巻末の関数表を使用すること。
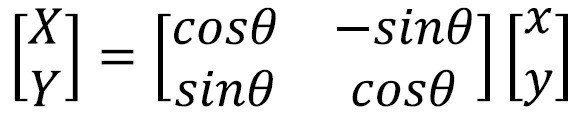
X Y
1. -0.914 1.707
2. -1.232 1.866
3. -2.232 0.134
4. -2.732 0.366
5. 2.232 0.134
( 平成29年 測量士試験問題集 午前 No.5 )

先ずは式を展開する。
X = x*cosθ - y*sinθ
Y = x*sinθ + y*cosθ
次に、問題文の数値を当てはめる。
X = 2 * cos150° - ( -1 ) * sin150°
= 2 * ( -0.86603 ) - ( -1 ) * 0.50000
= -1.73206 - ( -0.50000)
= -1.232
Y = 2*sin150° + ( -1 )*cos150°
= 2 * 0.50000 + ( -1 ) * ( -0.86603 )
= 1 + 0.86603
= 1.866
なので、2が正解だ。
測量士補の計算問題まででは出てこなかったθが90°を超える三角関数が使われている。
これはどういう事かというと
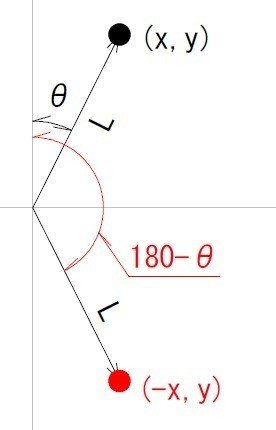
このように、方向角θ、距離L、座標 ( x,y ) の点と、方向角180-θ、距離Lの点を図にすると、180-θの点は座標が ( -x,y )である事がわかる。
そして、距離Lは
方向角θの点では
cosθ = x / L
L = cosθ / x
sinθ = y / L
L = sinθ / y
方向角180-θの点
cos ( 180-θ ) = -x / L
L = cos ( 180-θ ) / -x
sin( 180-θ ) = y / L
L = sin ( 180-θ ) / y
式の両端が同じLである事から
cos ( 180-θ ) / -x = cosθ / x
-cos ( 180-θ ) = cosθ
sin ( 180-θ ) / y = sinθ / y
sin ( 180-θ ) = sinθ
という式が成り立つ。
tan ( 180-θ ) = -tanθ も同様に
tanθ = y / x
y = x * tanθ
tan ( 180-θ ) = y / -x
y = -x * tan ( 180-θ )
-x * tan ( 180-θ ) = x * tanθ
-tan ( 180-θ ) = tanθ
という式が成り立つ。
単純に
sin ( 180-θ ) = sinθ
cos ( 180-θ ) = -cosθ
tan ( 180-θ ) = -tanθ
で覚えてしまっても良いが、このように図で理解をしておけば、公式を忘れてしまっても同様の図を描く事で導き出す事が出来る。
まとめ
行列の計算はこの問題に限らず、午後試験の選択問題で基準点測量を選択すると必要になるので、覚えておこう。
また、この問題は午前試験の中では解き易い問題なので、三角関数をしっかりと身に着け、サクっと解答出来るようにしておこう。
今後も、モチベーションが続くうちは解説を投稿していきたいと思っている。
次回以降も、読んでいただけると有り難い。
ありがとうございました。
最後までお読み頂き有難う御座います。モチベーション維持の燃料にサポートいただけると有り難いです。
