【測量士補資格試験】円弧の延長

測量士の八重樫です。こんにちは。

測量士補の資格試験で出題される点数の取りやすい問題について
【測量士補資格試験】簡単な計算問題で点を稼ぐ
で、解説をした。
出題頻度が高くない為、上記のnoteでは解説しなかった問題をひとつ解説する。

簡単な計算問題でより多くの点数が取りたいという方は、上記リンクのnoteを買っていただけると有り難い。

円弧の延長

図 26－1 に示すように，点Ｏから五つの方向に直線道路が延びている。
直線 AO の距離は 400 m, 点A における点 O の方位角は 120°であり，直線 BO の距離は 300 m, 点Ｂにおける点Ｏの方位角は 190°である。
点 O の交差点を図 26－2 に示すように環状交差点に変更することを計画している。環状の道路を点Ｏを中心とする半径 R=20 m の円曲線とする場合，直線 AC，最短部分の円曲線 CD，直線 BDを合わせた路線長は幾らか。最も近いものを次の中から選べ。
ただし，円周率π =3.142 とする。
なお，関数の値が必要な場合は，巻末の関数表を使用すること。

　　1. 584.4 m
　　2. 677.5 m
　　3. 684.4 m
　　4. 686.2 m
　　5. 724.4 m
（ 平成30年 測量士補資格試験問題集 No.26 ）

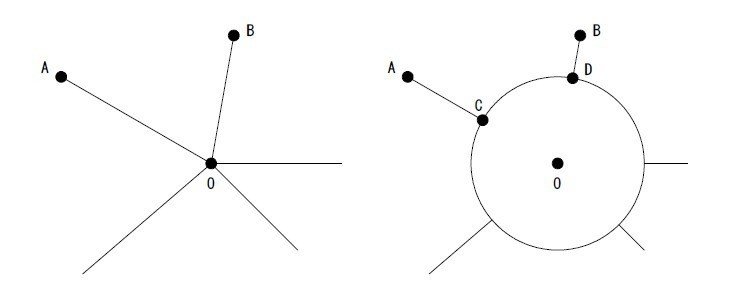
この問題は、円弧の延長を求める問題だ。
問題文から、直線ACと直線BDの距離は簡単に求められる。

直線AC = 直線AO - 半径
　　　  = 400 - 20
　　　  = 380

直線BD = 直線BO - 半径
　　　  = 300 - 20
　　　  = 280

円弧CDの距離を求める為に先ず角度AOBを求める。

190° - 120° = 70°

次に円周を求める。

円周 = 2πR
　　 = 2 ✕ 3.142 ✕ 20
　　 = 125.68m

円弧CDの距離は、円周全長の 70°/360° なので

円弧CD = 125.68m ✕ 70°/360°
　　　  = 24.43m

直線ACと直線BD、円弧CDを足す。

380m + 280m + 24.43m = 684.43m
　　　　　　　　　　　  = 684.4m

よって、正解は3だ。

まとめ

特に何の撚りもない、単純な問題だ。

測量士補の資格試験では、このように簡単に解ける計算問題も出題される。
こういった問題で確実に点数を稼ぎ、合格点を取ろう。

出題頻度の高い簡単な計算問題を
【測量士補資格試験】簡単な計算問題で点を稼ぐ
で解説している。
こちらも是非読んで頂きたい。

ありがとうございました。