
【共有馬主・一口馬主・POG】データを使って馬選び【R・回帰分析】
0. 2022年募集馬(2022/6/12)追加
社台から2022年の募集情報が出たので適用してみました。今年も去年同様、ノーザンが高額馬を外厩で募集しているので上位はノーザンです。今年の東京ダービーのシャルフジンは残念でしたが、あそこまで行ってますので、力を入れてるってことでしょうか。
ちょっと高いけど、素直に上位馬に応募しようと思います。
1.はじめに
競馬を馬券を買うだけでなく、一口馬主やPOGで馬主気分になるという楽しみ方をしている方もたくさんいらっしゃるかと思います。
この場合、出資馬・指名馬をどう選ぶかが、ゲームの主題になるわけですが、今回は私がやってる社台グループオーナーズの地方競馬オーナーズでの馬選び方法をデータを使って検討してみました。
今回はRを使った回帰分析を応用します。
2.結論
社台グループオーナーズの地方競馬オーナーズで馬を選ぶときは次の1~5に当てはまる馬を選ぶべし!今年の募集馬が発表されたら1頭1頭評価していきたいと思います。
入厩予定先が「外厩」 又は、バイネームで予定先が決まってる
一口の募集価格が高い
販売元がノーザンファーム
誕生日は遅い方がいい
入厩予定先の競馬場が川崎
次節から、具体的にご紹介します。
3.内容
(1)目的
パンフレットの情報を元に稼げる馬とそうでない馬を判別する要因を探す。
(2)使用するデータ
パンフレットはPDFとして提供されます。残念なことに保護がかかってて普通にテキストのコピーをすることは出来ません。
(参考)2021年度募集のページ
パンフレットの記載内容なんかが年々変わってることを鑑みて2016年生まれ~2019年生まれの4世代101頭のデータを分析対象としました。
また、実際にいくら稼いでいるかはnet競馬から2022/3/26現在の情報を取得しました。
(3)手法
Deeplearningで画像評価したり、コメント評価できると恰好いいのでしょうが、データ量や保護がかかっててテキストができない事情を鑑みて諦めました。
ということで、手で拾える情報を元にしてシンプルな線形回帰やロジスティック回帰でやってみることにしました。モデル選択はAICで評価します。
(4)被説明変数
次の3種類の被説明変数を作成しました。
1.募集馬中の世代別獲得賞金ランク上位25%なら1、それ以外は0
2.募集馬中の世代別獲得賞金ランク上位50%なら1、それ以外は0
3.募集馬中の世代別獲得賞金ランクの正規分布のパーセンタイル値
世代別獲得賞金をベースにしたのは現役期間が長いほど賞金が多くなるため。
(ちゃんと計算していませんが)上位25%以上で収支トントンかなという感覚です。またデータ眺めてちょうど切りが良さそうだったのでモデル1は上位25%にしました。バイナリ変数なのでロジスティック回帰を使います。
賞金を回帰する形もやろうと思ったですが、賞金そのものを使うと異常値に引っ張られそうなので、世代別獲得賞金ランクから計算したパーセンタイル値(ExcelのNORM.S.INVで計算)をモデル3としました。これは連続変数なので線形回帰を使います。
x=世代別ランク ※トップは1
p=1-(xー0.5)/同世代の件数 ※1世代25件でトップは0.98
被説明変数=NORM.S.INV(p)※トップは2.05
⇒ 被説明変数は標準正規分布に従う潜在変数で、
これが賞金に比例するというイメージ。
(5)説明変数
北海道予定:多くの馬が予定入厩先に「北海道 or xx」と書かれるが、中には「xx」だけの馬もいる。北海道競馬はデビューが早いので「北海道」が付いてる方が仕上がりが早いことが期待される。
入厩先の競馬場:大井 or 川崎 or 船橋 が選択される。期待馬が行きやすい先があるか?またはレベルの問題で、レベルの低いところに行った方が稼ぎやすい?
予定厩舎あり:多くの馬は競馬場までしか決まっていないが、中には厩舎まで決まってる馬がいる。どういうプロセスで決まるかしらないが、調教師の方からアプローチをかけて獲得したとすると期待度高い?
外厩利用:(外厩)と書かれる馬がいる。外厩の方が坂路があったりと設備がいいので、これも期待馬の印?
一口価格:当然、値が高い方がいい?
販売元:社台、ノーザン、追分のいずれか。天下のノーザンか?ダートは社台の方がイメージもあるが果たして、、、
誕生日:1月1日から数えた日数÷100。募集馬の誕生日は1~5月だが、早生まれの方が仕上がりが早くて得?
他にも父馬の血統や種付け料、母馬の実績なんかも想定できますが、PDFからのテキスト抽出ができないことを鑑み、この辺は価格に集約されるだろうという割り切ってます。
(6)結果
変数(記号)の説明です。
被説明変数
Y1 :世代別獲得賞金ランク上位25%なら1、それ以外は0
Y2 :世代別獲得賞金ランク上位50%なら1、それ以外は0
Y3 :世代別獲得賞金ランクの正規分布のパーセンタイル値
説明変数
X1 :外厩予定 or 予定厩舎ありなら1、それ以外は0 ※1
X2 :一口価格(百万)※2
X3 :販売元=ノーザン
X4 :競馬場が川崎予定
X5 :誕生日(1/1からの日数/100)※3
※1 試行錯誤の結果、1変数にまとめた方が結果がよかった
※2 1件、価格120万で走らない馬が異常値になってたので価格を全体の平均値で上書きした
※3 他の変数とオーダーを合わせるために100で割ったが、必要なかったかもY1予測モデルのサマリ。AICが高くなるように変数を選んだ結果です。外厩 or 予定厩舎ありで高い馬を選ぶのが良さそうです。一口価格が対数はそうしたらAICが改善したため。
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.3965 0.6431 0.616 0.53757
X1 0.9135 0.5678 1.609 0.10770 外厩予定 or 予定厩舎あり
log(X2) 3.0593 0.9736 3.142 0.00168 ** 一口価格の対数続いて、Y2予測モデル。Y1モデルに「販売元=ノーザン」と誕生日が追加されました。誕生日は遅い方がいいようです。仮説とは逆でしたが、実力があるにも関わらず誕生日が遅いと地方に飛ばされる説が浮上してきました。社台グループはいろんな販路がありますが、地方オーナーズはおそらく最下層なので。
なお、expにしてるのはそうしたらAICが改善したから。※本当は線形性の確認をしたいのだがロジスティック回帰で線形性を確認する方法がわからず、、、
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.4296 1.0223 -0.420 0.67429
X1 1.6209 0.5700 2.844 0.00446 ** 外厩予定 or 予定厩舎あり
log(X2) 1.7236 0.8030 2.146 0.03184 * 一口価格の対数
X3 1.5769 0.8296 1.901 0.05734 . 販売元=ノーザン
exp(X5) 0.4916 0.3063 1.605 0.10853 誕生日最後にY3予測モデル。誕生日は効かないが競馬場=川崎が効いてきた。ランク下位で効くのかもしれない。リスク軽減にいい変数かも。
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.3412 0.2817 1.211 0.2287
X1 0.4984 0.2116 2.356 0.0205 * 外厩予定 or 予定厩舎あり
log(X2) 0.8478 0.3335 2.542 0.0126 * 一口価格の対数
X3 0.6274 0.3347 1.875 0.0639 . 販売元=ノーザン
X4 0.3153 0.2097 1.503 0.1361 競馬場が川崎予定もう一回Y1~Y3で、全部の変数を入れてみる。どのモデルでも符号は入れ替わってないことがわかる。
<Y1>
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.1679 1.1784 -0.991 0.32163
X1 1.1758 0.6181 1.902 0.05713 .
log(X2) 2.8266 1.0372 2.725 0.00643 **
X3 0.2115 1.1955 0.177 0.85956
X4 0.1789 0.5855 0.306 0.75997
exp(X5) 0.5251 0.3498 1.501 0.13335
---
<Y2>
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.5737 1.0431 -0.550 0.5824
X1 1.6372 0.5777 2.834 0.0046 **
log(X2) 1.6313 0.8185 1.993 0.0463 *
X3 1.6929 0.8401 2.015 0.0439 *
X4 0.4848 0.4979 0.974 0.3301
exp(X5) 0.4584 0.3120 1.469 0.1418
<Y3>
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.01063 0.43297 0.025 0.9805
X1 0.56040 0.22035 2.543 0.0126 *
log(X2) 0.80013 0.33687 2.375 0.0196 *
X3 0.64614 0.33517 1.928 0.0569 .
X4 0.28175 0.21235 1.327 0.1877
exp(X5) 0.12516 0.12449 1.005 0.3173 それぞれのモデルの出力結果の上位25%とY1と比較するとこんな感じ。
> p1 <- predict(glm(formula=Y1~X1+log(X2) ,family=binomial))
> table(p1 >= quantile(p1,0.75), Y1)
Y1
0 1
FALSE 65 10
TRUE 15 11
> p2 <- predict(glm(formula=Y2~X1+log(X2)+X3+exp(X5) ,family=binomial))
> table(p2 >= quantile(p2,0.75), Y1)
Y1
0 1
FALSE 65 10
TRUE 15 11
> p3 <- predict(glm(formula=Y3~X1+log(X2)+X3+X4))
> table(p3 >= quantile(p3,0.75), Y1)
Y1
0 1
FALSE 62 12
TRUE 18 9
> table(p1 >= quantile(p1,0.75) & p2 >= quantile(p2,0.75), Y1)
Y1
0 1
FALSE 70 13
TRUE 10 8
Y1予測モデルとY2予測モデルを組み合わせはいい感じ
> table(p1 >= quantile(p1,0.75) & p2 >= quantile(p2,0.75)
& p3 >= quantile(p3,0.75), Y1)
Y1
0 1
FALSE 71 15
TRUE 9 6
Y3予測モデルは上位25%の抽出には向いてない?
下位を加味した結果だということですかね。4.あらためて結果
(1)まとめ
上位25%を狙うにはまず↓が大事
入厩予定先が「外厩」 又は、バイネームで予定先が決まってる
募集価格が高い
次に見るべきは↓
販売元がノーザンファーム
誕生日は遅い方がいい
最後に
入厩予定先の競馬場が川崎
今年の募集馬はこの基準で選びたいと思います!
(2)2022年度デビュー馬の評価
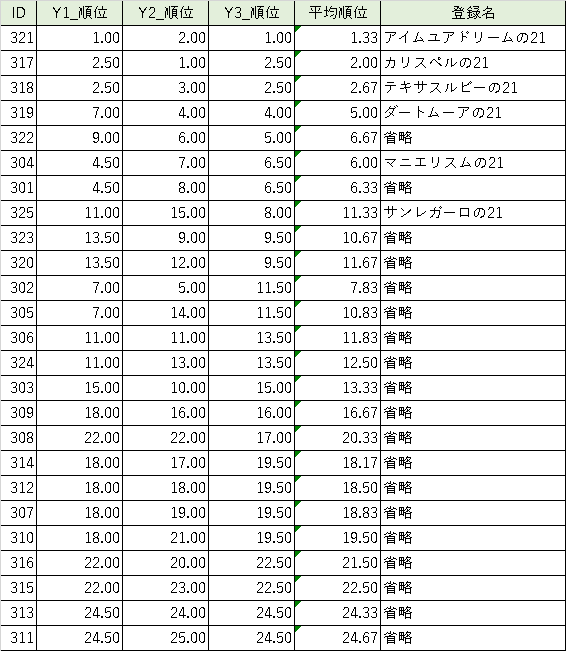
Y1~Y3のスコアとその順位は以下のとおりです。順位は同順の場合平均値を取ってます。
1位のメガクライトの20はサトノクラウン✕タキオンの血統でダートは良さそうです。
ノーザン馬がみんな「外厩or厩舎バイネーム」&「高価格」で上位です。地方競馬も賞金上がってきてるのでノーザンも力を入れ始めた?
馬名 Y1 Y1順位 Y2 Y2順位 Y3 Y3順位 順位平均
メガクライトの20 0.22 3.5 3.72 1 1.17 3 2.5
パーフェクトジョイの20 0.22 3.5 3.70 2 1.17 3 2.8
データの20 0.22 3.5 3.56 3 1.17 3 3.2
ローエキスキーズの20 0.22 3.5 2.75 5 1.17 3 3.8
シャーペンエッジの20 0.22 3.5 3.34 4 1.17 3 3.5
ナターレの20 0.22 3.5 1.31 8 0.86 7 6.2
アルフォンシーヌの20 -0.81 8.5 2.45 6 0.89 6 6.8
ショコラヴェリーヌの20 -0.29 7 0.93 10 0.47 8 8.3
ゴールデンロッドの20 -0.81 8.5 1.69 7 0.26 10 8.5
ミラグレの20 -1.49 13.5 1.15 9 0.07 12 11.5
ディミータの20 -1.49 13.5 0.23 13 0.39 9 11.8
ダイナミズムの20 -1.49 13.5 0.81 11 0.07 12 12.2
ボンバルリーナの20 -1.49 13.5 0.36 12 0.07 12 12.5
ブローザキャンドルの20 -1.17 10.5 0.01 15 -0.09 14.5 13.3
スアデラの20 -1.17 10.5 -0.52 18 -0.09 14.5 14.3
ハッピーウェーブの20 -1.72 17 0.02 14 -0.24 18 16.3
ブラックアテナの20 -2.41 21.5 -0.08 16 -0.11 16 17.8
グラッブユアハートの20 -1.72 17 -0.56 19 -0.24 18 18.0
フライングバルーンの20 -1.72 17 -0.80 21 -0.24 18 18.7
エクレアオールの20 -2.41 21.5 -0.31 17 -0.43 22 20.2
マニエリスムの20 -2.41 21.5 -0.85 22 -0.43 22 21.8
バーボネラの20 -2.41 21.5 -0.87 23 -0.43 22 22.2
シュクルダールの20 -2.41 21.5 -1.17 24 -0.43 22 22.5
エイブルインレースの20 -2.41 21.5 -1.23 26 -0.43 22 23.2
オーバーレイの20 -2.82 26 -0.69 20 -0.54 26 24.0
オッティマルーチェの20 -2.82 26 -1.43 27 -0.54 26 26.3
ビーチマリカの20 -2.82 26 -1.58 28 -0.54 26 26.7
ワカチナの20 -3.29 28 -1.17 25 -0.67 28 27.0
5.おまけ
(1)検証の補足
Y3予測モデルで価格が線形に効いてるかをチェックしてみました。対数とると線形性がアップするようです。


(2)Rのコード
大したことやってませんがご参考
# ファイル読み込み
X <- read.table("ファイルパス", sep="\t", header=F)
attach(X)
# 変数定義 ヘッダーOFFで読み込んだのでデフォルトでV~という変数名が付いてる
# V1 賞金
# V2 ランキング
# V3 上位25%
# V4 上位50%
# V5 上位%
# V6 累積逆
# V7 誕生日
# V8 北海道予定
# V9 大井予定
# V10 川崎予定
# V11 船橋予定
# V12 外厩予定
# V13 予定厩舎あり
# V14 一口価格
# V15 社台
# V16 ノーザン
# V17 追分
Y1 <- V3
Y2 <- V4
Y3 <- V6
X1 <- V13 + V14 # 補足 V13とV14は元々排他だったので、+はorと同じ意味
X2 <- V14
X3 <- V16
X4 <- V10
X5 <- V7
# ララベルの19の価格を補正
X2[X2==1.2] <- X2[X2==1.2] <- mean(X2[X2!=1.2])
# モデルのサマリ出力
summary(glm(formula=Y1~X1+log(X2) ,family=binomial))
summary(glm(formula=Y2~X1+log(X2)+X3+exp(X5) ,family=binomial))
summary(glm(formula=Y3~X1+log(X2)+X3+X4))
# 線形性の確認
r1 <- residuals(glm(formula=Y3~X1+X3+X4+exp(X5)))
r2 <- residuals(glm(formula=X2~X1+X3+X4+exp(X5)))
plot(r2,r1, xlab="X2の残差", ylab="Y3の残差")
lines(lowess(r2,r1))
# X2を対数にしてリトライ
r2 <- residuals(glm(formula=log(X2)~X1+X3+X4+exp(X5)))
plot(r2,r1, xlab="log(X2)の残差", ylab="Y3の残差")
lines(lowess(r2,r1))以上
