深さ優先探索とモンテカルロ法

トイプロブレムといわれるような前提条件がしっかりと明記できる物事を数理モデル化したあと、（現実で起こっているものは前提条件を明記することが極めて難解であることをフレーム問題という）

分岐によって、ゴールへの最短距離を把握したい。（→こういうのを「モチベーション」という）

＜迷路の場合＞

＜ハノイの塔の場合＞

では、将棋・以後において探索はどのようなことになるのか？

将棋：９＊９の盤で駒が8種類、かつ獲得した駒が使える→10の220乗通り
囲碁：19*19の盤で駒が白黒→10の360乗通り

観測可能な宇宙全体の水素原子の数は約10の80乗個。なのですべて調べるのは不可能。

ここで登場するのが深さ優先探索
最短距離ではないかもしれないが、適正のある解をみつけることができる。
では、どうやるのか？具体的にはMiniMax法というのを用いる。

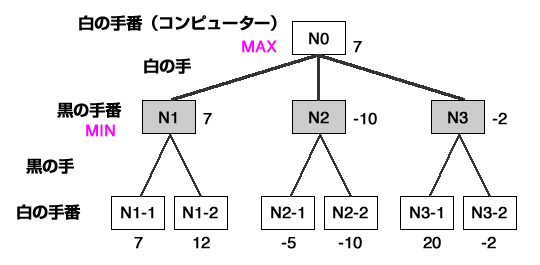
コストを設定し、自分がさすときにスコアが最大。相手がさすときにはスコアが最小となるように評価し他の物を切る（これをαβ法という）

で、スコアをどう評価するのか？以前までは、人間の手でやっていたがこれを解消するのが、モンテカルロ法

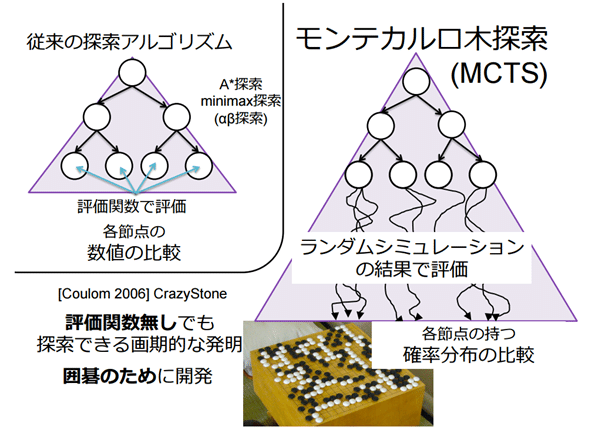
一定のところに来たらランダムシュミレーションを発生。
確率分布を用いることにより、スコア評価を立てる。

＜感じたこと＞
モンテカルロ法は直接民主制な感じ。
でも、これができるのは一つ一つの碁が同じ重さであるという前提のもと成り立つ。

僕はあまり直接民主制が好きではないのは、政治におけるパフォーマンスにとって本当に人間は重みづけしなくていいのかというのが疑問であること

また、それと人権は本当に同じなのかも疑問。
「平等」と「公平」は共存できるのか？資本主義と民主主義の両立はAI化が進むにつれてどのように変容するのかは関心があります。