
確率計算でデッキを最適化しようとする話
超概要
デッキ枚数や各カードの採用枚数を確率計算を用いて最適化しようとした試みを紹介します。予め定義した理想的な手札になる確率を最大化するようなデッキ構成を提案するツールを作成・公開しています!
導入
マスターデュエルがきっかけで遊戯王に復帰して以来、主に召喚シャドールとヌメロンデッキを組んでいました。その中で「どのカードを何枚入れたら手札事故が起こる確率を最小化できるんだろう🤔」と考えることが幾度となくあったのですが、実際にデッキを回して試行錯誤しながら最適化をしていました。
エクシーズフェスティバルも無事完走できましたし、素引きしたくない札が多いDD音響セフィラを調整していることもあり、今回真面目に確率計算の観点からデッキを最適化する方法を考えてみました!また、主に自分で使う向けではありますが、デッキ最適化ツールを作成・公開したので、それについても触れられればと思います。ぜひ最後まで読んでいただけると嬉しいです😁
想定読者
そんなわけで、今回のブログは以下のような方々に向けて書いたつもりです。
感覚に頼らないデッキ構築に興味がある方
TCGにおける数学について興味がある方
遊戯王をきっかけに高校数学やプログラミングを勉強したい方
(そんな人いるのか?)
せっかくなので数学が絡んだ話もするつもりではありますが、「$${x}$$とか$${y}$$とか見るだけでもしんどい😨」という方は具体例の章まで飛ばして読んでいただけると!
基本的な考え方
デッキを最適化すると大きなことを言いましたが、手札の強さやそこから成立する盤面を定量的に評価するのはかなり厳しいので、今回は「与えられた条件を満たす手札を初手で引ける確率が最大になるようなカード及びデッキの枚数を提示する」というアプローチで考えてみました。
…と抽象的なことを言ってもよく分からないと思いますが、PSYフレーム・ドライバー素引き問題だと思ってくれれば遊戯王プレイヤーには分かりやすいと思います。ドライバーを素引きする確率を最小化しようと思ったら、ドライバーをピン刺ししてデッキを60枚にすれば良いですが、それだと3枚までしか入れられないγを引く確率も下がってしまいます。要は、γを引ける確率とドライバーを引いてしまう確率はトレードオフの関係にあるわけです。それならば、「40~60枚のうちのどこかに、γを引く確率を高めながら、ドライバーを引いてしまう確率を下げることができるデッキ枚数が存在するのではないか?」というのが本記事での基本的な考え方です。
「γを引くメリットとドライバーを引くデメリットの大きさは同じじゃないでしょ👎」という至極真っ当なご意見が聞こえてきますが、いきなり難しい問題を考えても仕方がないので、ぜひそのあたりをうまく定量化するアイディアをいただければと思います🙏

(γ3積みできたのは太古の昔ですが、遊戯王プレイヤーに課題感に共感してもらうための例なのでご容赦ください🙏)
計算式
数学のお時間です(と言っても高1レベルですが)。いきなり複雑なパターンの数式をポンと出しても説明しづらいので、最初にカード1種類をドローする確率の計算式を解説してから、複数種類に一般化した式について説明したいと思います!
カードが1種類のみの場合
まずデッキ枚数を$${N}$$、カード1のデッキ投入枚数を$${m_1}$$とします。それが初手手札$${H}$$枚の中にちょうど$${h_1}$$枚存在する確率は以下のように書けます。
$$
\frac{{}_{m_1}\mathrm{C}_{h_1} \times {}_{N - m_1}\mathrm{C}_{H - h_1}}{{}_{N}\mathrm{C}_{H}}
$$
いきなり数式だけ出されてもナンノコッチャだと思うので、噛み砕いて説明したいと思います。(ちなみに、$${\mathrm{C}}$$は組み合わせを表す記号です)
まず分母部分ですが、こちらは単純明快で「$${N}$$枚あるデッキの中から$${H}$$枚カードを引いたときの組み合わせの数」を表しています。読んで字の如く$${{}_{N}\mathrm{C}_{H}}$$になりますね。
一方、分子部分は2つに分かれていて、前半部分が「デッキに$${m_1}$$枚入っているカード1を$${h_1}$$枚引く組み合わせの数」を表しています。考え方は分母部分と同じですね。そして、後半部分が「カード1以外のカードで残りの手札を作ったときの組み合わせの数」を表しています。カード1以外のカードはデッキに$${N - m_1}$$枚あって、残りの手札は$${H - h_1}$$枚なのでこのような形になります。また、前半後半の事象はカードが異なるため独立なので、単純にかけ合わせれば「手札$${H}$$枚のうち、カード1を$${h_1}$$枚引く場合の数」が求まるわけですね。
そして、最後に条件を満たす場合の数を全ての手札が取りうる場合の数で割れば、求めたい確率になります。これが最もシンプルなパターンの式になります。
念の為具体例を出すと、40枚デッキに3積みしてあるγが初期手札5枚の中にちょうど1枚ある確率は、
$$
\frac{{}_{3}\mathrm{C}_{1} \times {}_{37}\mathrm{C}_{4}}{{}_{40}\mathrm{C}_{5}} = 0.3011...
$$
となり、約30%であることが分かりますね。
カードが複数種類の場合
次に、カード1, 2, …, nと複数のカードで手札を作る場合に一般化してみましょう。考え方は同じで、デッキに$${m_i}$$枚入っているカード$${i}$$を$${h_i}$$枚引くときの場合の数は$${{}_{m_i}\mathrm{C}_{h_i}}$$と書けることを念頭に置けば、以下の式のようになります。
$$
\frac{1}{{}_{N}\mathrm{C}_{H}} \times \prod_{i=1}^{n} {}_{m_i}\mathrm{C}_{h_i} \times {}_{N - \sum_{i=1}^n m_i}\mathrm{C}_{H - \sum_{i=1}^n h_i} \\ \text{where} \sum_{i=1}^n m_i \leq N , \sum_{i=1}^n h_i \leq H
$$
ゴチャゴチャしてちょっと分かりづらいかもしれませんが、落ち着いて考えれば意外と簡単です。
まず、第一項目は1種類のときの分母と同じなので良いとして、第二項目はカード1, 2, …, nのそれぞれ$${m_i}$$枚入っているカードを$${h_i}$$枚引く場合の数を表しています。カードごとに場合の数を計算してそれらを全部かけ算する($${\prod}$$は累乗の記号)ことで計算ができます。
そして、第三項は1種類のときの分子の後半部分と同じで、もしカード1, 2, …, nで手札が$${H}$$枚にならず、デッキの残りのカードで手札を埋めたときの場合の数を表しています。
where以降はこの式が成立する条件ですね。とは言っても、カード1, 2, …, nのデッキ投入枚数の総和はデッキ全体の枚数以下でなければならないとか、カード1, 2, …, nそれぞれの手札枚数の総和は手札全体の枚数以下でなければならないとか、まあ当たり前のことですね。
こちらでも念の為数式を出してみます。40枚デッキに3積みしているγを1枚、1枚積みのドライバーが0枚に手札に来る確率を求める計算式は、
$$
\frac{{}_{3}\mathrm{C}_{1} \times {}_{1}\mathrm{C}_{0} \times {}_{36}\mathrm{C}_{4}}{{}_{40}\mathrm{C}_{5}} = 0.268…
$$
と約26.8%なり、先程のγを1枚のみ引く確率が30%だったのと比べるとドライバーを素引きしてしまった場合の分確率が下がってしまっていますね。
最適化方法
前項で説明したように色々な条件のカードを引く確率を計算することができました。今度はこの計算式を使ってどのようにデッキ枚数や各カードの採用枚数を最適化するかを説明します。
色々なアプローチがあるとは思いますが、遊戯王はデッキ枚数が40~60枚の制約があるおかげで探索空間はさほど広くないため、条件を満たす全てのデッキにおいて理想的な手札をドローする確率を計算して、一番確率が高かったデッキ構成を提示するという力技で解決することにしました。
今後もっと複雑なケースに対応しようとして、計算時間が長すぎるなど問題が発生した際には、より良い計算方法を考えたいですねー
具体例
ここまで数式と文字ばかりが続いて飽き飽きしているとは思いますので、ここからは具体的な話をします。計算式の項を頑張って読み切ってくださった方、ありがとうございます🙇
この章では、まず冒頭で挙げたドライバー素引き問題を確率の観点で最適化する簡単な例について話した上で、ヌメロンデッキを題材にして実際の最適化例について計算結果を紹介します!
ドライバー素引き問題
γを3枚、ドライバーを1枚それぞれ採用し、γを1枚、ドライバーを0枚ドローする確率をデッキを40~60枚の間で変化させながら計算したものをグラフにしたものが下の図になります。
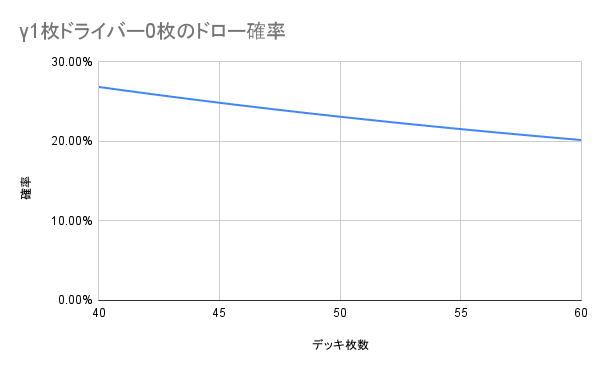
ぼくも意外だったのですが、40枚デッキが最も理想的な手札になる確率が高いデッキであることが分かりました!おそらく、デッキ枚数を多くしてドライバーを素引きする確率を下げても、γを引けなくなるインパクトの方が大きいことを意味しているのだと考えています。
ヌメロンデッキの最適化
今度は前回のブログでも紹介した勝率8割超えのヌメロンデッキをより最適化してみましょう。
(構築記事です。もし良ければこちらもどうぞ)
まず、理想的な後攻時の手札6枚は、
手札誘発: 2枚以上
初動札: 1枚以上
バック除去: 1枚
モンスター無力化: 1枚
ダイレクト: 0枚
と仮定します。後攻からどんなデッキ相手でも捲くろうと思ったらこんな感じの配分だと戦いやすいだろうという考えです。
そして、これを投入するデッキの要素としては、
手札誘発: 6~20枚
初動札: 3~13枚
バック除去: 3~8枚
モンスター無力化: 3~6枚
ダイレクト: 2~3枚
があり得るとします。この範囲は一応具体的なカードをイメージして書いていますが、カード名を出すとキリがなくなってしまうので、こういう設定なんだと思ってください🙇♂
そして、これを後述する最適化ツールに突っ込んで見ると以下のような結果になりました!
デッキ枚数: 40枚
手札誘発: 17枚
初動札: 9枚
バック除去: 6枚
モンスター無力化: 6枚
ダイレクト: 2枚
理想手札確率: 13.20%
これだけ多数の条件があると、全てを満たす確率はどうしても低くなってしまいますが、基本的にはデッキを40枚にしつつ、手札に来てほしい比率に合わせて採用すれば良いことが分かります。
「ヌメロンなのに誘発より初動札が少ないってどういうこと😡」という声が聞こえてきますが、これがカードの重要度を加味できていない弊害ですね…とは言え、初動札を入れすぎると今度は捲り札が引けず結局負けてしまうので、初動札を可能な限り入れれば良いというわけではないことが伝わればいいと思っています。今後もっといい最適化方法を考えていきたいです💪
ツールの紹介
最後になりますが、今回の実験にあたってPythonのツールを自作して公開してみました。
プログラムがよく分からない方でもDockerをインストールして、上のページにある例に沿って設定ファイルを作成して実行すれば簡単に使えます。
既に使い勝手の部分で改良の余地ありと思っているので、適宜アップデートとしたいなと考えています!(時間が取れればですが…)
あとがき
「デッキ調整は試行錯誤に時間がかかるから、プログラムでサクッとできるようにしたい!」と思って考え始めましたが、ついでに仕事で中々触れなかったGitHub Actionsなんかも活用できて満足しています☺
次のネタはチェーンバーンかDD音響セフィラのどちらかにしようと思っていますが、両者ともさほど独自性がないため、書きごたえがないかもなとぼんやり考えています。では、またどこかで👋
この記事が気に入ったらサポートをしてみませんか?
