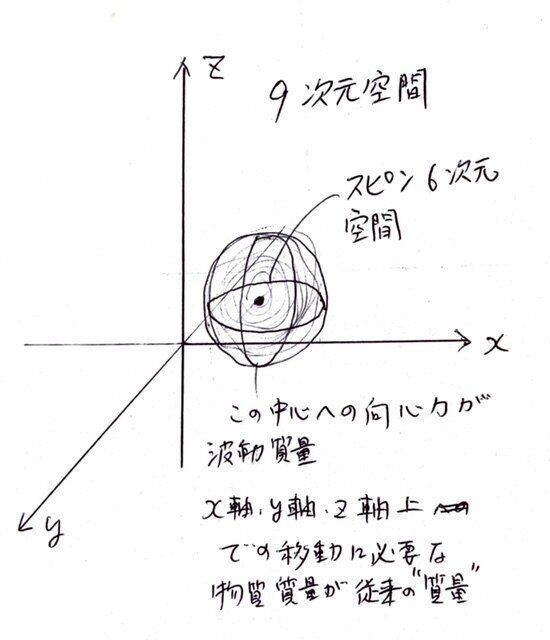
スピンと９次元

1つの平面スピンには1つの軸がある。空間に1つのスピンが生成されると1つの軸が同時に生じる。このことにより空間に直線である軸(x軸)が生成される。ここではスピンを単純な回転運動体としておこう。

言い換えればスピンによって座標軸は生まれるともいえる。
1つのスピンはそのスピンが存在する平面（2次元）も同時に定義する。このため1つのスピンが合計3次元を構成していることになる。
このことと　体積を要求する物体に3次元でその寸法（外形など）を表示できることは一致している。

ただ3次元といってもそれぞれの軸を絶対的に固定表示しているわけではなくないので不定3次元といっても良い。おなじみのXYZ直交系も空間のなかではどうにでも回転できるから絶対系ではなく原点の位置も絶対的には定まらない。要するに３成分の変数だけでは空間内の絶対的位置は表示できない。
このような不定3次元では原点を1つ定めた上での相対的位置を座標表示できるが、絶対的な空間中の地点を示しているわけではない。あくまでも原点に対しての相対的な位置を表示すると言うまでである。

空間内に絶対的な位置を割り振るには１）原点と少なくとも2本の直交座標または、２）3本の直交座標を固定して定義する必要がある。
空間における絶対的座標点を定めるには3次元XYＺ座標系を固定しなければならないがどうすればいいのか。そちらの方から考えるとこれらのｘ軸ｙ軸ｚ軸にスピンの輪っかをはめる事が考えられる。

不定直交座標系（3成分）をスピン運動平面座標系（6成分）と組み合わせれば全空間を固定し絶対座標系を組み立てることができるだろう。スピン平面は不定直交座標系とは独立して定義できる平面座標とする。これはXYZ座標系に従属して生ずるx-y平面などとは別のものである。

また全ての運動は直交するスピン３成分の線形結合和として書けるだろう。ここではスピンもまたベクトル演算と同様に扱えると思う。ややこしい空間らせん運動もこの書き方が合うかもしれない。単位スピンのベクトル風演算化についてはまた別稿で述べたい。また平面座標という考え方についても別に述べたい。ここでは要点だけ述べておく。

座標軸は直線であり目盛りは点である。面座標は面自体が座標となる面である。目盛りに相当するのがスピンである。ここではそのひとつのスピンがひとつの点単位に相当するから直線の長さなどは意識されない。点がその縦横径など無視されているのと同様である。スピンのもつ基本物理量は半径と角速度である。

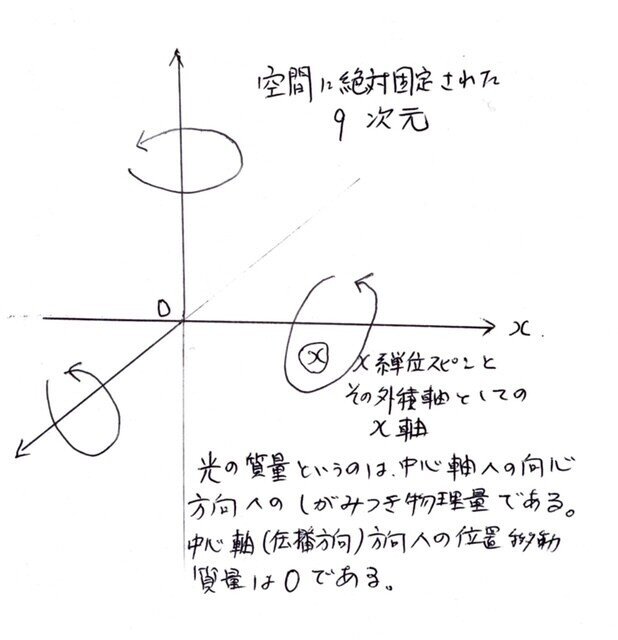
スピンは実物次元となる。スピンが規定するxyz軸に相当するものが面である。スピン面次元も3成分ある。我々はx-y , y-z, z-x 平面といいそうであるが、それとは異なる。単位スピンに分解してもそれは動的、現実の座標成分である。xyz軸３次元は不定、imaginaryなもので空間に自由な方向、自由な目盛り尺度で設定できるが、スピン平面次元は実座標である。空間内の任意のスピンは単位スピン３成分に分解して考えることができる。直交する３平面への投影図と同じである。空間スピン平面は２次元でひとつの絶対成分である。これがそれとは直交する法線軸を定義するためひと方向へ３次元、３方向で９次元の空間を定義できることになる。

光は空間内のエネルギー伝搬現象である。物体移動は伴わないから仕事はしなくてよい。勝手に伝搬するのだ。音に質量を求める方もいないだろう。波動というのは波動中心軸へのしがみつき（束縛）によって生じるわけだから、波動に質量を求めるならば、波動中心軸への向心力をFとした時、Fを角加速度で割ったものが波動質量である。

私の説の場合、光の質量は振動軸への束縛性が質量に相当する物理量（波動質量）であり、拡散伝搬方向への質量は０である。言い換えれば９次元座標上は光のもつ仕事能力はスピン平面座標成分内にあり（光のエネルギーはスピン振動数のみに比例）その伝搬は勝手に生じるのでエネルギー伝搬の仕事は０でよい。物体を運ぶには仕事が要るがエネルギーのみを運ぶには仕事は要らない。

勝手に生じる：伝搬を阻害するものがなく反作用を受けない。従って加速度がない。光のエネルギーが物体に当たって、そこに光が当たったと観測された瞬間もうそこには光はない。