場は空間の歪みによって生じる

円、正方形を斜めから見ると楕円、台形に見える。台形というのは遠近感による。

円を斜めから

正方形を斜めから

半径がaの円の面積はπa²  一辺が2aの正方形の面積は4a² だから

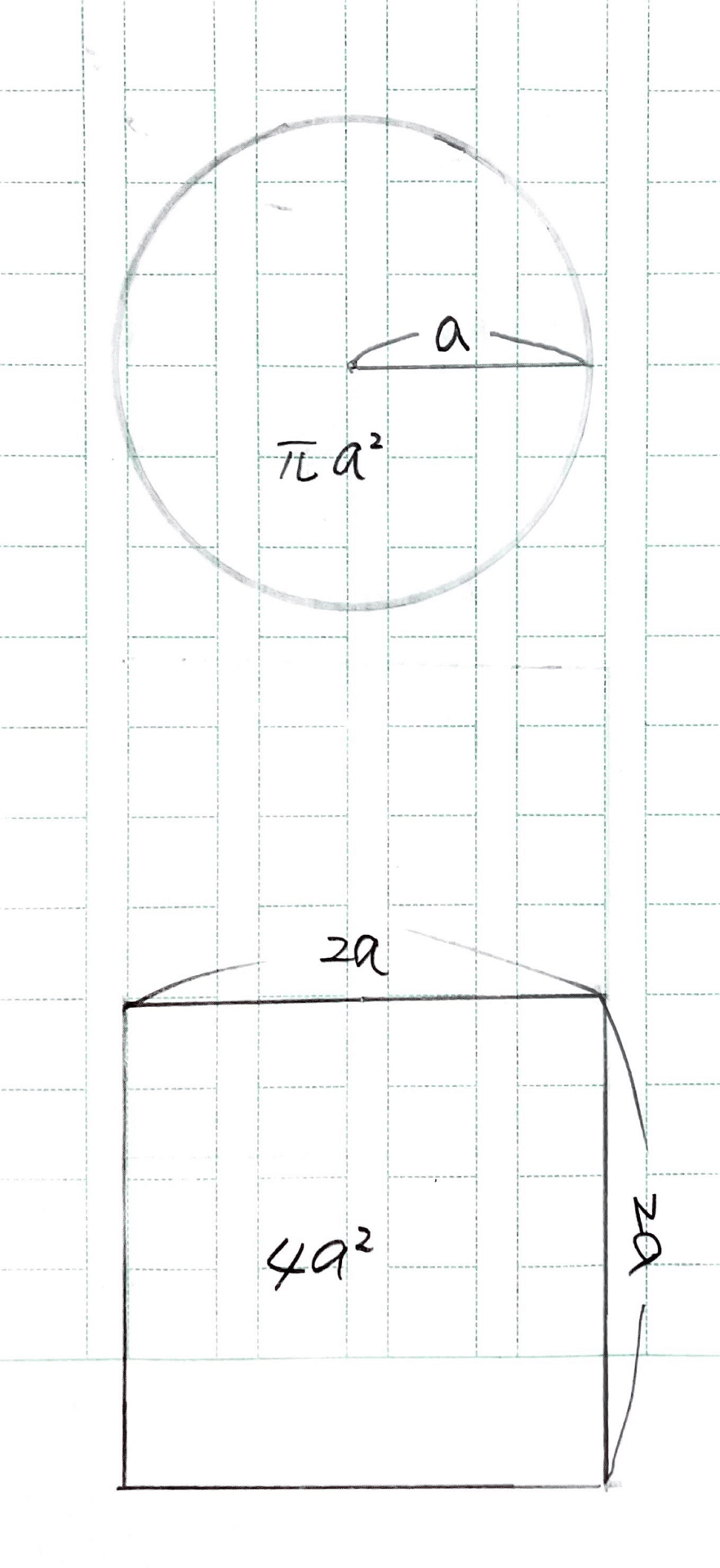
この正円と正方形の面積比はπ:4である。
これらを斜めから見たときの写像を考える。遠近感を除外して考えるとする。
見ている方角にとってその見る方向を縦、それとは直交する方向を横と表現する。
横方向には長さの変化はないが、縦方向が縮んで見えるのが写像だ。
円の半径が縦方向にはa→b  に縮んだとする。正方形は縦方向にやはり同率で縮むから横の辺が2aならばその縦の辺は2bとなる。
この時の見かけ上の正方形の面積は長方形の面積となり4abとなる。
写像だから縮んで見える面積比が変わるはずはないから楕円とと長方形の面積比はπ:4のままなのでそれぞれの面積はπab ,  4abということになる。これは公式からみても一致している。
つまり同角度からの写像をとっても平面図形の面積比は変化しない。
話は飛ぶが、太陽系の惑星は楕円軌道をとる。ケプラーの第一法則。
これは惑星が誕生した時の初期運動量が保存されているからその方向成分が振動していると考えられる。
もし初期運動量が0ならば正円軌道であるはずなのだ。
仮にY成分の運動量がX成分の運動量のμ倍ならばY成分の振動は
Y =μsinθと書ける。
X =cosθ ならば
X² +(Y/μ)²=1
これは楕円の式である。
こう考えると初期運動量の存在というのは軌道の正円を歪ませていることになる。
従って運動量というのは空間の歪みのひとつの表現形態だとも言えるだろう。
物体の歪みがバネだと言うならば空間の歪みもまた一種のバネである。これを"場"と呼ぶのだ。
ポテンシャルというのは場の歪みの程度のこととも言える。