二次試験における電験一種特有の問題と解き方(機械制御)
電験一種二次試験は、当然ですが電験二種の延長線上にあるため、二種の知識だけで解ける問題も沢山あります。しかし、そうは言っても、一種特有の問題はあります。
そこで電験一種二次試験の特有の問題の紹介と、その解法について書いてみたいと思います。
また、逆にそれ以外の問題は二種の知識で解ける問題となるので、二種受験者の人で二種の問題が尽きた人は、腕試しで解いてみてはいかがでしょうか(問題の年度は記事内で紹介します)。
それでは、まずは機械制御から本記事で説明します。
0.概要
誘導機、同期機、変圧器から2問、パワエレから1問、自動制御から1問出題されます。
ほとんど計算問題が出題されており、構成は2種と同じです。
ただし、二種は変圧器と誘導機の出題割合が高いですが、一種は同期機の出題割合が、近年は多くなっています。
昔は静止器として、高潮波フィルタ等も出ていました。
また、「同期ワットで表したトルク」という用語が一種の誘導機と同期機で頻出して出ますが、この用語は単に二次入力のことです。
以下、同期機、誘導機、変圧器の出題表

それでは、以下各単元ごとに、説明しています。
1.誘導機
二種の時の時には出なかった、以下の計算問題が出てきます。
(ア)二次励磁電源接続
(イ)誘導発電機(回生制動)
(ウ)二重かご形誘導電動機
(エ)単相誘導電動機
誘導機単独の出題表です。その他の問題は二種の知識でもある程度は解けると思います。
(ア)~(エ)の一種特有の問題は、あまり捻った問題は出ていないので、知っていれば得点源です。

(ア)二次励磁電源接続
下記のような回路図が与えられます。電源が二次側に挿入されていることが特徴です。過去の出題周期を見ても、そろそろ出題される頃合いな気がします。
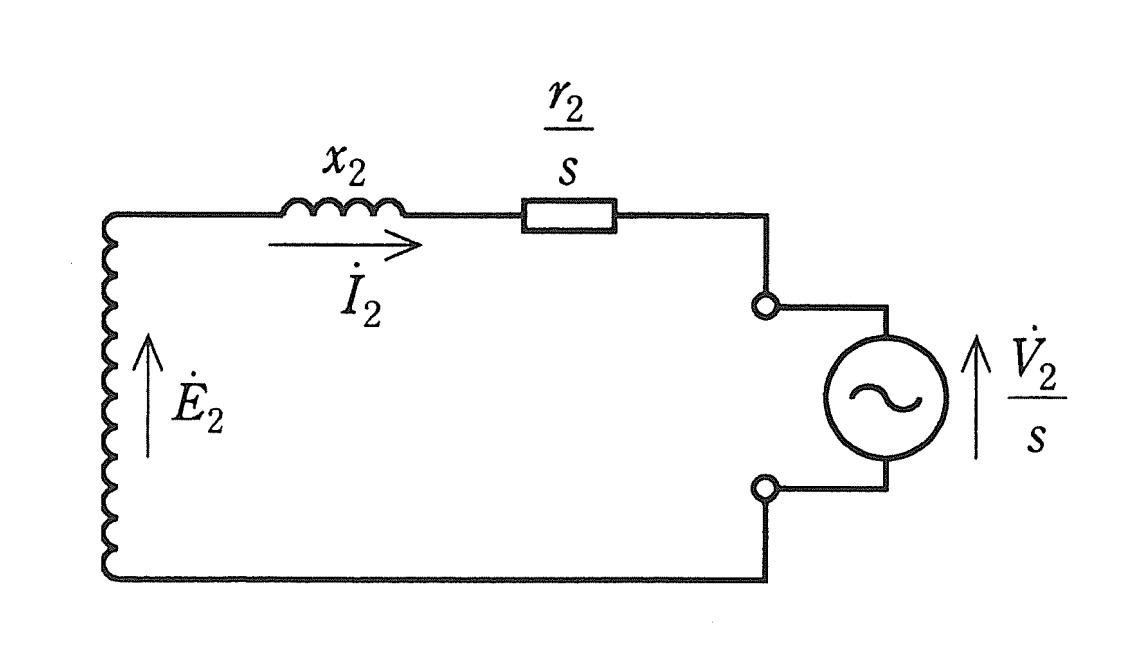
上記の回路図を分解して、下記のような回路図と考えると分かりやすいかと思います。

問題で問われる数値と求め方は、下記の4つです。

上記の4つの求め方を覚えておけば、ある程度対応できると思います。
(イ)誘導発電機(回生制動)
二種でも一次試験で頻出なので、ご存じの方も多いと思いますが、誘導機の滑りsが負の時、電動機ではなく発電機として働きます。
回路図は通常の誘導電動機と変わりません。


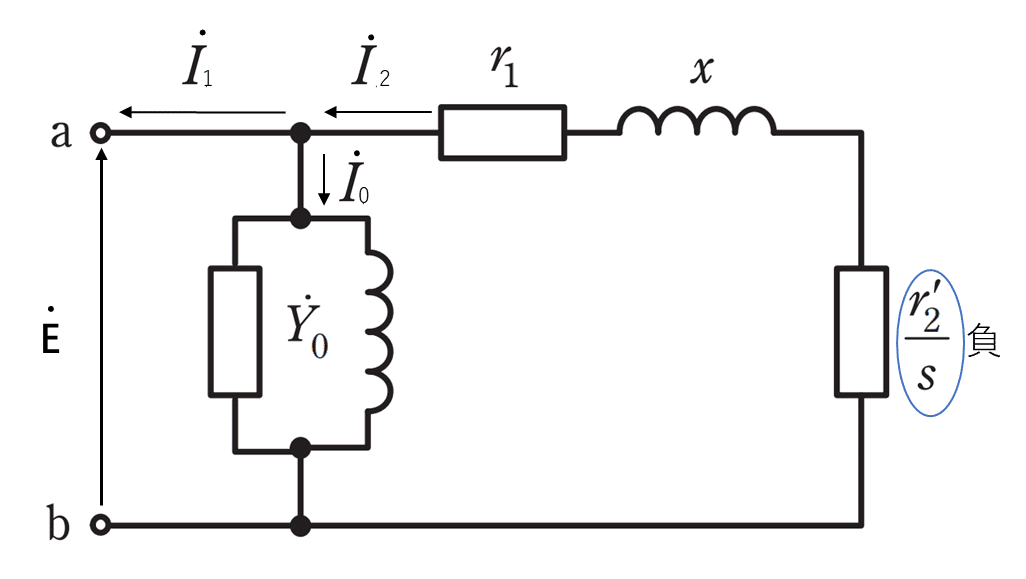

(ウ)二重かご形誘導電動機
こちらも二種一次試験で必須の項目。過去2回出ていますが、どちらも計算が軽いため、知っていればサービス問題だと思います。
回路は下記となります。

この問題は滑りsおよび抵抗・リアクタンスが既知の元で、出力(orトルク)を求める問題となります。解答の手順は下記となります。

注意すべき点は②の実部がR/sであることです。文字式だと分かりやすいですが、実際の数字であった場合、ついつい滑りsで割っていることを忘れがちになり、④のRにR/sの数値を代入するミスを私はよくしていました。
(エ)単相誘導電動機
過去一度しか出ていませんが、若干特殊な部分があるため取り上げます。
回路図は下記となります。

過去の出題としては
①回路Bの滑りsnを求める(=2-s)
②回路全体のインピーダンスZを求める。
③回路全体を流れる電流I1を求める
④等価回路Aの二次電流Ip2を求める
※等価回路Bの二次電流はxm/2が大きいためIと見なせると仮定。
⑤同期ワットで表したトルクT(二次入力)を求める。
と出題されていました。
②~④は回路に基づいて、素直に求めていけば求まります。
⑤については、二次入力のため、Iの2乗にr/(2s)を掛ければ求まるのですが、Bは反対方向にトルクが発生しています。
つまり、求め方としては、下記となります。

2.同期機
二種の同期機の問題は円筒形のみ出題されていますが、一種では突極機が出題されることがあります。数年前まではほとんど円筒形の問題でしたが、令和3年度、令和5年度と短い周期で出題されましたので、今後は突極形メインになる可能性もあると思います。
以下出題表です。
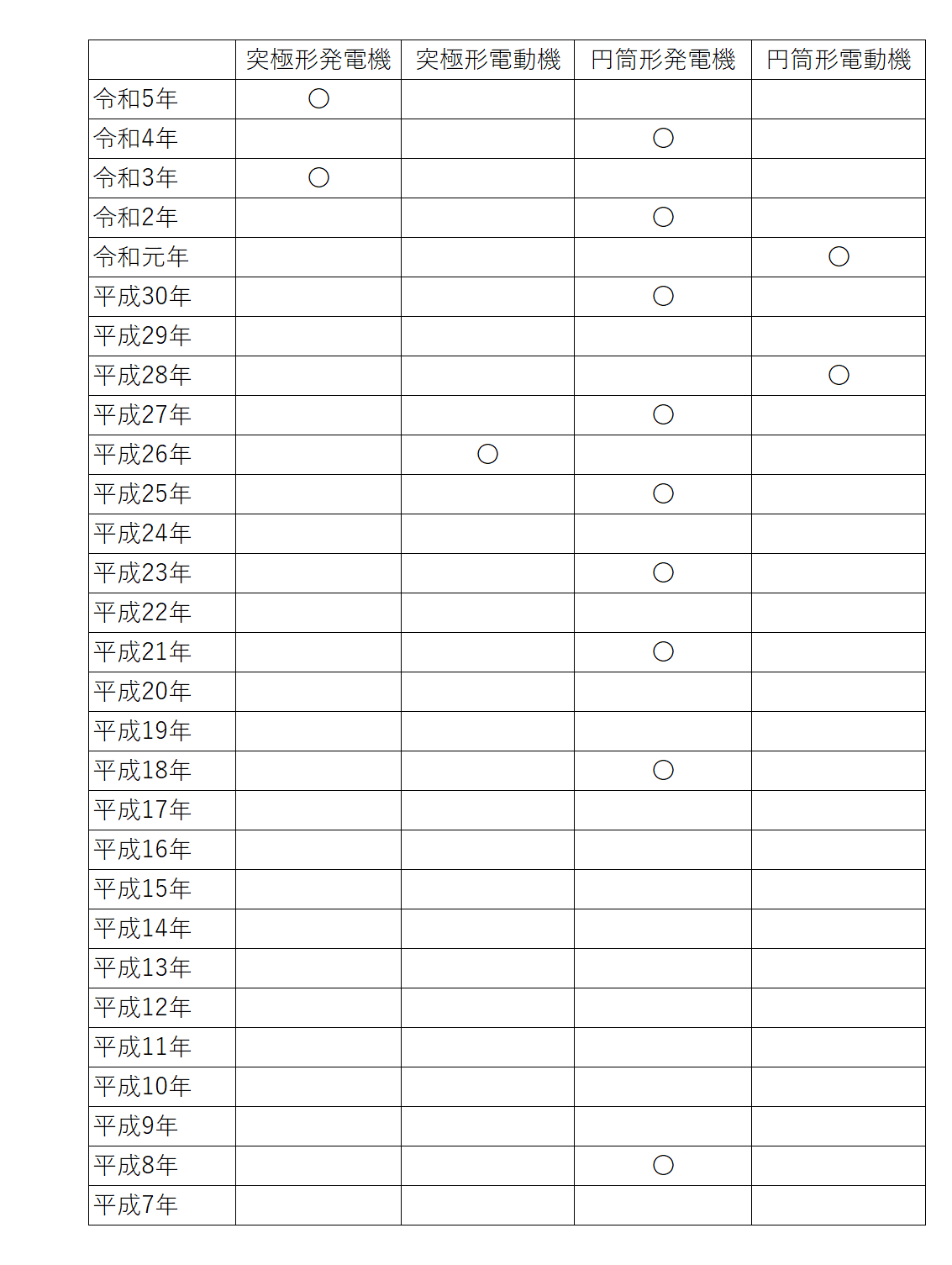
円筒形の方は二種の知識でほぼ解けると思いますので、突極形の発電機に絞って説明したいと思います。
突極形の特徴としては、リアクタンスが横軸リアクタンスXqと縦軸リアクタンスXdの二つの種類があることす。なお、Xd>Xqとなります。
それに伴い、当然フェーザ図も変わってくるのですが、フェーザ図の表し方が二通りあります。
令和5年度はフェーザ図を書く問題が出題されたのですが、令和3年度の出題とは違う方で指定されていましたので、両方学ぶ必要があります。
実際に出題・解答となったフェーザ図は下記となります。


図1の方はリアクタンスに直接電流Iを掛けて電圧降下を求めていますが、図2の方は電流を横軸電機子電流Iqと縦軸電機子電流IdをそれぞれXq、Xdに掛けて電圧降下を求めています。
なお、図2のようにIを分解する関係で、基準ベクトルは誘導起電力Eとします。
問題としては、無負荷誘導起電力Eを求める問題が多いです。解答の方針は、それぞれ下記となります。
(ア)図1:令和3年度出題の図

赤枠の三角形と青枠の三角形が相似であることを利用します。
V、φ、Xq、Xd、Iが既知として、
①三角比を利用して、緑色の三角形のV以外の各辺を求める。
②jXqIを求める。
③三平方の定理を利用してEqを求める
④jXd-jXqから青色の三角形の一辺を求める。
⑤三角形の相似を利用してEを求める。
(イ)図2:令和5年度出題の図
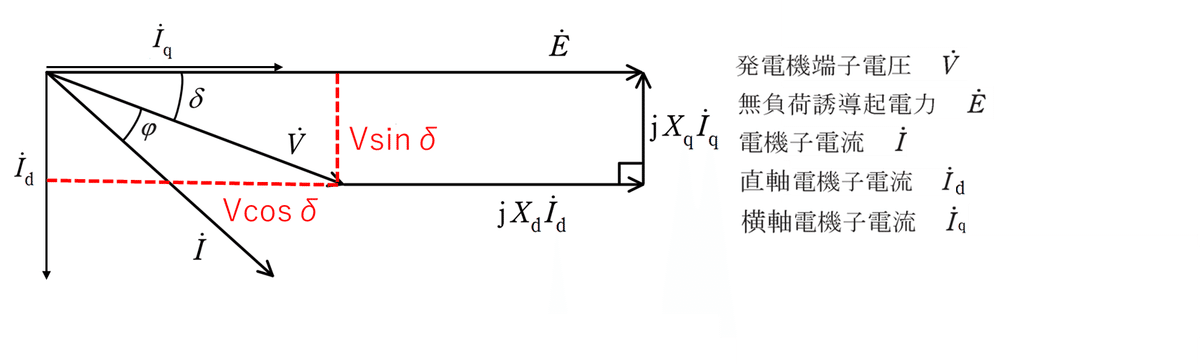
上手のように発電機端子電圧VをVsinδとVcosδに分解します。
すると、実軸方向と虚軸方向に着目すると下記の二つの方程式が成り立ちます。
①虚軸方向:Vsinδ+XqIq=Vsinδ+XqIcos(φ+δ)=0
②実軸方向:Vcosδ+XdId=Vcosδ+XdIsin(φ+δ)=E
最初に①の虚軸方向を計算して、未知数を求めて、その後に②実軸方向の式に①で求めた値を代入する方針を立てると、割と思考をすっきりさせて進めれるのではないかと思います。
図1と図2の使い分けについては、基本は問題文の誘導があるので気にしなくてもよいかもしれませんが、図1の方は負荷角δが未知数、図2の方は力率角φが未知数となります。
力率角φが未知であると、図1の緑色の三角形の辺の長さを求められないためですね。
以上で、突極形同期発電機だけでしたが、同期機の説明を終わります。
なお、同期機では抵抗を無視する問題が多いですが、抵抗を考慮する場合計算が複雑になる傾向がありますので、当日の問題選択の方針の一つになるのではないかと思います。(私は抵抗を考慮する場合は、問題の選択を極力避けたいと思っていました。)
3.変圧器
ほぼ全ての問題が二種の知識で解けるのではないかと思いますが、一種っぽい箇所を私の偏見で2つ記載します(二種の知識でも解ける箇所とは思いますが)。
(ア)電圧変動率
変圧器の電圧変動率εの解法としては二種では

で求めることが一般的かと思いますが、一種では

で求めることが、多いです。
しかし、この式も問題文で与えられたり、この式自体を求める問題が出題されているため、覚えていなくても解けると思います。
また、この式は2種でも一度出題されています。
上記の式が登場するのはR2、H24
(イ) 周波数、電圧の変動に伴う鉄損の変動
周波数f、電圧Vが基準から変化した際に、鉄損がどのように変化するかの問題です。
鉄損Pfはヒステリシス損Phと渦電流損Peに分けられますが、それぞれ下記のように比例します。

二種の二次試験では出題されていなかったと思いますが、二種一次試験でも出題されたことがあるため、今後二種でも出題される可能性があるとは思います。
過去出題されたのは、H26、H17
4.自動制御
一種から現代制御も頻繁に出題されます。とはいえ、古典制御の方が割合が高く、特に最近は古典制御ばかり出ているので、傾向の変化を感じます。
以下、古典制御と現代制御の出題表です。

(1)現代制御
現代制御は二種では一度しか出題されていませんので、勉強する前は身構える人が多いかもしれません。しかし、出題自体はパターン問題が多いので、一度解法を覚えてしまえば得点を取りやすいと思います。
以下、現代制御での頻出事項です。

上の①~④は初見では意味が分からないと思います。しかし、実際の問題と解答を見たら分かると思いますので、解きながら体で覚えるのが一番早いと思います。
最近の問題ですと、H27年問4(1)~(3)で上記の①~③が、H25問4(1)で上記の①③④が解けます。
その他の問題は問題文の誘導に沿ったら解けると思います。
(2)古典制御
多くの問題が二種の知識で解けるとは思います。
一種特有の問題だと感じたのは、ラウスの配列表を用いて、安定限界を求める問題です。(二種の出題は安定となる条件を求めるまでかと思います)
とはいえ、特に難しいところはなく、下記の配列表の3列目が0となる場合を求めるだけです。

安定限界であるとき、bc-ad=0
また、この時2行目に着目してbs^2+d=0が成り立ちます。
以上、機械制御について、私が一種と二種との違いを感じた部分を抽出・説明してみました。二種の勉強した人は、意外と二種と変わらないのではと思ったのではないかと思います。
実際、私は三種⇒二種⇒一種と勉強を進めたのですが、三種⇒二種よりも、二種⇒一種の方が学ぶことは少なくて済むと感じました。(もちろん人によって感じ方は変わるとは思いますが)
さて、次回は同様に電力・管理について投稿する予定です。電力・管理分を投稿できれば、私が話したかったことも一通り話せて満足なので、電験に関する投稿も次回が最後にしようかなと思っています。ではでは。
この記事が気に入ったらサポートをしてみませんか?
