
モンティ・ホール問題を、根性で解く。
突然ですが、皆さんは「モンティ・ホール問題」をご存じでしょうか?
モンティホール問題は条件付き確率に関する問題で、正解が直感に反することから「モンティホール・ジレンマ」とも呼ばれています。
モンティホール問題とは
以下のようなゲームを考えます。
0. 三つの扉A,B,Cがある。一つは正解。二つは不正解。正解の扉の向こうにはスポーツカーがあり、正解を当てることが出来ればスポーツカーをもらうことが出来る。不正解のドアの向こうにはヤギがいるが、特に意味はない。

1. プレーヤーは、三つの中から一つ扉を選ぶ。

2. 司会者(モンティ)は答えを知っており,残り二つの扉の中で不正解の扉を一つ選んで開ける。
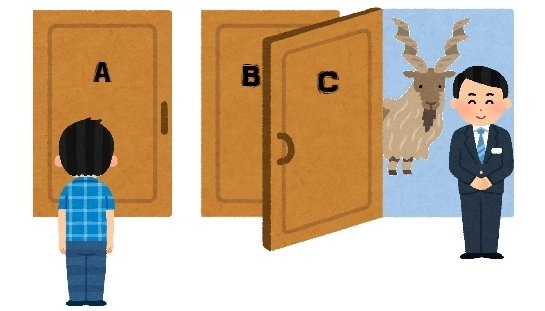
Q.プレーヤーは残り二つの扉A,Bの中から再度好きな方を選べる。
このとき、プレーヤーは選んだ扉を変えるべきか?変えないべきか?
この問題の答えについて、多くの人はこのように考えます。
2.の時点で閉じている扉は二つ。
ここから、いずれか一方にある正解の扉を選ぶので確率は1/2、
つまり、扉を変えようが変えなかろうが、確率は同じだ。しかし、実際には正解は下記のようになるそうです。
扉を変えない場合に正解する確率は1/3、
扉を変えた場合は正解する確率が2/3になるので、
扉を変えた方が良い。
…おいおい、ちょいと待てや、あんちゃん。いくらオイラに学がねえからって人を騙すのは感心しねえなあ。後から選んだモンを変えただけで当たる確率が上がるって?そんなこつ、あるわけないわいな!
と言うわけで、全然納得できないので実験して確かめてみることにしました。
実験の概要
三枚のトランプを用意する。一枚は♥(赤)、二枚は♠と♣のカード(黒)とする。
以下の手順でゲームを行う
出題者は三枚のカードをシャッフルし、伏せて場に出す。
回答者は場にあるカードのうち一枚を選ぶ
出題者は『回答者が選んでいない』カードのうち、黒のカードをいずれか一枚めくる
回答者は「選んだカードを変更するか、そのまま変更しないか」を選択する
回答者は選んだカードをめくり、♥のカードであれば成功。
これを、「回答者が選んだカードを変更する」パターンと「回答者が選んだカードを変更しない」パターン、それぞれ10回施行し、成功の回数を確認する。直感的には、いずれも正解が$${\frac 1 2}$$になる気がするが、果たして…。
実験の様子
カードを変更する。1回目
👨、三枚のカードをシャッフルして伏せて場に並べる。

👩「うーん、どれにしようかなあ。よし、右側のカードを選ぶぞ!」
👨「では、真ん中と左側のカードから、黒いカードを一枚めくりますね」

👨「では、選んだカードを変えますか?変えませんか?」
👩「うーん、どうしよう…。よし!変えます!左で!」
👨「.。o(必ず変えるんだけどなぁ…。)」

👩「やったー!当たったー!」
カードを変更する。2回目
👨、三枚のカードをシャッフルして伏せて場に並べる。

👩「うーん、どれにしようかなあ。よし、揺るがないこの気持ち!右側のカードを選ぶぞ!」
👨「では、真ん中と左側のカードから、黒いカードを一枚めくりますね」

👨「では、選んだカードを変えますか?変えませんか?」
👩「うーん、よし!変えます、変えます!やっぱ左で!」
👨「.。o(必ず変えるんでしょ?)」

👩「やったー!当たったー!」
カードを変更するんだってば。3回目
👨、三枚のカードをシャッフルして伏せて場に並べる。

👩「うーん、どれにしようかなあ。よし、こんどは右側のカードを選ぶぞ!」
👨「では、真ん中と左側のカードから、黒いカードを一枚めくりますね」

👨「では、選んだカードを変えますか?変えませんか?」
👩「即決!変えます!左!」
👨「.。o(必ず変え)」

👩「やったー!当たったー!」
~中略!~
カードは変えない。1回目
👩、三枚のカードをシャッフルして伏せて場に並べる。

👨「うーん、どれにしようかなあ。よし、右側のカードを選ぶぞ!」
👩「では、真ん中と左側のカードから、黒いカードを一枚めくりますね」

👩「では、選んだカードを変えますか?変えませんか?」
👨「男に二言はない!変えません!右!」
👩「.。o(変えないの決まってるのにな。)」

👨「ギャャー!ハズレたー!」
カードは変えない。2回目
👩、三枚のカードをシャッフルして伏せて場に並べる。

👨「うーん、どれにしようかなあ。よし、右側のカードを選ぶぞ!」
👩「では、真ん中と左側のカードから、黒いカードを一枚めくりますね」

👩「では、選んだカードを変えますか?変えませんか?」
👨「よし、やっぱり初志貫徹!右で!絶対、変えません!」
👩「.。o(いや、どうせ変えないんでしょ?)」

👨「ギャャー!ハズレたー!」
~以下略!~
実験の結果
さて、そんなこんなで進めた実験の結果をまとめたのが下表となります。

やばッ!なんか、やってる感じの結果になっちゃった!なんと、かなりはっきり、「カードを変更した方が成功確率が高くなる」という結果が得られました。少なくとも、「確率は$${\frac 1 2}$$である」とは言えなさそうです。
考察
どんなアホでも茶番を10回も繰り返してると気がつきます。「あれ?カードを変更しないなら、3.以降の手順って意味なくね?」と。
そう。カードをめくらない場合、最初の選択で♥を選ぶ確率$${\frac 1 3}$$がそのままゲームの成功確率$${\frac 1 3}$$となるわけで、何もしないのに確率が変わる、ましてや高くなる($${\frac 1 2}$$)なんてことは起こるわけがないのです。
一方、めくるカードを変える場合、4の手順で「必ず最初に選んだカードではない色が選択される」ことになるので、成功となるのは、最初に選んだカードが♣か♠だった場合であり、その確率は$${\frac 2 3}$$です。最初に♥を選んでいたときのみ失敗するので、失敗の確率は$${\frac 1 3}$$になります。
まとめ
1990年のアメリカで、頭のいい人、マリリン・ヴォス・サヴァントが、自身の雑誌連載のコラムでモンティホール問題を紹介したところ、大炎上するという事件がありました。
1990年9月9日発行、ニュース雑誌「Parade」にてマリリン・ヴォス・サヴァントが連載するコラム「マリリンにおまかせ」で、上記の読者投稿による質問に「正解は『ドアを変更する』である。なぜなら、ドアを変更した場合には景品を当てる確率が2倍になるからだ」と回答。すると直後から、読者からの「彼女の解答は間違っている」との約1万通の投書が殺到し、本問題は大議論に発展した。
答えをめぐっての騒動
投書には、1000人近い博士号保持者からのものも含まれていた。その大部分は「ドアを変えても確率は五分五分(2分の1)であり、3分の2にはならない」とするものであった。サヴァントは投書への反論を試み、同年12月2日、数通の反論の手紙を紹介した。
・ジョージ・メイソン大学 ロバート・サッチス博士「プロの数学者として、一般大衆の数学的知識の低さを憂慮する。自らの間違いを認める事で現状が改善されます」
・フロリダ大学 スコット・スミス博士「君は明らかなヘマをした(中略)世界最高の知能指数保有者である貴女が自ら数学的無知をこれ以上世間に広める愚行を直ちに止め、恥を知るように!」
赤っ恥をかいたであろう数学者達に共通しているのは、「実際に試してみなかった」ことではないでしょうか。言うて、$${\frac 1 2}$$か$${\frac 2 3}$$かの話なので、我々のようにせいぜい20回もやってみれば少なくとも「$${\frac 1 2}$$じゃないかも」ということには気がつくでしょうし、100回も繰り返せばかなりはっきり確率が解ることになるでしょう。
一方マリリンは、その後、コラム連載三回分を使って反論したにもかからわらず、全く解ってもらえずにボコボコにされたそうです。彼女は、手を替え品を替えて説明を繰り返していたようですが、案外、こう一言、言い返してやれば良かったのではないでしょうか?
「そんなに言うなら、実際にやってみたらいいじゃない?」、と。
おまけ
ちなみに、実験はゆる学徒カフェで行いました。
ノンアルコールヘビーユーザー、濃くておいしかったです。

