
今日からフラクタル構造で相場が面白くわかるようになる。
こんばんは。
MYBです。
今夜は、フラクタル構造のまとめ記事にしていこうと思います。
誤字・脱字は指摘されて手直ししていきますので誤字脱字を発見しましたら、、、お教えください。
このnoteを始めるきっかけになったのも、「出来高の手法」を公開し、
その本来の手法の1部と公開してきましたが、本来の手法の第2弾のルールのようなものがこのフラクタル・・・
(※この記事も長いですができる限り重要部分を切り抜いて解説を心掛け
できる限り最低限伝えたい事を伝えていこうと思います。)
この記事で、少し「本来の手法」に1歩近づけるんじゃないかと思います。

その間にも記事更新してきましたが、、、この1つ前「記事の心理(フラクタル)細部」記事も含めまとめていきます。
まずは
全記事の続きから、今回のあらすじはこうです。
1つの手法があり、
そのエントリーPOINTの高値や安値でのPOINTでエントリーを行う手法を公開 その際に値幅トレードが人気がありましたので
①N値計算を主軸にしてN値計算再現しながら出来高の手法をプラスしていき公開してきました。
②今回で、フラクタルも使用してN値計算軸のMTFフラクタルというものを参考に行えるトレード内容を公開してきました。(YOUTUBE)
②のフラクタルについての基礎+応用ガイドをnoteで記載してこの記事では
フラクタルを相場から効率よく見つけられるような
YOUTUBE上で基礎ガイド動画をアップしていますのでよろしければご覧ください。
今書いてる段階で、、どこまで短くまとめきれるか、、不安ですが、、
走り始めたので、進みますw
この記事を読んで諦める人が半分くらいになりそうですが、、理解すると結果は面白いくらいフラクタルに興味をわいてもらえると思います。
実際に生徒の中にもフラクタルと言われるものが見えるようになってから11連勝とか勝率が格段に上がってきます。
相場の本質事態を感じれるって思えるようになり、テクニカル分析に磨きがかかります。
勝てるようになるには、知らなくて損する事はあっても、知って損する事なんか1つもありませんので(^^♪
斬新に、話していくように努めます!!
きっと貴方も相場を見るのが楽しくなりますよ♪
フラクタルという知識をまず色々な視点、色々な環境から認識していきましょう。
まずは基本に入ります。
フラクタルとは
・フラクタルとは、形の適宜な一部を取ってもそれが全体と似ている成り立ちをしていること。自己相似的。
・幾何学概念:フランスの数学者ブノワ・マンデルブロが導入
ラテン語の fractus から。図形の部分と全体が自己相似(再帰)になっているものなどをいう。
自然界から我々はいつの間にか、このフラクタルと言われる常識を生活の1部にフラクタルは存在します。
よくシェルピンスキーガスケットの三角形なんかは1度は耳にしたりネット上で見たことがある思います。
この図形は極端に理解しやすい図で誰にでも理解しやすいように表されている内容です。
これを参考に視点を変えるだけで、自然界にも同じような現象の山の形、木の形、葉の形なんかは私たちの正解の1部として溶け込んでいると思います。
この場合、シェルピンスキーガスケットと同じ手順でそれぞれの縮小コピーを縮小率や縦横比が深い関係を構築しており、まさにこの下記の動画は、
相場にも当てはまる内容となります。
こういった自然界でのフラクタルと言われる現象を、イギリスのルイス・フライ・リチャードソン(気象学者)がスペインとポルトガルの国境線の987㎞・1214㎞の縮尺から、それぞれ縮尺と国境の長さが対数を取ると相関に関係する事を発見した事から世界中に知れ渡った。この事から、身近な物にもフラクタルが存在することがわかるようになる。
この発見から、マンデルブロが名付け親になってマンデルブロ集合なんかは
一種のデザインにもなっている。(拡大画像を見るわかると思う)

なんかオシャレじゃないですか???ww(こんなスカーフありそう)
このフラクタルには定義できる計算式も、もちろん存在する。
基本的な内容と相場の視点等はこちらから↓ご視聴の上ご確認ください。
ではここから裁量トレードに磨きをかける思考を持つ為に知って置きたい
知識を書き込んでいこうと思います。
差分方程式 =漸化式
このフラクタルの自己相似関係式(再帰式)にはある変数に依存して決まる値またはその対応を表す式として一般認知され数の集合として値(数値)の集合写像の一種と理解されている。
この幾つかの集合からそれぞれに取った元の組に応じてその集合1つの元に定める対応関係である。
幾何学とこのシェルピンスキーガスケットの関係と認識していて私はこの関係を相場にはめ込む作業も1つの視点としてフラクタルと言われる内容の一種としても捉えております。
この上記内容をもとに動画を見ていただけると、、、理解が深まると思います。
差分方程式と使用される例(下記画像)

ロジスティック写像A

上記画像は見たことはある方もいらしゃると思います。
しかし、、、今まで話してきているフラクタルにも、、絶対はなく
しばしば非常に複雑なカオス的は挙動を作りあげられるときも、もちろんあります。
相場でも同じですし、自然界でも同様である。
(例)たまに珍しい形の野菜や、相場でも今までの波形形成を無視する瞬間に起きる相場の環境が指標や発言、急騰、急落で起きてしまう自動決済などが起きると、1つのシーンとしても今までと全く異なる相場環境に変化してしまう時が存在する。(カオス的 非線型分析学を見てもらうと理解しやすいかもしれませんが、手法解説から外れるのでここでは割愛します。)ことはありますが、基本的な知識はフラクタルとして分析していく計算方程式です。
余談だが、、、
余談だが、、、私の分析で公開使用しているフィボはこの差分方程式の計算式と深く関係があり、、、次回の記事にこの計算式なども含め詳細内容も、、、話していきますが
フィボを使用して、今までN値計算に特化して、動画配信している事には意味があり、フィボナッチ数列の計算式には
上記の差分方程式縦型を初期値に置きこの数列の仕組みの理解が深まるわけです。ただ、、、適当に当てはめてるわけでは、、、ありませんよ?ってことだけお伝えしておきます。
今日は、、このフラクタルを利用して、縦ではなく横の話をしていきます。
次回がフィボを利用して、、、縦だよ!って事です。
話が飛んでしまいましたので、、、戻ります。
ロジスティック写像で表現
ロジスティック方程式は
y=y0L÷y0+(L−y0)e−kt
という微分方程式で表される。N は個体数、t は時間、dN/dt が個体数の増加率を意味する。r は内的自然増加率、K は環境収容力と呼ばれる定数である。個体数が増えて環境収容力に近づくほど、個体数増加率が減っていくというモデルになっている。
これを相場に当てはめていきます。
N=相場参加者 T=時間経過時間(波形形成されるまでの時間)
として表現します。
式の解(相場参加者と時間の関係)はS字型の曲線を描き、個体数は最終的には環境収容力の値に収束する。
この曲線や解の関数はロジスティック曲線やロジスティック関数として知られる。
方程式の名称は、ロジスティック式やロジスティックモデル、ロジスティック微分方程式と表記される場合もある。
ロジスティック方程式は、個体群生態学あるいは個体群動態論における数理モデルとしては入門的なものとして位置づけられ、より複雑な現象に対応する基礎を与え数学分野としては、微分方程式論や力学系理論の初等的な話題としても取り上げられる。
フラクタルが起きる計算式を見てさっぱりという方に、ロジスティック画像
をもとに画像で表して無理やりフラクタルとどう関係があるのか理解しやす
く画像だけで解説していきます。(できているかは、、、うーん・・・けど理解しやすいと思って例えます。)
上記の画像Aは、分岐図でX軸をずらしていくと形に変化が起きます。
上から下に、X0,6を下の0,2に動かしたときの図をイメージしてください。
横から見たときに丸み帯びている図の位置が下に下がるイメージが作られると思います。
この流れが、、相場の流れ(例えば1日の流れと考えてください)
画像B

こんなイメージ図になっていれば正解です。
ではここから、この流れの途中に起きる現象を思考してください。
この流れの中にすべての形が同じになる瞬間があります。
画像C

この上記画像を見てもらえればイメージわきますか???
イメージする事が重要ですので、、、イメージは行うようにしてください。
このフラクタルが起きる計算式ってこういうフラクタルが起きる計算式としてまず、、、今は、、、感じるだけで結構です。。。
数学の勉強をしていくわけではありませんので。
(聞いた事も見たこともない方もお読みになっていますのでこの内容を詳しい方はノークレームでお願いします。)
こんな感じと捉えてもらえるだけで大丈夫です。
大きな流れの中に起きる小さな同じ現象があると感じてください。
ロジステック方程式の離散化から学ぶ
この曲線はそもそも・・・どういった内容で知られたのか簡単に話していきます。
人口論における方程式でピエール=フランソワ・フェルフスト(ベルギー出身)が最初の発表者。
(はい!ここまでで、フラクタル相場と、、、どう関係あるんだ!!という気持ちはまず抑えてください。)
ピエール=フランソワ・フェルフスト(P/F/F)は
ある環境における生体個体数の時間変化を表す為に発表されたもので次式で表される。
ここまで来て、、、少し感が良い人はお気づきかもしれないが、、、過去の出来高の動画内の解説でティックの内容が、相場参加者という言葉を選択したり、、、この増加や数値を常にトレーダーの種別として大口とか表現してきた事に結びついてくる事が???理解できてくるだろう・・・(多分)
曲線形状からわかる事
今からは、計算式を掲載しても結局、、、相場のMT4に当てはめて理解していくほうが早く理解しやすいはずなので、図で理解しやすく進めていきます。
この計算式を調べればわかるが、人口論における研究がメインだった事から、この記事ではこの人口の関係数値を出来高や相場の参加者として、損切り退場者・利確退場者として表現したいと思い、取り上げています。
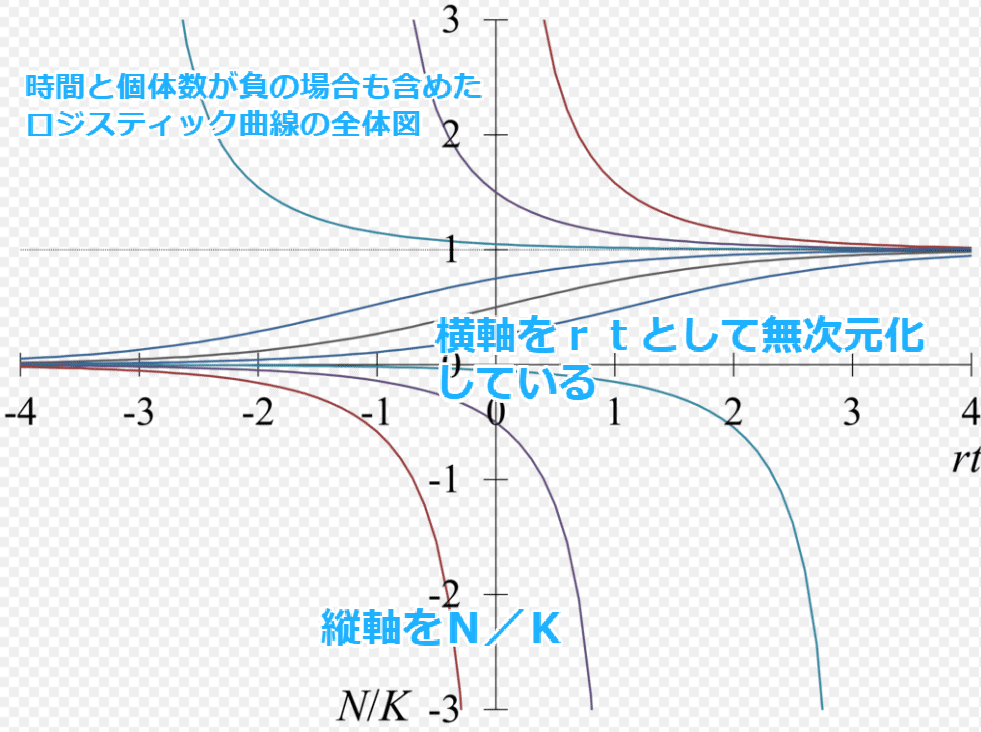
横軸をT(時間)縦軸をN(値幅(数値変動))として考えいく。
画像D

この数本のロジスティック曲線だが、N>0の範囲では、時間経過とともに
NはKに収束していく事がわかる。
勿論、収束後は拡大していく。全く相場と同じなのである。
レンジ⇒ブレイク⇒保ちあい⇒レンジの中の
ブレイクから保ちあいのシーンを上記 画像D で表現。
この曲線収束が上記の 画像C のフラクタルになる瞬間と、相場状況でいうと、保ちあい相場の感覚を今回の記事では、、、示していきます。
画像C

以上の仕組みから
画像F
上記のような相場環境も起こりえる。
(※有料ページで、リトレースを使用して再現解説を行います。)
そのほかの参考イメージ画像を動画内から参照

Nの環境収容力が半分以下になっているとき、初期状態の点(t=0、N=N0)から始まる曲線はゆっくりと右肩上がりに上っていく。
Tの増加につれて、曲線の傾きは増加
曲線の傾きが減少しだした後、曲線は水平な直線になる。
この内容から、S字型曲線の内容の中で、わかる事がある。
私が負けてしまう時は、、、この曲線の傾きよりも傾きに対しての時間軸を見落としがち が原因で負ける時がある。
しかし、1度捉えた相場では、当然連勝や高い期待値が、、、見込める相場にある。だから無駄負けがしなくなるのは事実ある。
この記事でも負けの回避方法と、勝ち方、フラクタルの見つけ方を
記事後半に記載していきます。
私のコンサル生ならわかるかもですが、私ってエントリー相場の発見が早かったり、フラクタルに対しても、、見つけ出すのが早い事を知っていると思うが、、この原理、フラクタルという根本を知っているから、、、すぐ見つけ出せたりすることができているのは経験ではなく相場の理屈(本質)と根本的な部分を知っているだけの事なので、だれもがこの根本を理解することで、フラクタルの勝率・根拠や点数付けや深く来る時と浅い時が理解できるようになる。
その内容の1つは公開します。
S字型曲線=最終的に t → ∞ で漸近する水平な直線は N = K の直線であり、時間が経過すると最終的には、個体数は環境収容力の値に収束するということである
そのことから、環境収容力の値に収束するこの理屈が探せる事が早くフラクタルに気付ける思考の理由の1つであるとわかる。
(↑相場には周期があり、周期が伸びているときには、逆張りは不向きであり、収束しているときには特にBOは向いているって事です。)
+自力で感覚を養うなら、スクショをガンガン集めていくと感覚が覚醒する。ので騙されたと思って100枚から1000枚くらいはスクショを集めてみてください!
平衡状態の安定性
ライントレードよりの話にもなるが、、このフラクタルがライントレードにも同じ現象が起きる事もある。
(※こちらも有料ページにて画像と共に解説します)
これは有料ページから参考画像にも該当してしまうのでお見せすることができないが、、根本を知るとMT4から探せると思うので、、、
記載します。
ラインでは、N = 0 および N = K のときはいくら時間が経過しても個体数 N は増加も減少もしないことから、平衡状態では、N = 0 または N = K という一点に留まり続ける。数学の力学系分野では、このような点を不動点や平衡点と呼ぶ。
その平衡状態の点から少しずれたとしても、時間が経過すれば平衡状態へ戻り、収束することを意味している。
また、不安定な平衡状態とは、平衡状態の点から少しずれたとき、時間経過すると平衡状態とのズレはどんどん大きくなっていき、平衡状態に戻らないことを意味している。(これがラインが効かなくなった相場を指す=ブレイクシーン)ライン生徒には理解できるかな??
ロジスティック方程式の場合は、N = K の時の平衡状態が安定、N = 0 時の平衡状態が不安定となっている。
すなわち、初期個体数 N0 が K または 0 であれば、時間経過によらず常に同じ値を取り続けることは同じだが、N0 が平衡状態から少しずれたときの挙動は正反対となる。(ラインに対してブレイク押し目順張りしていく事のような状態)
ここまでで訳わからん状態でお読みいただいた方はある意味正常です。笑
定義域と値域
ここで一度応用動画も視聴して振り返ってみましょう。
これまで(note全記事)の記事の内容を見返すとN値計算を含めて解説してきているのには、値幅というだけあって、もっと深くまで値動きされる事もあるでしょ?ってお考えの方も少なくないと思います。
しかし、値幅が動くにもある程度の領域があるシーンがあります。
まずはこちらをご覧ください。
こちらの内容は、縦軸と横軸の軌道の変化と可動の変化を見れます。(これがわかると・・・面白いリ〇〇スの理屈がみえます)
この短い動画の中に一定の領域になった瞬間に瞬間的に赤線が黒の斜めの線から一定の値幅観測が起きる現象が起きている事が理解できると思います。
この状態がおきているときに、値幅理論やこの後わかるが、7秒で止めると

リアクションから起きる現象から、フラクタルによる波の修正とリアクションから根拠にもなる内容が見つけ出せます。
この内容は有料ぺージにて参考動画をご視聴ください。
この内容を片隅に入れ相場と組み合わせて理解していくことで、感情的なエントリーや根拠の薄いエントリーから抜け出せるようになります。
相場のフラクタルの波
相場のフラクタルというのは1つの波が起きていて
その波が再度形成され起きる状態にいる事なのですが
これを海の波としてイメージしてください。
海は天気がいい早朝は静かで波がほぼありません。
しかし、夕方につれて(ロンドン時間)波が大きく起きてきます。
塩の満ち引きの関係ですが、この波が起きて、何かに波がぶつかり大きな波が割れた後に、小さな波が起きます。
その小さな力のない波を捉えていこうよ!
っていうのが、フラクタル+出来高+N値計算の今回の手法です。
そして今回の記事では、特典としてフラクタル+リトレースを使用した
エントリーPOINTの得点動画をお付けして、理解を深めていただこうと思います。
上記にある、11秒の動画の意味合いが理解できるようになると思います。
この後の動画を2回動画を見ると、相場を見るのが面白くなる事はお約束できます。
このトレード内容を見ていくと、、、面白い発見が自身で見つけられるほかに、たとえチャンスを逃しても、、、その後にチャンスが訪れるタイミングがわかるから・・・
無理に熱くなって追いかけるトレードしてしまったりする方には、このチャンスを逃した後の数十分後には、チャンスが来るかもしれない。
って待てる知識を入れてあります。
そしてフラクタルには、細部のフラクタルと言われている部分があります。
この細部についても理解を深めていただければもっと楽しくなってます♪
参考フラクタル画像
今回のフラクタルの捉え方については判定時刻に制限を決められている事とマッチしてバイナリーオプションとのトレード愛称で有効な手法になります。
これがfxだった場合はスキャルにはもってこいの手法です。
「フラクタルを知って相場を見るのが面白くなる」
きっかけになっていただけれたらと思います。
次回記事では大きな波も捉えていく話をしていきますので
FXでもピプスが抜ける記事更新していきます。
この相場の波というものには、一般トレーダーが参加していい波と一般トレーダーが参加してはいけない波があり、大きな波に、一般トレーダーが逆張りで抵抗しても、結果、大きな波にもみ消されます。
それは大きな時間軸の波を見ずに、短い時間軸の波ばかりを見すぎて
勘違いしてしまっているわけです。
この小さな波を大きな方々が作りあげてくれた残りの波も大きな波をもとに
形成される事は必然でもあるわけです。
事実、相場はそのように動く事がわかります。
例えばこれは今日3月25日EUR/AUDのチャートです。

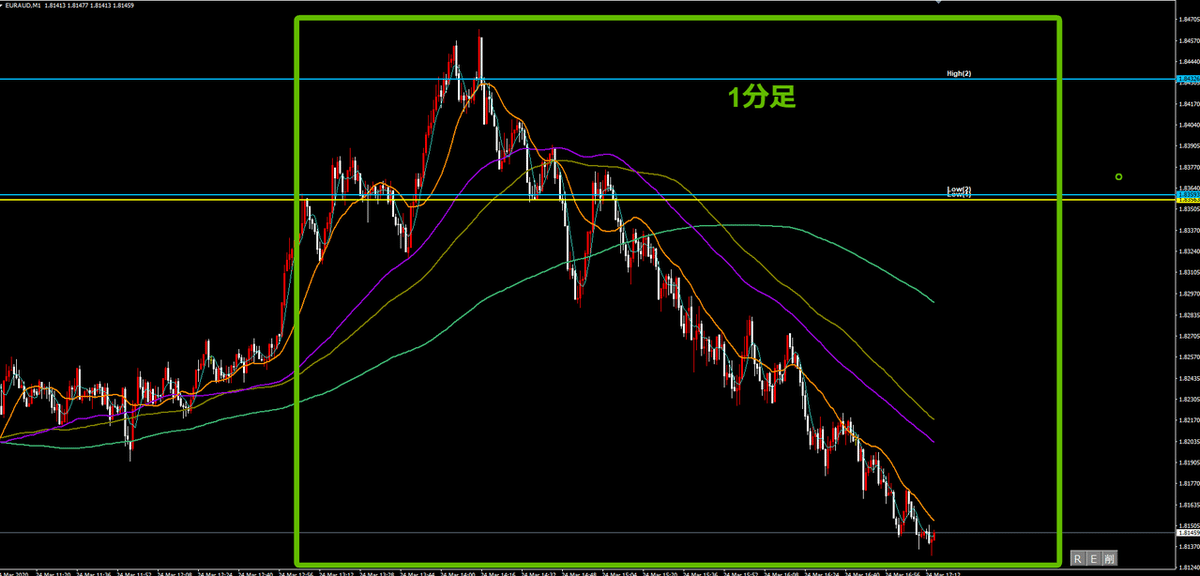
何言いたいか、、、雰囲気伝わりますか??
だからこの後の解説ではそんな上記の記事のすべてをMT4の実際のチャートを使用して理解しやすいように
動画+ライン画像+フラクタルの見つけ方+リトレース使用動画の1部についてチャートにはめ込み解説していくとします。
購入後は、20枚以上(27枚)の写真や画像で解説など(随時追加)
5800文字以上で解説(随時 追加済み)
360分以上の動画で解説(ZOOM利用して講義も追加)
になっております。
SEOの関係上の対策の為、PW付きのページリンクにて購読いただけます。
2020/10/06 最終記事更新
更新内容は記事のみならず、講義も計約10時間ほど行い、実際に購入者様も月間勝率70%をたたき出している方も出始めました。
これは、うれしい報告でもあり私自身も再現性を導きだせた事で、裁量という大きな壁を越え、手法伝達が行えました事が何よりうれしく思います。
フラクタルの見つけ方
ここから、相場からフラクタルを見つけ出せる簡単な方法をお教えしていきます。
相場とは、、、
ここから先は
¥ 9,800
宜しければサポートお願い致します。今後の励みにもなりますし、今後も情報配信していく事を喜びと感じれるトレーダーとしても1つ成長したいと思っています。
