
【最新年度を解説!】令和6年度「都立青山高校」推薦小論文 解答と解説
はじめに
本記事は、令和6年度の「都立青山高校」推薦小論文<文系・理系>を解説しています。
本記事で解説している問題は、次のリンクからご覧いただけます。
>>> こちらをクリック
ではここから、解説に入ります!
【第1問(文系パート)】
政党とは- 政治について同じような考えをもつ人々の集まり
政権獲得を目指して活動
→ 現代の政治は政党中心(政党政治)
→ 複数政党制による民主政治の実現(二大政党制,多党制など)
<解答の指針>
問題文にある次の文章を参考にしましょう。
日本の衆議院議員選挙- 小選挙区比例代表並立制
・小選挙区制:一つの選挙区から一人の代表を選ぶ。
・比例代表制:各政党の得票数に応じて議席を配分する。
★重複立候補:衆議院議員選挙では,小選挙区制と比例代表制の両方で立候補することができる。小選挙区制で落選しても、比例代表制での復活当選があり得るということ。
この問題を解くために、以下のステップで進めていきます。
小選挙区の当選者を特定する
比例代表の議席配分を計算する
各政党の比例代表当選者を決定する
ステップ1: 小選挙区の当選者を特定する
各選挙区で最多得票の候補者が当選します。
第1選挙区: A氏 (11600票)
第2選挙区: E氏 (8400票)
第3選挙区: I氏 (7600票)
第4選挙区: M氏 (12000票)
ステップ2: 比例代表の議席配分を計算する
本来の「ドント方式」は、複雑なものです。学校でも定期試験などで出題する先生もいらっしゃるので違和感を感じた受験生もいたかもしれません。本問においては、全体の時間などを考慮し作問されたのだと予想します。そこで、今回の解説でも、あくまで次の[注]として提示された説明に基づき計算をしています。
日本の比例代表制の議席の配分はドント方式に基づく。ドント方式とは、政党別得票数を1,2,3という整数で割っていき,その商の値の大きい順に定数まで議席を配分する方法である。
① 各政党の得票数を1, 2, 3で割る
<計算結果>
はる党:21000, 10500, 7000
なつ党:30000, 15000, 10000
あき党:42000, 21000, 14000
ふゆ党:27000, 13500, 9000
② 得られた商を大きい順に、上位6つの数値を探す
はる党:21000, 10500, 7000
なつ党:30000, 15000, 10000
あき党:42000, 21000, 14000
ふゆ党:27000, 13500, 9000
③ ②から政党に議席を配分する
<議席配分>
あき党:2議席
なつ党:2議席
ふゆ党:1議席
はる党:1議席
ステップ3: 各政党の比例代表当選者を決定する
小選挙区での当選者を除外し、同順位の場合は惜敗率の高い方を優先します。惜敗率は計算する必要はなく、表に記載されています。
はる党 (1議席)
F氏 (惜敗率96%) と N氏(惜敗率88%) が同順位→ F氏
なつ党 (2議席)
W氏(E氏, I氏は小選挙区での当選者のため[注]より除外)
B氏 (惜敗率81%) と P氏(惜敗率57%) が同順位→ B氏
あき党 (2議席)
Q氏(A氏は小選挙区での当選者のため[注]より除外)
G氏 (惜敗率67%) と L氏(惜敗率26 %) が同順位→ G氏
ふゆ党 (1議席)
O氏 (惜敗率79%) とH氏(惜敗率33 %)→ O氏
したがって、政党別候補者名は以下のようになります。
はる党:F氏
なつ党:B氏、E氏、I氏、W氏
あき党:A氏、G氏、M氏、Q氏
ふゆ党:O氏
問2
<問題分析>
・現在の衆議院議員選挙が「小選挙区制と比例代表制を並立させている」理由について、青山さんのノートを参考に述べなさい。
・小選挙区制と比例代表制のそれぞれの短所に触れて記述すること。
・文字数は300字程度とする。
<解答の指針>
記述・論述の場合「文字数」は大きな要素です。300字は長いように思えますが、必要な条件を満たそうとするとそこまで長くはありません。
まず、明確に指示が出ている「小選挙区制と比例代表制のそれぞれの短所」を整理しましょう。コツとしては、メリットとデメリットをセットで考えると言語化しやすいです。
問2 現在の衆議院議員選挙が小選挙区制と比例代表制を並立させている理由について, 青山さんのノートを参考に述べなさい。その際,小選挙区制と比例代表制のそれぞれ の短所に触れて記述すること。ただし,文字数は300 字程度とする。
解答をする際の素材
問題文の指示では「青山さんのノート」とありますが、
・中学校の授業で習った内容
・時事問題に関する知識
・問1で得られた計算結果
を活用して解答する必要があります。
・現代の政治は複数政党制により、民主政治を実現する
・小選挙区制は一つの選挙区から一人の代表を選ぶため(選挙結果が明確になりやすく、政権の安定を図ることができます。しかし、一方で)少数派の意見が反映されにくく、少数政党の議席獲得が困難になる、得票率が議席数に反映されないことがあるという問題があります。政党間の議席獲得数が得票率に比例しない場合も生じ、必ずしも民意を反映した結果とならない可能性がある。
・比例代表制は政党ごとの得票数に応じて議席を配分するため(少数派の意見も反映されやすく、民意を幅広く反映することが可能です。しかし)比例代表制は政党数が多くなると、政権が不安定になる可能性が高くなります。比例代表制では、候補者と有権者の結びつきが弱くなり、政党の影響力が強まる傾向がある。また、小政党が乱立し、政局が不安定になる可能性も孕んでいる。
・小選挙区制の「安定性」と比例代表制の「民意の多様な反映」の両方を実現するために、現在の衆議院議員選挙ではこの2つの制度が並立されています。
・現在の衆議院議員選挙が小選挙区制と比例代表制を並立させている理由は、それぞれの制度の短所を補完し合うためです。
そこで、小選挙区制と比例代表制を組み合わせることで、それぞれの短所を補い合い、
多様な民意を反映できる選挙制度を目指している。小選挙区制によって地域代表を選出しつつ、比例代表制によって政党の得票率を反映させることで、よりバランスの取れた政治を実現しようとしていると言える。
これら二つの制度を並立させることで、民意の反映と政権の安定性のバランスを取り、より民主的な政治の実現を目指しています。また、重複立候補により、小選挙区で落選しても比例代表で復活当選の可能性があり、多様な人材の確保にも寄与しています。
[解答]
小選挙区制は、選挙区で最多得票を得た候補者だけが当選するため、民意が必ずしも議席数に反映されない。また、少数政党は議席を獲得しにくく、多様な意見が反映されにくいという問題がある。
一方、比例代表制では、政党の得票率に応じて議席が配分されるため、小政党も議席を獲得しやすく、多様な意見が反映されやすい。しかし、政党間の交渉が複雑化し、政権が不安定になりやすいという欠点がある。
現代の政治は複数政党制により、民主政治を実現する。そのため、小選挙区制と比例代表制を並立させることで、それぞれの制度の短所を補完し合い、より良い選挙制度を実現させるためである。
小選挙区制と比例代表制を並立させることが「それぞれの制度の短所を補完し合う」ことになる理由を説明します。
小選挙区制の短所(民意の歪み、多様性の欠如)を比例代表制が補完する:
小選挙区制では、1つの選挙区で1人しか当選しないため、2位以下の候補者に投票した人々の票は議席に反映されません。これは、民意を歪める可能性があります。
比例代表制では、政党の得票率に応じて議席が配分されるため、小選挙区制で議席を獲得できなかった少数派の意見も国政に反映することができます。
小選挙区制では、地域ごとの有力候補や政党が有利になりやすく、多様な意見を持つ候補者や政党が当選しにくい傾向があります。
比例代表制では、全国規模で政党への投票が行われるため、特定の地域に偏ることなく、多様な意見を持つ候補者や政党が議席を獲得する可能性が高まります。
比例代表制の短所(政局の不安定化、候補者と有権者の繋がりの希薄化)を小選挙区制が補完する:
比例代表制では、多くの小政党が議席を獲得する可能性があり、連立政権が成立しやすくなります。しかし、連立政権は政局が不安定になりやすいという側面があります。
小選挙区制では、1つの選挙区から1人の代表が選ばれるため、政権担当能力のある政党が過半数を獲得しやすく、安定した政権運営につながりやすくなります。
比例代表制では、有権者は政党に投票するため、個々の候補者との繋がりが希薄になりがちです。
小選挙区制では、候補者は選挙区内の有権者と直接触れ合い、地域の声を聞く機会が増えるため、候補者と有権者の距離が縮まり、地域代表としての責任感が強まります。
このように、小選挙区制と比例代表制は、それぞれの短所を補い合い、よりバランスの取れた選挙制度となるように機能しています。
例えるなら:
小選挙区制と比例代表制の関係は、**「短距離走が得意だが長距離走が苦手な人」と「長距離走が得意だが短距離走が苦手な人」**がチームを組んで、短距離走と長距離走の両方がある駅伝レースに出場するようなものです。それぞれの得意分野を生かし、不得意分野を補い合うことで、チーム全体として良い成績を残せる可能性が高まります。
同様に、小選挙区制と比例代表制を組み合わせることで、それぞれの制度の弱点を克服し、より良い選挙制度を実現することが期待されています。
第2問(理系パート)
理系パートをお読みになる際のお断り(前提)
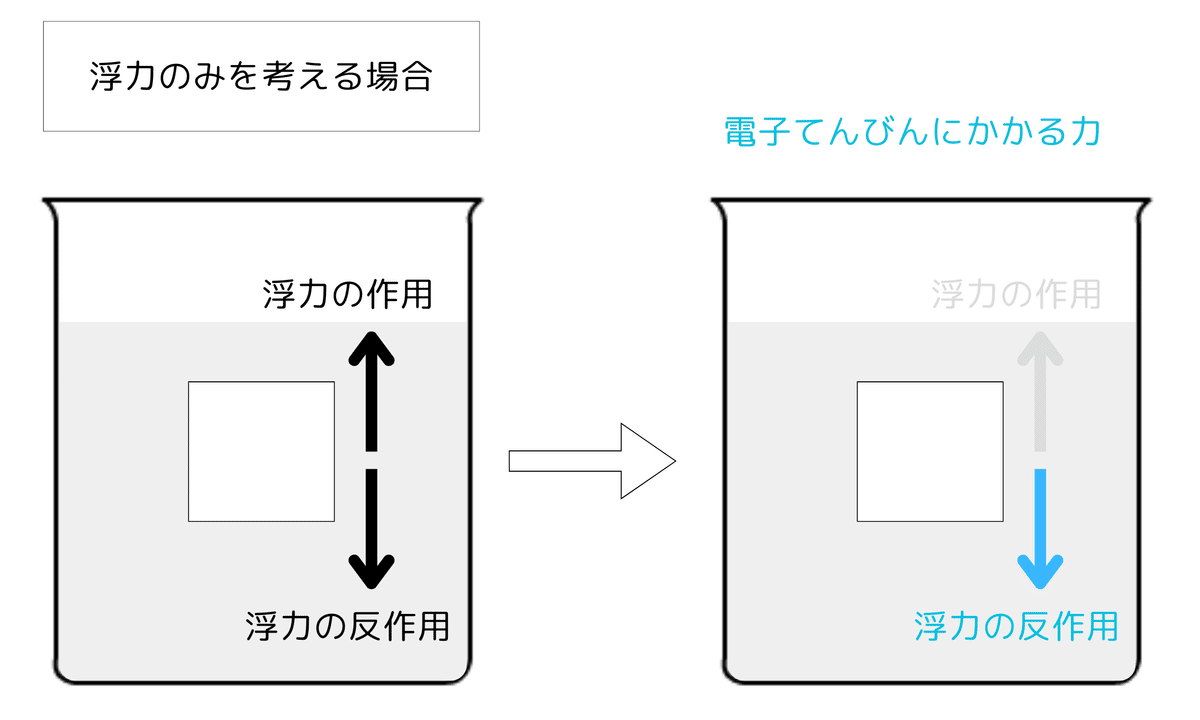
浮力を考える場合、次の3つの場合を考えます。
① 物体の一部が水面より上に出ている
② 物体が水中にある(物体はビーカーの底に触れていない)
③ 物体がビーカーの底に触れている
今回は②のケースでとなります。重要な点は「電子てんびん」による測定に影響を与える力(重さ)です。「浮力」は高校でしっかりと習う重要単元ですが、本問の場合は次の点を理解しておく必要があります。
・「浮力」は物質の水中にある部分だけを考えます
・「浮力」の大きさは、水中にある体積×水の密度
・「浮力」は作用・反作用の考え方を用います
厳密に計算する場合は、水でも温度によって密度が異なるため注意が必要です。
ここまでが、本問を扱うための前提となります。
【理系】解答・解説パート
問1の解答・解説
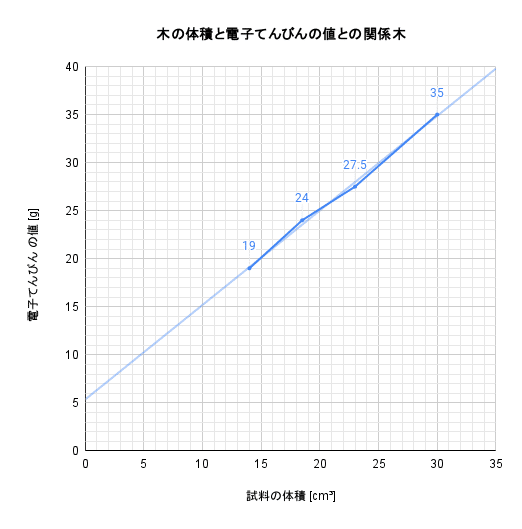
問1 <結果1>の空欄に入る数値を試料の質量と密度から求め,試料の体積と電子てんびんの値との関係を示すグラフで表しなさい。グラフのデータの点は明確に示し,データの点を適切な線で結ぶこと(直線のグラフなら定規を使用し,曲線のグラフならフリーハンドで書くこと)。

「浮力」に関しては、中学受験の経験の有無や、学校や塾の先生次第で理解度に差があります。ただ、上記のようなヒントが与えられている場合は、確実に計算をし、完璧なグラフを作成したいところです。
空欄「試料の体積」は、「試料の質量」を「試料の密度」で割って求めることができます。なお、割り切れない場合は、小数第2位を四捨五入して値を求めましょう。(有効数字は数学や理科の教科書を参考のこと)
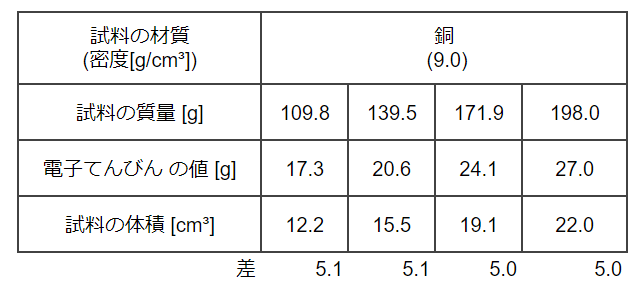


上記の「差」は、「電子てんびんの値 [g]」と「試料の体積[cm³]」です。これが何を意味するのかは後ほど説明しますが、本来は単位が異なるため足し算・引き算をすることができません(後ほど説明します)。
上記の表ができたら、グラフを作成していきます。今回は、紙面の都合上、次のような形式で作成をしました。試験では凡例(はんれい)にならった記号を使うようにしてください。


問2の解答・解説
問2 問1のグラフはいずれも、原点を通る直線にはならなかった。その理由を説明しなさい。
さて、3つのグラフを作成して気づいたでしょうか?今回は、縦軸も横軸も同じものが使われています。この3枚を重ねると次のようになります。

実験データのため、多少の誤差がありますが、(高校受験レベルですので)これは「同じ直線」と言っても問題ありません。
ということは「試料の種類」による違いはないということになります。本問では「試料の種類」の違いは、「密度」の違いということになります。
「浮力」がチンプンカンプン(=よく分かっていない)でも、ここまでは解答しておきたいところです。
このグラフは何を意味するのか?
本問で与えられた表にある「電子てんびんの値」は何を表しているのでしょうか。実験の操作をしっかりと読むと「ビーカーと水の重さ」は無視することができます。


この「力」は物理のという単元に含まれます。中学校での扱い方(最近では高校での扱い方)も大きくばらつきがあるため、迷いましたが次のように種類を分けて説明をしました。


このように力の大きさは等しいので、打ち消し合うことになります。そのため、電子てんびんの値には影響しません。よって、この浮力(反作用)の力(重さ)だけが電子てんびんの値に影響をします。

<補足> 質量と重さは何が違うのか?
これは上皿てんびんやばねばかりなどを用いて説明されることが多いです。学校の教科書や試料集にも説明がありますので、確認をしてください。(この説明は、本記事の主旨からズレてしまうので割愛)
なお、F(力)=m(質量)× g(重力加速度)という物理のルールがあります。g は定数として考えるため、中学の範囲では「質量」と「重さ」をごちゃまぜに考えても問題ないことが多いです(本当は問題です…)。一方で、上記の式から「重さ」=「力」が成り立つことは知ってほしい点です。

よって、この表を例にとれば、電子てんびんの値=(生じた)浮力の大きさ、と考えることができます。では、この理解のもとに問2に進みます。
<POINT>「差」で生じる約5.0の数値の正体は何か?
電子てんびんの値は、ビーカー(水中)内で生じた浮力の大きさです。ここで、アルキメデスの原理を振り返ると、浮力の大きさは押しのけた水の体積に関係していることが分かります。
<補足> 水は 1㎤ で 1g とは限らない
水は常に 1㎤ で 1g ではありません。気圧(圧力)や気温(温度)により、その密度は変化しています。「そんな細かいことを考えるの?」と思われる方もいらっしゃるかもしれません。しかし、細かいことではなく、中学受験の問題のテーマとして扱われる有名テーマです。 本問においては 1㎤ で 1g として説明をしますが、問題内ではこの点はあえて触れられていません。問題が複雑化するためだと思われます。

本問では、試料は完全に水の中に入っており、それが受ける浮力の大きさは、体積×1[g/㎤] で求めることができます。すると、例えば上記の場合は、試料の質力が109.8g の場合、試料の体積が12.2 ㎤となるわけですから、受ける浮力は、12.2 [㎤]×1[g/㎤] =12.2[g] となるはずです。しかし、電子てんびんの値(=観測される浮力の大きさ)は、17.3g となり約5gの差が生じます。これは、試料の質量を変えても、同じ差が生じることが上の表から確認できます。
電子てんびんの値=浮力の大きさ、という事実は変わりません。となれば、試料以外に対して浮力が生じていると考えることができます。
そこで、再度、図を確認すると、水中の中には試料以外の物体もあります。これらは、スタンドに固定されているため、その重さは電子てんびんの値に影響しません。しかし、水中にある以上、浮力が生じます。

今回の表では、棒や金網の体積や質量に関する言及はありません。しかし、問題文に「ただし、棒や金網の体積は考えないものとする」などの条件が記載されていないのであれば、考える対象となります。
棒や金網の質量については、スタンドに固定されるため考える必要はありません。よって、水中にある部分の体積が本問で問われてる部分となります。
各表で出てくる「差」に該当する 約5.0g は、この棒と金網に対する浮力の大きさで、その体積は 5㎤ と考えることができます。解答用紙の大きさを考慮すると、次のような解答が考えられます。
水中には試料以外にも、金網と棒の一部があり、それに対して浮力が生じているから。
問題3の解答・解説

浮力は水中にある物体に対して生じます。上記の図から分かるように、傾けることで、水中にある部分の体積が大きくなります。よって、状態Bのとき、生じる浮力が大きくなります。
状態Aと状態Cは対照実験です。浮力は、押しのけた水の体積の大きさで決まるため、物質自体の密度は影響しません。
以上から、状態A=状態C<状態B と分かります。
実験1からは、試料の密度によって浮力は変化しないことが分かりました。試料2からは、水中にある物体の体積の大きさが浮力に影響することが分かりました。
実験1と2から、物体が水から受ける力は、その物体の密度によらず、物体の水の中にある部分の体積の大きさによって決まることが分かる。また、水の中にある物体の体積が大きいほど、水から受ける力が大きいことが分かる。
本来、考察はあらたな仮説などを書くこともできますが、今回は試験という性質上、最小限に留めました。一般試験と異なり、厳密な採点基準を作りづらい構成のため、上記のことが書かれていれば、合格ラインの点数が与えられると考えます。
<補足> 結果ありきで問題を解いていないか?
本問の解説でお気づきの受験生もいらっしゃると思いますが、今回の解き方は純粋に「実験結果から考察を得る」というプロセスではありません。原理主義的な人は、「こんな受験テクニック的なものはよいのか」と疑問に思われるかもしれませんが、私はよいと思っています。
そもそも、純粋に科学的に取り組むなら、実験データが少なすぎる上に、前提条件の設定などやや強引です。つまり出題する方も、「建前としては実験問題だけど、実際は…」と思って出題しています。
その上で、問題の中で得られた情報のみで解答を作成することが求められているのです。
以上、令和6年度の小論文(理系)の解説をお届けしました。
↓↓↓↓↓↓

都立青山高校のHPには、推薦入試小論文の過去問が、9年度分公開されています。
そのうち、
・平成29年度
・令和2年度
・令3年度
・令和4年度
・令和5年度
の解説を作成しました。
令和6年度と同じく、ご自宅でも塾で授業を受けたような復習がしたいというリクエストにお応えして、作成しました!
[特長]
● 都立青山高校推薦入試の小論文5年分(平成29年度・令和2年度~令和5年度)の解答例・解説を収録
● 受験指導のプロが作成した信頼性の高い内容
● 理系・文系両方の問題に対応
[どんな教材?]
・「解答解説がなく、何を使って対策したら良いかわからない...」がこれ一冊で解決します!
・都立青山高校の推薦入試小論文5年分の【解答の指針】・【解答例】がまとまった教材です。
・受験指導のプロが書いた指針・実際の答案がどのように添削されているか、どのようなレベルの解答を書きあげれば良いのかがわかります。
【販売形式のご案内】


