キツネとウサギの相互関係

感動しました！これを見て（ブラウザバックしないでくださいね。笑）

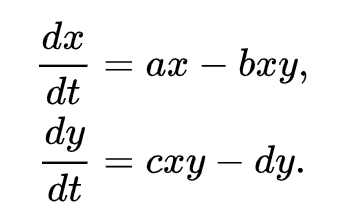
なんじゃこりゃって感じですかね？
こちら、Lotka-Volterra equations（ロトカ・ヴォルテラの方程式）と呼ばれるものです。

今日私は、これを見て感動したのです。
これは、大学の授業でfortranのプログラミングの授業を受けており、練習問題として与えられた連立微分方程式です。

実はこの数式、捕食-非捕食関係のの個体数の増減の関係を表しているのです！
仮に捕食者をキツネ（上の式では y = キツネの個体数）

非捕食者をウサギとします。（上の式では、x = ウサギの個体数）

そうするとウサギとキツネが一定数ずついたとして時間の変化と個体数の変化をシュミレーションできるのです。（私はまだ計算していないです。笑）

凄くないですか！？
まだ、よくわからないかもしれないので、もう少し説明しますね！

まずウサギの個体数。

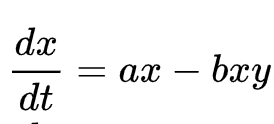
こちらですね。
この式で仮に、キツネがいなかったとします。（y = 0）
すると

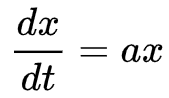
こちらになりますね。
この時ウサギの数は時間 t に対して、指数関数 x = exp(at) で増加することになります。（積分定数が出ます。）
まあ、ざっくり言うとある正の実数 a  の割合とウサギの元の個体数に関係して増えていくと言うことです！
そりゃそうですよね、キツネがいなければ補食されないのでウサギは増えますし、ウサギが5匹しかいないよりも500匹いた方が1年後にはより多く増えていそうですよね。

そしてキツネがいるときです。
このとき、

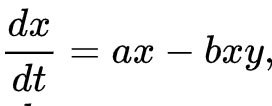
ｂｘｙでウサギが減るというのです。
ある正の実数ｂの割合とウサギの数（ｘ）とキツネの数（y）の関係式です。
どういうことかと言うと、ウサギもキツネもたくさんいた方がお互いにたくさん遭遇するよね。たくさん遭遇するということはよりたくさんウサギは食われるよねということです。

よってウサギの個体数の増減は

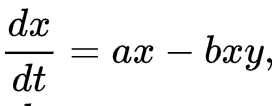
で表されるのです。
キツネも同じようにして考えれます。
詳しく見たい方はこちら（wikipedia）

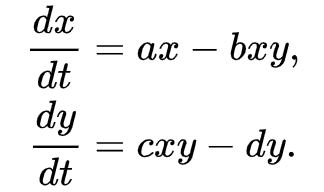
凄くないですか？
こんなシンプルな数式でキツネとウサギの個体数が5年後、10年後、どうなっていくか考えられるのです。
もちろん本当は寿命や病気、怪我、自然災害等も加味しなくてはいけないのかも知れませんが。

これを見てすごく感動しました！
そしてこれをいじれば、今のコロナの変動や、その他のこと、なんなら集団におけるカップルの増減とかも考えられるかもしれないなと思います。笑
分野的には数理生態学とからしいです。
ちょっと今後ちゃんと調べてみたいと思います！

また、今日の私の説明はテキトーな箇所や間違い等もあるかもしれません。ご容赦ください。
またしっかりと理解を深めて書くかも知れないです。

では、今日はこんなところで！
読んでいただきありがとうございました！！