μTransfer: 小規模モデルでのハイパラ探索を大規模モデルに転移し学習を効率化する
最近、友人から大規模モデルの学習を劇的に効率化しそうな下記の事実(μTransfer)を教えてもらい、こんなことが成り立つことに非常に驚くとともに、それを知らなかったことにちょっとしたショックを受けました。
μTransfer
下記の手順で大規模モデル(Neural Networks)の最適なハイパーパラメータを効率的に獲得できる
1. 学習したい大規模モデル(ターゲットモデル)と同じアーキテクチャの次元や層数のより小さいモデルを用意し、それぞれのモデルのパラメータと最適化アルゴリズムを μP と呼ばれる方法でパラメータ付けする
2. その小さいモデルで、最適なハイパーパラメータ(学習率など)を探索する
3. ターゲットモデルに小さいモデルで獲得されたハイパーパラメータを適用する
Tuning Large Neural Networks via Zero-Shot Hyperparameter Transfer", NeurIPS 2022
ここで出てくる μP(Maximal Update Parametrization)というのは、 Tensor Programs (TP)というフレームワークにおいて理論的に導出されたパラメータ付け(パラメータのスケーリングなど)の方法です。
TP は、 Neural Networks (NN)の解析をするために、線形変換や非線形活性化関数などの NN の構築で頻出する操作をリストアップし、その枠組みで成立する事象や性質を追求するフレームワークです。
驚くことに、μP はよくありがちな理論的には正しいが実装が事実上不可能な代物ではなく、後述するように実装も拍子抜けするほどシンプルです。なんならそれを簡単に適用する Python パッケージすらあります。
しかし、μP とそれがもたらす μTransfer という事実の重要さ(重大と言ってもいいと思います)にも関わらず、日本で LLM やVision/Multimodal LLM などの大規模モデルの学習に興味をもっている個人/組織の一部にしか知られていないように思われます。これが誤認であれば安心なのですが、残念ながらどうやら海外でも一部にしか正しく認知されていないようです。
このような状況になっているのは、この理論が一連の論文(現段階で Tensor Programs I 〜 VI)で段階的に構築されている途上であり、いずれも前の論文の理解を前提に書かれているのでキャッチアップするのに一定のエネルギーが必要なこと、そしてキャッチアップした人がこの理論をあまり解説していないことが一因のように思われます。それにより、この理論のフォロワーがとくに実務家のなかで増えていないようです。実際、著者の Website でも、Tensor Programs に関する入門編的な論文の一つに下記の注釈がつけられています。
"A very accessible and pedagogical intro to the scaling (with width) of feature learning. Since the TP series has a reputation for being hard-to-read, this one is not numbered so people will be more likely to read it ;)"
翻訳:
特徴量学習のスケーリング(幅)について、非常にわかりやすく教育的な入門。TPシリーズは読みにくいという評判があるが、この本にはナンバリングがされていないので、もっと広く読まれるだろう😉
上記の注釈がついた "A Spectral Condition for Feature Learning" という論文(後で紹介します)もたしかに理論に関しては「非常にわかりやすく教育的」ではありますが、この論文では μTransfer は言及されていません。先に出ているはずの Tensor Programs V の論文で μTransfer が発表されているのですが、逆にこの論文だとあちこちを参照しないと理論背景を理解するのが難しいのが実情で、理論と効果を両方理解するには両方の論文を読む必要があります。
また、いくら実装がシンプルと言えども理論の理解なしでは正しく使うのは困難です。とくに大規模モデルであるほど気軽に試行錯誤はできないでしょう。実は μT を簡単に使えるようにするために開発された著者による Python パッケージもあるのですが、こちらはこちらでコメントがほぼ付いていなかったり例が簡単すぎたりして、理論の輪郭を知らないともう少し複雑なモデルに対してどう適用すればよいかには不安が残るでしょう(ただし、実装自体は非常にコンパクトなので理解の答え合わせにはとても便利です)。
というわけで、初学者向けに理論の輪郭を描きつつ、どう利用すればよいかの指針を与えることが必要なのではと思い、自分で多少キャッチアップして記事にしてみました。これをきっかけにさらなる解説記事や適用例が増えることを祈っています。そして、すでに TP / μP / μTransfer に関して理論的にも実践的にも熟知されている方がいたら、ぜひ追加の解説記事など作っていただけるとありがたいです。
なお、このような経緯で書いたものなので、私自身、この理論に関してはまだまだ初心者です。誤りや不適切な表現があればご指摘などいただけるとありがたいです。
※ なお、μTransfer に関しては少なくとも 2021 年の中頃までには、Microsoft と OpenAI には周知であったようです。というのも、後述の Tensor Progmram V と同内容の論文が NeurIPS 2021 に投稿されており、その著者群が Microsoft と OpenAI の連合軍なので。また、GPT-4 の Technical Report にも引用無しで Tensor Programs V の論文がさらっと reference に入れられており、GPT-4 の開発時も μTransfer 等により効率的にハイパーパラメータ探索がなされていたのではと推測しています。
本記事を読むことの効用
(知らなかった読者にとって)大規模モデルの学習をおそらく圧倒的に効率化できる汎用的かつシンプルなパラメータ付け μP の存在と使い方を知ることができる。
Neural Networks に対してかなり一貫性のある理解が得られそうな気分になる。学習率やパラメータの初期化のスケールに関する話がなんでも TP/μP で取り扱うべき事項に見えてくる。
本記事には書いていないこと
「Feature Learning」とは何か。何ができるのか。
NN の無限次元極限での振る舞いと有限次元での挙動との関係性。
NTK や GP としての Neural Network の解釈との関連性/差異。
Python パッケージ mup の使い方。
証明の細部など。
μTransfer -- サイズの異なるモデル間のハイパーパラメータ転移
まずは何ができたのかをもっと具体的に知ってもらうために、下記の論文で示されている結果を紹介します。NeurIPS 2021 にも同内容の論文が投稿されているのですが、著者のサイトに従い、2022 年の arXiv version を紹介します。
μTransfer は、μP (Maximal Update Parametrization)という理論的に導出された NN のパラメータ付けにより実現される、サイズの異なる NN 間のハイパーパラメータ転移です。
下記の表で μTransferable に分類された(ハイパー)パラメータを μP に従いパラメータ付けしておき小さいモデルなどで最適値を探索しておくと、μTranferred Across に分類された(ハイパー)パラメータを変えたモデルへそのまま転移してもほぼ最適に動作するようになります。しかも、この事実はモデルのアーキテクチャ(MLP、ResNet、BERT、GPTなど)によらず、同じアーキテクチャ内では一般的に成立します。

より具体的には、下記のようなことが可能になります。
μP を使うとモデルの次元数を変えても同じ学習率を使い回せる
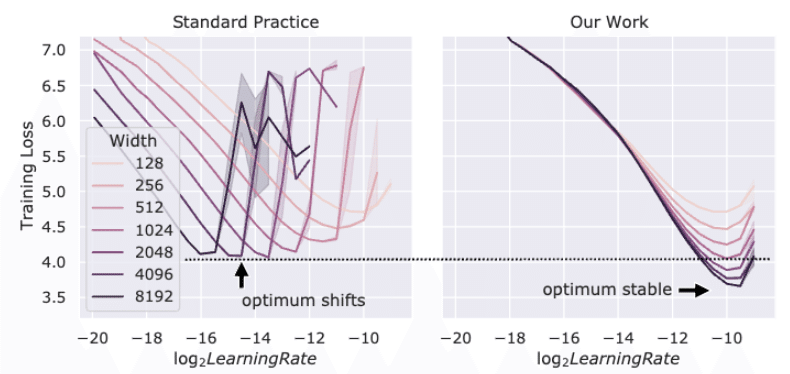
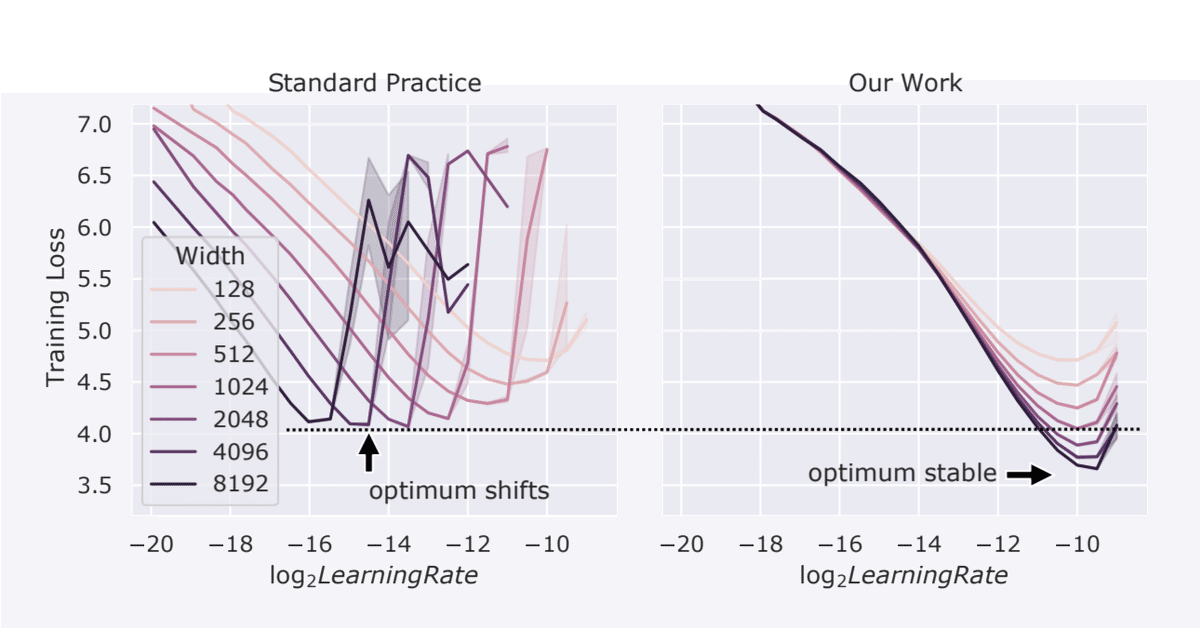
上のグラフのとおりなのですが、パラメータの初期化などを PyTorch などで実装されている kaiming uniform などの標準的な方法(Standard Practice、SP)で行った場合、モデルのサイズ(上図ではネットワークの width=次元数)を変化させると当然ながら最適な学習率は変化します(グラフ左)。
一方、μP に基づいてパラメータ付けをした場合、驚くべきことにサイズを変えても最適な学習率に対する精度に明らかな一致性が見て取れます。しかも、モデルサイズが大きいときは SP の精度を顕著に上回ってさえいます。
したがって、μP にもとづいたパラメータ付けのもとでは、width の小さいモデルで学習率をチューニングしておけば、その学習率を任意に大きなモデルにそのまま使い回せることになり、時間・金額の大幅な削減に繋がります。
学習率以外も同様に転移可能

上図では、Transformer ベースのネットワークの場合に、学習率の他、 weight のスケーリングパラメータ、weight の初期化時の標準偏差の大きさ、学習率のスケジューリングに関してもやはりモデルサイズ(width = 次元、depth = 層数)を変えても転移することが示されています(ただし、weight 初期化時の標準偏差に関しては depth にたいする転移はできていませんが、詳しくは論文を参照してください)。
μP に従ったパラメータ付けの実現方法
では、どのようにしてこのような驚くべきハイパーパラメータ転移を実現しているのでしょうか?実は非常にシンプルな方法で実現できるのです。
下記は、Tensor Programs V の論文に記載されている実現方法をあらわす表です。表中の fan_in、fan_out は PyTorch の Linear のデフォルトの初期化方法である kaiming_uniform_ などでも使われるfan_in、fan_out と同様で、入力次元数、出力次元数を表します(Convolution だと receptive field を考慮する必要がありますが事情は同様です)。

(驚いてばかりですが)驚くべきことに実は上記の表の黒字と赤字(purple)のスケールで weight の variance、optimizer の学習率のスケールを取るだけで μTransfer は実現されます。このパラメータ付け(スケーリング)が μP です。たとえば、SGD を使う場合はモデルサイズの変化に従って下記のようにスケールさせ、それ以外は通常と同様に学習すればよいことになります。
パラメータの初期化
出力層以外の weight とすべての bias → 分散 1 / fan_in でスケーリング
出力層の weight → 分散を 1 / fan_in^2 でスケーリング
学習率
入力層の weight とすべての bias → fan_out でスケーリング
出力層の weight → 1 / fan_in でスケーリング
中間層の weight → スケーリングなし
なお、この表と mup パッケージの実装を比べると若干の差分があり、出力層の初期化は mup パッケージではゼロ初期化が採用されています。したがって結果的に出力層の初期化時のスケーリングは不要になります。これについては下記の Issue で説明がされています。
この Issue によると、μP に従った場合、出力層の width (次元)が大きくなると漸近的に Gaussian Process に近づくのですが、その分散が 1 / width のオーダーになります。width が小さいセッティングと width が大きいセッティングでは学習の軌跡が大きく変わるらしく、ゼロ初期化であればこの差が生じにくいのでゼロ初期化をしているとのことです。ゼロ初期化をした場合、結果的に先の表で特別扱いされていた出力層のスケールは無視して良くなり、全パラメータを 1 / fan_in でスケーリングすれば良いことになります(依然として学習率は調整が必要です)。
mup パッケージの実装は非常にシンプルで、MLP、ResNet、Tranformer での example がついているので、実装の詳細を確認したい読者は example を参照してみてください。
以下では、なぜこれでうまくいくのかの理論的な枠組みを説明し、μP の道具としての使い方を理解していこうと思います。
なぜこれでうまくいくのか -- 学習中に特徴ベクターのスケールを width によらない一定スケールに保つ
μP で何をしたいのかについては、下記の論文が見通しが良いです。Tensor Programs I 〜 V の構築途上において何種類かの理屈の説明がされているようですが、自分としてはこの論文が一番平易でわかりやすかったです。
Greg Yang+, "A Spectral Condition for Feature Learning", 2023
以下、話を簡単にするため、バイアス項なしの Multi Layer Perceptron (MLP) をイメージしながら読んでください。実現したいこと/できることは他のネットワークアーキテクチャでも同様です。
まず、μP では、モデルのサイズによらないスケールをもつ特徴量(中間層のベクターの各次元のことを特徴量と呼ぶことにします)の獲得を目指します。l 層目の特徴ベクターを h_l (次元数 n_l)として、具体的には下記の成立を目指します(Feature Learning という思わせぶりな名前がついており、その背景は非常に面白いのですが割愛します)。
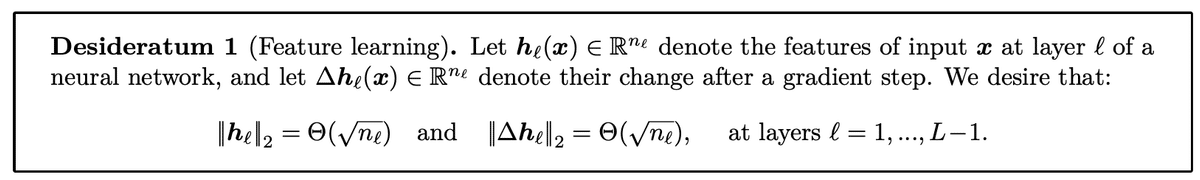
これは h_l のいずれの次元の値(特徴量)もその更新量も Θ(1) であること、すなわち、モデルのサイズに依存しないことを意味します。これにより、特徴量は学習の間を通して、モデルのサイズに依存しないスケールで変動し続けます(学習ステップ数のスケールは無視しています)。その意味で、これを満たそうとする μP は初期化だけではなく学習のプロセス全体において、特徴量のスケールを一定に保ちながら学習する方法となります。
μP ではこの要請に加えて、更新量がある意味で最大(学習効率が最大)になることを要請します。これが μP のμ(maximal update)の部分なのですが、本記事では maximal update の詳細を説明するよりも、何をどうするとどういう恩恵があるのかの仕組みの説明を行いたいので maximal update の説明は行いません。興味のある方は下記の論文などを参照してください。
Greg Yang+, "Feature Learning in Infinite-Width Neural Networks", 2020
さて、先の要請を実現するには安直には以下のプログラムに従えばよいはずです。
要請を満たすようにパラメータ(W)を初期化する
要請を崩さないようにパラメータ(W)を更新する
これは具体的には下記の条件を満たすことで実現されます。

ここで行列のノルムはスペクトルノルム(以下ノルム)です。”A Spectral …" の論文では、適当な仮定(次元が非減少 n_{l-1} <= n_l など)のもと、この Condition 1 により先程の要請が高確率で満たされることが示されています。
では、この Condition 1 は具体的にはどうやって満たせばよいのでしょうか?
実はそれを実現するのが μP です。再び安直に考えると、
W_l のノルムが sqrt(n_l / n_{l-1}) のスケールになるように初期化する
ΔW_l のノルムが同じスケールになるように更新する
の両者を満たせばよさそうに思えます。実は適当な仮定のもとでこれは正しいことが示されます。こうして μP の実現方法が得られました。つまり、上記の通りのスケールで Weight W_l を初期化し、同様に ΔW_l が同じスケールになるように学習率を(アルゴリズム毎に)コントロールすれば良いのです。
※ bias について言及しなかったですが、類似の考え方で扱えます。詳しくは、"A Spectral …" の論文を参照してください。
※※ 学習率を転移すると言いながら学習率をスケーリングするとはどういうことかと思われる方がいるかもしれませんが、学習率のサイズに依存しないようにパラメータ付けし、そのパラメータ付けにおける最適値を転移します。
初期化はアルゴリズムによらずに行えますが、学習率はアルゴリズム事に導出する必要があります。それを SGD と Adam について具体化したのが先ほどのせた下記の表というわけでした。

まとめ
以下のことを説明しました。
特徴ベクターとその更新量のスケールが次元毎にモデルサイズに依存しないスケールになるようにする Feature Learning
Weight や学習率のスケールを μP に従ったスケールで取ることで、Feature Learning が実現されることが示される
その場合、モデルサイズによらず学習率などのハイパーパラメータを転移可能になる
しかし、Feature Learning と呼ばれている由縁やそれが何を実現しようとしているのかなどについては説明していません。興味のある方は他の Greg Yang の論文を参照してください(そして解説記事などを作っていただけるとありがたいです)。
さいごに
証明の細部はすっ飛ばして(というか自分に詳細を正しく簡単に伝える力がないので)概要を説明してみたのですが、なんとなく輪郭がつかめたでしょうか。ごく自然な要請から導かれたパラメータ付けで魔法のような効果が得られ、Neural Networks の本質を垣間見た気がしました。
興味を持たれた方のために、Greg Yang らによるブログ記事を置いておきます。いずれもとても印象的です。さらに詳しく知りたい方は Greg Yang のホームページにある論文を参照してください。
最後に、宣伝です。私が代表を務める合同会社 nouu(ノウ)では、AI やデータ活用のアドバイスや技術/組織立ち上げ支援、研究を行っています。お仕事の相談を含めご興味を持たれた方は気軽にご連絡ください。雑談でも結構です。
