見出し画像

行列の積に親しむ

TataTap

はじめに

　この記事は日曜数学 Advent Calendar 2024 12月20日(金)  の記事です。(https://adventar.org/calendars/9972)
 　Xに上げたタイムラスプ動画とともにお楽しみください。

　「日曜数学」に合った私の趣向のひとつとして、数学の体系の再構築というものがあります。
　計算用紙を用意して、何も見ずに、簡単なテーマや命題を決めて、概念の定義など道具立てをひととおり揃えて目標とするテーマや命題の証明を完結させるのです。

　本日(2024年12月20日)は、この再構成をお見せする手段として、タイムラスプ動画を使ってはどうか、というアイディアを形にしてみました。
　とはいえ、やみくもに計算用紙を埋めていく様子を見せるのも極端ですので、行列の積を計算としてではなく論理的な道具として使う、という切り口で線型代数の基本的な話題と、幾何、代数からシンプルな話題を用意しました。
　趣味や研究の成果という意味では異色ではありますが、みなさんの個人的な数学活動の幅を広げ、コミュニケーションを広げるやり方のヒントになればと思います。


行列の積

　さて、話題の軸に行列の積を選択したのは、行列を含む式が文章として表現しても、計算や変形を示し、説明するのが難しく、何より面倒くさいからです。

　行列の積をおなじみのスタイルで著してみましょう。
$${(n,m)}$$行列$${A=(a_{ij})}$$ と $${(m,l)}$$行列$${B=(b_{ij})}$$を,

$$
A =
\begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1m} \\
a_{21} & a_{22} & \cdots & a_{2m} \\
\cdots & \cdots & \cdots & \cdots \\
a_{n1} & a_{n2} & \cdots & a_{nm}
\end{bmatrix}, 
B =
\begin{bmatrix}
b_{11} & b_{12} & \cdots & b_{1l} \\
b_{21} & b_{22} & \cdots & b_{2l} \\
\cdots & \cdots & \cdots & \cdots \\
b_{m1} & b_{m2} & \cdots & b_{ml}
\end{bmatrix}
$$

と与えたとき、積$${C=AB=(c_{ij})}$$は

$$
c_{ij} = \sum_{k=1}^{m} a_{ik} b_{kj} 。
$$

より具体的に、

$$
C=
\begin{bmatrix}
a_{11} & \cdots & a_{1j} & \cdots & a_{1m} \\
\cdots & \cdots & \cdots  & \cdots & \cdots \\
a_{i1} & \cdots & a_{ij} & \cdots & a_{im}  \\
\cdots & \cdots & \cdots  & \cdots &  \cdots \\
a_{n1} & \cdots & a_{nj} & \cdots  & a_{nm} 
\end{bmatrix}
\begin{bmatrix}
b_{11} & \cdots & b_{1j} & \cdots & b_{1l} \\
\cdots & \cdots & \cdots & \cdots & \cdots \\
b_{i1} & \cdots & b_{ij} & \cdots & b_{il} \\
\cdots & \cdots & \cdots & \cdots & \cdots \\
b_{m1} & \cdots & b_{mij} & \cdots & b_{ml} 
\end{bmatrix}
=
\begin{bmatrix}
\sum_{k=1}^{m} a_{1k} b_{k1} & \cdots & \sum_{k=1}^{m} a_{1k} b_{kj} & \cdots & \sum_{k=1}^{m} a_{1k} b_{kl}  \\
\cdots & \cdots & \cdots & \cdots & \cdots \\
\sum_{k=1}^{m} a_{ik} b_{k1} & \cdots & \sum_{k=1}^{m} a_{ik} b_{kj} & \cdots & \sum_{k=1}^{m} a_{ik} b_{kl}  \\
\cdots & \cdots & \cdots & \cdots & \cdots \\
\sum_{k=1}^{m} a_{nk} b_{k1} & \cdots & \sum_{k=1}^{m} a_{nk} b_{kj} & \cdots & \sum_{k=1}^{m} a_{nk} b_{kl} 
\end{bmatrix}
$$

となります。

　これだけで50行ぐらい消費します。書いてる側にとってはコンテンツの全体像を見失う致命的な不便さです。(これはnote に限らず、数式を含むフォーマルな文体の記事に共通する問題に思えてなりません。)
　つまり、行列を話題にすることは、取りも直さず手書き計算を論じることになるだろう、という発想によるものです。
　以降は、本文に混ぜるTeX打ちの数式は最低限に留めます。

　行列の積の計算をちょっと見せておきましょう。字も計算もヘタと自任していますが、ここは数学でのインフォーマルな表現や議論を示す場としていますので、恥ずかしながらお見せしておきます。(本題とはほとんど関係がなく本当に恥ずかしいです)

行列の計算例(3次行列のLie括弧積の計算)

ちょっと詳しく見てみる

　行列の積をちょっと見直してみましょう。
　行列の積は、同じ個数の数２組$${(a_1,\cdots,a_n)}$$と$${(b_1,\cdots,b_n)}$$をそれぞれヨコ、タテに並べて掛け合わせる「計算単位」を組み合わせることでできあがっています。

行列の積を「計算単位」として見直す

https://x.com/tatatap2024/status/1869768444159435154

　本稿では、行列の積を「計算単位の組み合わせ」と見ていくことにより、思考の道具に使っていきます。順次取り上げていく「再構成」の話題に共通するのは行列計算を思考の道具として使う点です。
　行列の積を、要素を色分けするなどして表す工夫をしている文献は枚挙に暇がありませんが、ここでいう単位計算を組み合わせた記法は、[岡部・長谷川・村田]で積極的に取り入れられています。
　今回の記事を練るに当たり、同書を参考にさせてもらいました。
　なお、「計算単位」という言葉は私の思い付きで使っています。また、ここでの行列の積は、私がやっている「再構成」の動画で共通している見え方に過ぎず、特に新しい概念を取り入れて数学の手法や理論をつくり上げようというものではありませんのでご留意ください。

思い切って放り込んでみよう

　ここから計算を思考の道具として使い、線型代数の一般論の再構成をしていきます。
　まず、単位計算を表す式が線型結合(一次結合)であることに気付くと、行列の積が格段に使いやすくなります。

　一般に、行列の要素は体$${K}$$の元、加群をあつかう進んだ内容では環や$${K}$$代数$${R}$$と宣言しましたが、思い切ってベクトル空間の元を入れてしまいましょう。
　ただし、スカラーは左、右のどちらからからも同じく作用するものとしておきます。（なので係数が斜体や、非可換環上の加群は工夫が必要です）

線型結合、基底によるベクトルの表現

　ここでは表示の仕方にA案B案と２案ありますが、B案をとります。（理由は、後で出てくる双対性と、共変・反変と整合を図るため、あとは無理に監修に逆らう必要がないからです。）

　行列にベクトルを放り込む扱いは、私が学部生の頃から、誰に教わるわけでもなく何となくやってきたことです。しかし、線型代数の教科書に限って言えば、行列にベクトルを放り込んだり、ベクトルを並べてカッコで括ったりする扱いをしているものはほとんど見かけません。解説動画のいくつかで見かけるくらいですね。
　たぶん、教科書的には行列を「係数体$${K}$$上」と定義しているのでベクトルを入れることはありえないんでしょう。（こういった議論には関心がないので、このような記述に留めさせてください。）

線形代数の基本事項を再構成する

　ここからは、簡単な解説にとどめ「再構築」の作業をお見せしていきます。

基底の変換

　基底の変換です。基底の取り換え行列（変換行列）の正則性と、ベクトルの係数の反変性(contravariant)について述べています。

基底のとりかえ(変換)行列

線型写像

　線型写像の行列表示と、基底変換に対する挙動を整理しています。
　途中、計算上多用する線型写像と基底行列の交換が出てきます。

線型写像の行列表示

　ここで「教科書的な」公式が得られていないことに注意してください。
　うまくやれば教科書的な結果になりますが、線型写像を表す行列の要素は基底と結びつく係数で反変的な量なので、今の流れからいえばこちらが自然なような気がします。（ホントウかな…）

双対空間

　続いて双対空間です。双対基底の定義、基底変換による双対基底の挙動について整理しています。

双対空間と双対基底

　ここで、少し回りくどい言い回しですが、「双対基底の関係」と「双対空間の基底の取り換え行列」は違うものとして区別しています。

双対写像

　双対写像について整理しています。
　「行列の積」としては基底変換との関係とほぼ同じなのですが、多様体の余接空間の話題につながるので敢えて作りました。

双対写像

　線型代数の基本事項の再構成をお見せするのはこの辺にしておきます。
　実は計量空間の議論も入れ込むつもりだったので、双対基底の扱いを慎重にしており、ちょっと回りくどい言い回し、慣れない書き方をしているかと思います。
　予定していた計量空間は、noteにしてはボリュームが多く見えてきた（のと、継続的なコンテンツ配信に向けて余力を残したい）ので今回は見送ります。今後の展開にご期待ください。

　ここからは線形代数を離れ、扱った行列の計算が局面として現れる話題を紹介していくことにします。
　本来なら、読み手（受け手）を想定した解説動画や論説のように、丁寧に説明したいところなのですが、手作業を眺めていただくことが主旨なので、
準備はそこそこにしています。
　一つ一つの動画は高々15秒です、まだご存じない方や興味のない方も、「ああ、こうやって進むのかぁ～」なんて風に見ていただけると、ウマい／ヘタ、ごまかしてるとか間違えてたみたいなところを埋めていく風景を楽しんでいただければと思います。

接ベクトルと余接ベクトル

可微分関数と接空間

　接ベクトルの基底表現を整理しています。接ベクトルの定義を少々ぼやかし、座標関数により接空間の基底を構成できるという事実を用いています。
　ちなみに私は多様体の局所座標の図が好きなので、コピペなど使わずなんども描いています。

滑らかな関数と接空間

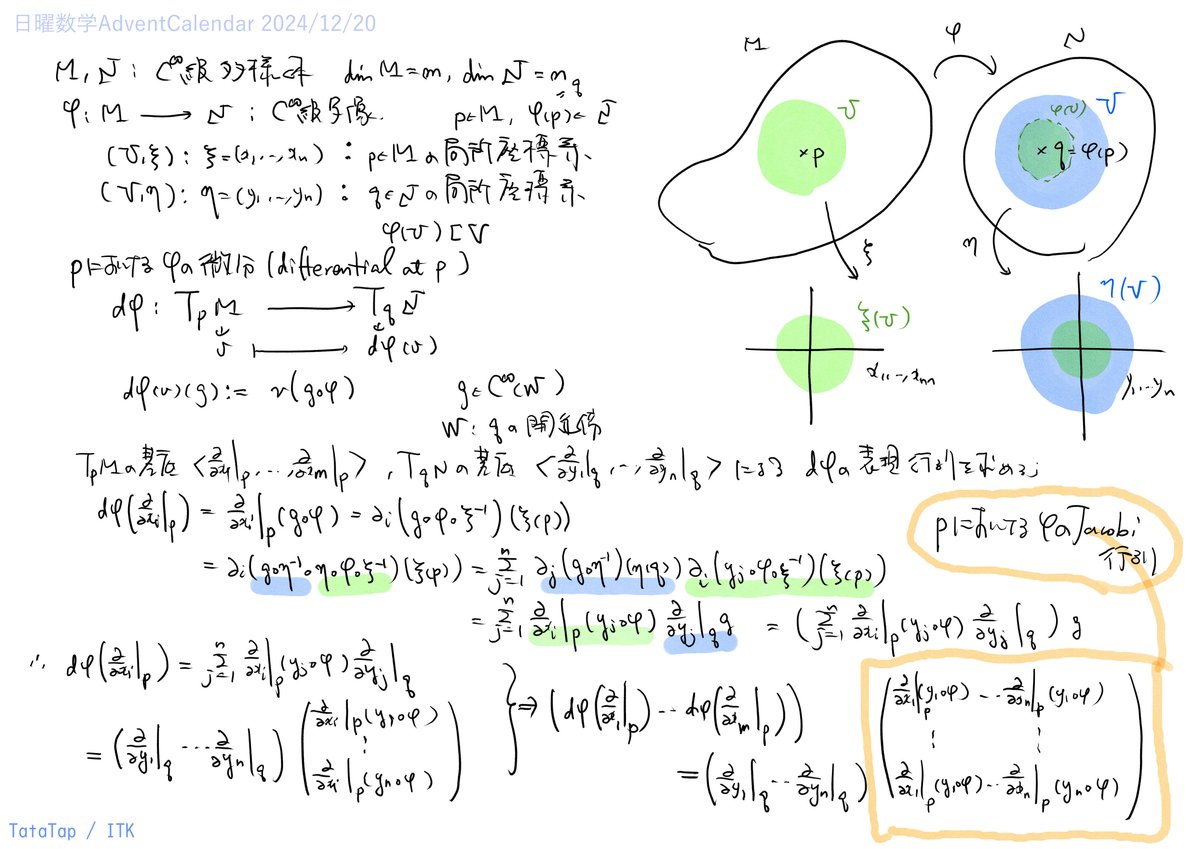
写像の微分

　接空間の線型写像を与える可微分写像の微分について整理しています。

滑らかな写像の微分

 ここで注意していただきたいのは、座標変換の規則で現れる行列は、決して行列の計算規則から生まれたものではないという点です。
　$${\mathbb{R}^{n}}$$上の$${C^{\infty}}$$関数に関する連鎖律により、異なる座標の接ベクトルという”微分作用素”を一次結合で表すことができるという事実が導かれ、行列の規則と適合しているのです。
　行列の規則と適合しているかどうかのチェックは、別の理論（ここでは微分積分・解析）を使ってやるということですね。当たり前に計算してしまっているので見落とされがちですが、この点を誤ってはいけません。

余接空間

　接空間の双対空間である余接空間と、可微分写像の微分の双対写像について整理しています。

余接空間

　どうでしょうか。
　単位計算で線型結合を表す、という操作ばかりでちょっと飽きてきたかもしれません。（私はちょっと飽きています。）
　しかしながら、どの分野も、新しい概念が次々と投入されるようなことはなく、似たような計算を何度も繰り返し、少しづつ理論が進んで行くものですので、こうしてしつこくやった方がいい気もします。（やった方がいいです。）
　ここで触れた内容は、[松本]や[松島]でおなじみのものです。どちらも必要なことは本題を外れてでも親切に記述していると思うのですが、結局うまくいくような書き方しかしておらず、失敗を繰り返した上で自分なりの展開を会得するには向かないかもしれません。
　個人的には、もっと泥臭く、遠回りした方が視点が広がって楽しくなると思っています。線型代数の範囲であれば[杉浦・横沼]、運動など物理的イメージを含めた展開では[田代]などが参考になります。
　[田代]を引き合いにしたので補足しますと、計量空間をあつかいたかったのはこのような話題を続け、最終的にはLaplacianの計算まで続けるつもりだったのです。
　ただ、このまま続けるとここまでの3倍くらいのボリュームと手間を要するとわかったので、別の機会に、もう少しちゃんと工夫した解説記事を計画することにします。

加法圏とアーベル圏

　さて、もともと幾何と代数の話題でやると宣言していましたので、代数の話題に移り圏における射の行列記法を紹介程度にやってみましょう。
　圏は抽象的で、細かい定義が多いので、人に見せる記述には神経を遣います。しかし、はじめに宣言したとおり、今回の記事は「思考の見せ方」が主題になります。細かい定義などは飛ばしていきますので、様子を見てもらえればと思います。

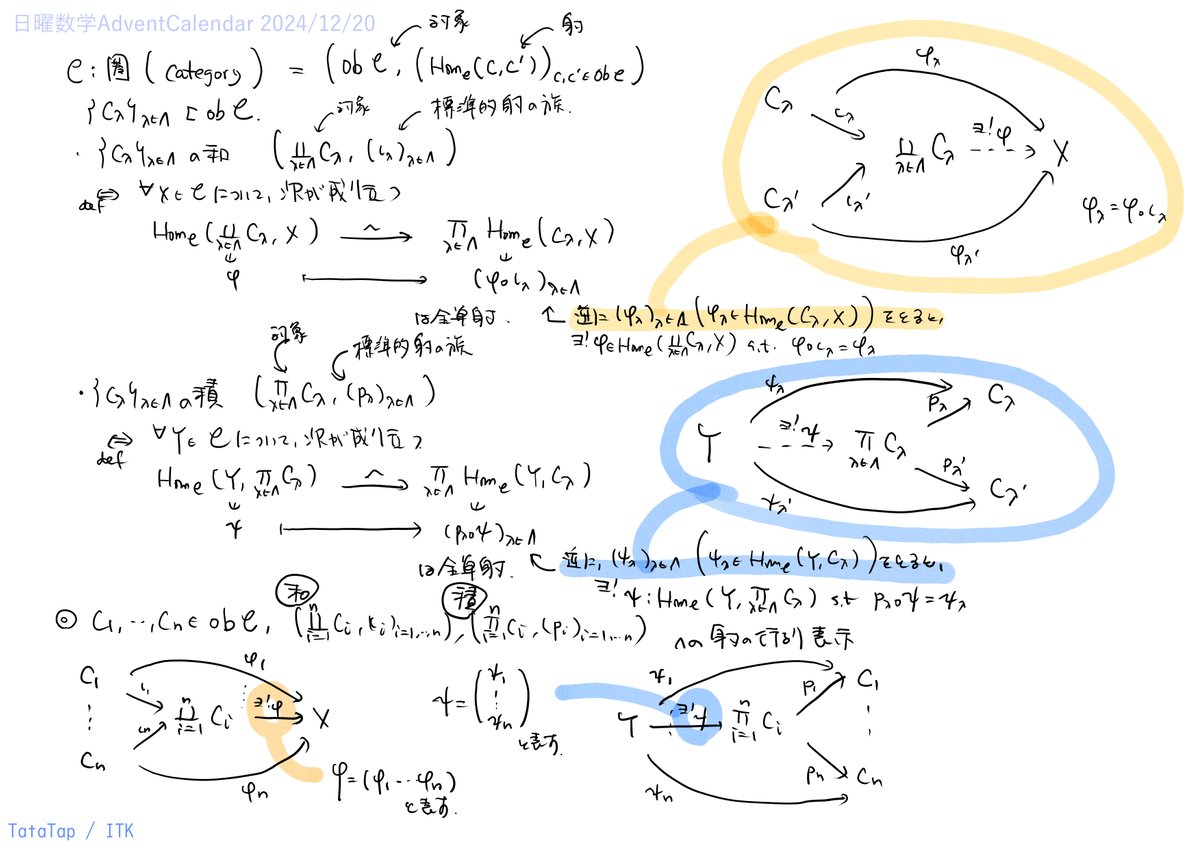
対象の和と積

　圏は、対象(object)と対象を結ぶ射(morphism)の集まりからなります。対象と射をあつかうので、集合の元のような扱いはありません。
　それでも、対象を直和のように組み合わせる和と、直積のように組み合わせる積を定義することができます。「条件を満たすものをそう呼ぶだけで、あるかどうかは問わない」という姿勢が強くあらわれるのが、圏を使った議論の特徴のひとつかもしれません。

対象の和と積

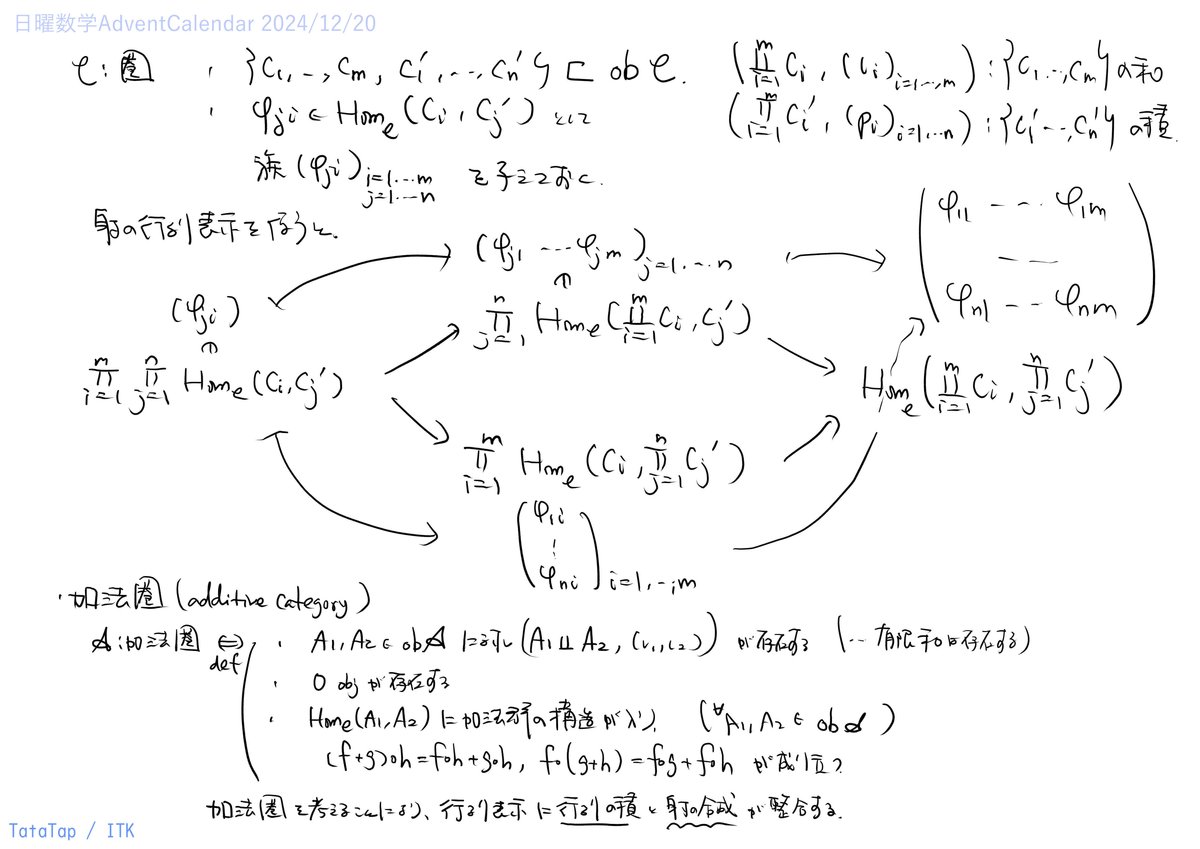
射の行列表示

　対象の和や積を議論するときの行列表示について整理しています。

対象の和・積における射の行列表示

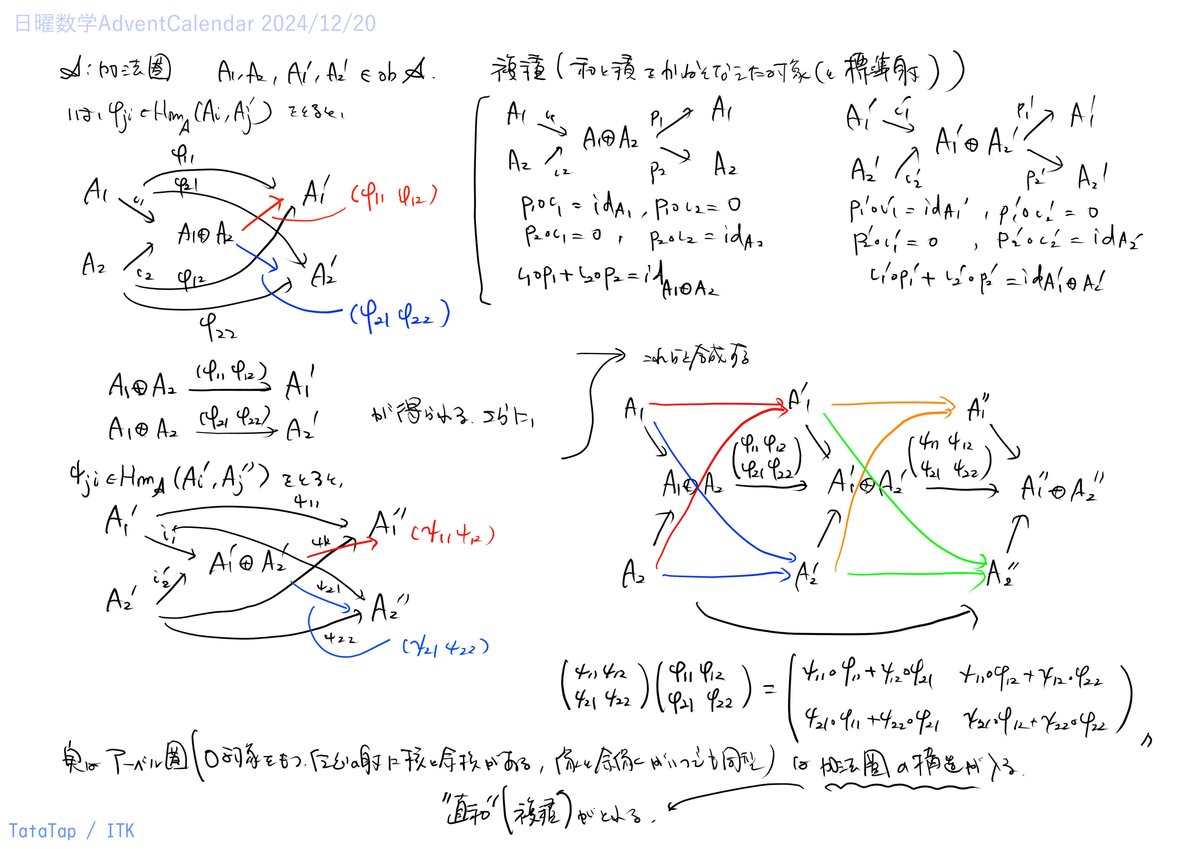
加法圈（とアーベル圈）

　加法圏における複積について整理しています。
　複積を通すことで、行列と行列の積がより抽象的な場でも使える道具であることがわかります。

加法圏、複積と射の行列表示

　最後に、行列の積がもうハッキリと現れるところを整理します。
　とはいえ、最後になってしまいましたので、本当の「再構成作業」という形で明示します。実はここまでお示ししたものは、文献の参照はほとんどしなかったものの、間違いや手戻り、レイアウトが悪いなどの理由で書き直しています。これだけは、ぶっつけ本番でやり直しなしです。
　最後は、特に見せるために取り繕わず、目標となる事実に向かった再構成をしてみた結果と過程をお見せしておきたいと思います。

とにかく再構成してみた

　以上の話は、[河田]、[志甫]に詳しいです。
　直和と直積、それらの普遍性などは、学部学生の頃から何とも腑に落ちず何年もごまかしてきましたが、複積を知って納得できました。そんなわけでかなり好きな話題ですので、そのうち解説記事を作ろうかとおもいます。楽しみにしていてください。

むすび

　いかがでしたでしょうか。
　もともと、動画で計算を見せる、あるいは論理や図式の展開を明示するというアイディアは、論文調の書き物を補足するのに有用じゃないかと思い立ったものです。

　液タブを使っていろいろと試しているうちに「計算って人に見られながらじゃ落ち着かないけど、人がどうやってるかは見てみたいなぁ」とか「頭の中を覗いた気分になって楽しそうだな」なんて思うようになり、人のを見たいのなら、まず自分の手の内を晒そう、という感じで今回の投稿に至りました。
　単純なテーマを選んだのも、字やレイアウトを気にせず、きれいに丁寧に、という方針をとらなかったのも、脇の甘い創作物を公開すれば、肩肘張らずともいいもの作る人があらわれるんじゃないか、という勝手な期待によるものでもあります。

　自己紹介もなく、これまでの取組みをほとんど表に出さないまま、noteの記事を作り、公開してしまいました。私が何者かについては、今後このnoteの場でお伝えします。また、来年(2025年)は、本文中で約束した記事をより善いものにするため、勉強、研究、試行錯誤をして形にしていこうと思います。

　今後ともよろしくお願いいたします。

参考文献

  • [岡部・長谷川・村田] 岡部恒治, 長谷川愛美, 村田敏紀, 『連立方程式から学ぶ行列・行列式 意味と計算の完全理解』, 共立出版(2014)

  • [河田] 河田敬義, 『ホモロジー代数』, 岩波書店(1977)

  • [佐武] 佐武一郎, 『線型代数学』, 裳華房(1958 ※33版1975)

  • [齋藤] 齋藤正彦, 『線型代数入門』, 東京大学出版会(1966 ※38刷1994)

  • [志甫] 志甫淳, 『層とホモロジー代数』, 共立出版(2016)

  • [杉浦・横沼] 杉浦光夫・横沼健雄, 『ジョルダン標準形・テンソル代数』, 岩波書店(1990)

  • [田代] 田代嘉宏, 『テンソル解析』, 裳華房(1981)

  • [松島] 松島与三, 『多様体入門』, 裳華房(1965)

  • [松本] 松本幸夫, 『多様体の基礎』, 東京大学出版会(1988)

いいなと思ったら応援しよう！