
自然言語処理を分かりやすくほぐして解説してみた👩💻
NLPとは?
まず自然言語(NL,Natural Language)とは大まかに私たちが普段話す日本語や英語といったような「人間が話す言語」のこと。(自然に形成された言語)
自然言語処理(NLP,Natural Language Processing)とはこうした言語を処理し利用する研究内容。恐らく一番イメージしやすいのはChatGPTであろう。ChatGPTやSiriのように人間の言葉の意味を理解して、回答を返すタイプのAIは自然言語処理の最先端技術なのである。そして世界中の巨大テック企業が莫大な資金をかけて今集中しているのがまさにこの分野といっても過言でない。💸💸💸
NLPの学び方
しかし、技術の急激な成長といった背景もあり、日本の理系大学を含め日本語で詳しく自然言語処理について学ぶことが出来る教材、環境は現状かなり少ない。実際に私が通っている東京工業大学、情報理工学系でも自然言語処理に特化した学部授業はない。
日本語のテキストでも個人的には数式の羅列ばかりで理解するのにかなりの労力と根性が試されるように感じている。
一方で海外の大学では学部から多様な自然言語処理に関する授業が開講されており、その上授業資料を公開していることが多い。
英語が堪能で英語の教材で十分勉強出来るのであればこれを使うことが最も最先端で詳しく学習することが出来る。
しかし、そうでないならば英語の部分は筆者に任せて、このnote型教材を使うことで日本語で詳しく学ぶことが出来る🙌
本noteでは自然言語処理(NLP)について、よくある感覚的に自然言語処理を学ぶといったことをはるかに超えて、
「理系として仕事として使うことが出来るように根底まで理解する」
を目標に大学1年レベルの数学で理解出来るように補足を十分加え、話の体裁を日本人に分かりやすいように出来るだけ整えています。現状、日本語で書かれたNLPに関する教材はかなり少ないので是非有効に活用して、今熱いNLPエンジニアとしてのキャリアをスタートしてみてはいかがでしょうか。

NLPのタスクの具体例
NLPタスクの具体例は以下のようになる。下に行くほど難易度の高い分野になる。
誤字チェック
文字検索(サイト上で一致する文字を検索)
web検索(Google検索など)
機械翻訳
質疑応答(ChatGPTなど) 👈最先端!!
Chapter 1: Word Vectors
NLPタスクの最初の関門で最も重要な課題の1つは
「単語をどのように表現するか」
である。
NLPももちろん機械学習(つまりAI)なので、コンピュータを使った計算をして学習をする必要がある。その際に人間の言葉のままだと足し算引き算をすることが出来ないのである🙅♀️。
そこでそれぞれの単語をベクトルに変えることから考える。この単語をベクトルに変換したものをword vectorという。
最も簡単な方法はone-hot vectorという方法である。
chapter 1-1 : one-hot vector
全ての単語を互いに独立なベクトルで表現する方法である。
具体例としては以下のように、

ある要素だけが1で他の全てを0とするベクトルで表現する方法である。
しかし、この方法は欠点だらけであった。その理由として👇
❌表現出来る単語の数に限りがある
N次元のベクトルを用意した場合はN個の単語しか表現できない。英語を表現するのには1300万の次元必要と言われており、工夫すれば次元を減らせるかも
❌単語間の類似度等を表現できない
単語には意味の間に類似度がある。
例えば、catとdogの2単語は動物,名詞といった観点から見ると類似度が高い。一方でcatとfromでは類似度はほとんどない。one-hot vectorでは任意の2つのベクトルが直行しており、距離も1であるので類似度を表すことが出来ない。これでは単語の意味をベクトルとして正しく反映出来ているとは到底言えない。
chapter 1-2 :Word-Document Matrix✖️特異値分解(SVD)
以上の事から、それぞれの単語について意味や類似度などの特性に着目して最適なword vectorを作ろうというのが自然な流れになります。そこで登場するのがWord-Document Matrixと特異値分解(SVD,Singular Value Decomposition)の合わせ技です。ここからかなり複雑で面白くなってくるので噛み砕いて順番に考えていきましょう👉
大学1年レベルの数学で理解出来るように補足を十分加え、すべての説明は簡単な具体例をベースに説明しています。
それを実現するのに数ヶ月の努力と根性、莫大な睡眠時間の損失によりこの記事が完成しました。
是非あなたの素晴らしいやる気と共にNLPエンジニアの世界にお入りください👇👇
⚠️この記事はお試しで¥0にしています。いいねやサポートを頂ければ続編も執筆致します🙇♀️
まず、根底にある考え方として「繋がりの強い単語はその周辺に出てくるだろう」という仮定を置いています。
例えば、"bank"(銀行),"money"(お金),"stock"(株式),"economy"(経済)といった言葉は近くに現れることが多いが、"bank"(銀行),"banana"(バナナ),"doraemon"(ドラえもん)といったあまり関係のない単語は近くには現れにくいということです。
この「繋がりが強いと近くに現れる」という考え方を「直前後に現れる」と絞って考えるのが今から考えるWord-Document Matrixの典型例です。
どういうことかというと、"I"の直後には動詞である"like"や"play"などがくる可能性が高く、逆に"panda"や"banana"などの名詞は可能性的には低くなります。
この事から、"I"と"like"の間の繋がりは"I"と"panda"の間よりも強いと言えるでしょう。
ここで、"I"と"like"は全く異なる意味ではないかと思った方がいるかもしれません。確かに辞書に載っているような意味的には全く異なるのですが、単語の位置的に見ると強い繋がりを持っているのです🙆♀️
実際にWord-Document Matrixの作り方を見ていきましょう。
例えば以下のような3つの文章が与えられた場合、
I like tennis.
I play the piano.
I like NLP.
3つの文章全体で見て、
◎"I"の直前後に来ている単語は "like"が2回,"play"が1回
◎"like"の直前後に来ている単語は"I"が2回,"tennis"が1回,"NLP"が1回
といった情報を元に以下のような行列を作成します👇

これが、Word-Document Matrixになります。
⚠️今回は直前後の単語だけを数えたのでwindow size=1となります。window sizeとはその単語から見て何単語分までを数えたのかという数値です。
例えば、仮にその単語から見て2単語までの範囲で数えた場合はwindow size=2となります。window size=2の場合は"like"の周囲には"I"が2回,"tennis"が1回,"NLP"が1回に加えて"."が2回も含まれます。
このまま行に着目して"I"に対応するword vectorは[0,2,0,1,0,0,0,0]
"like"は、[2,0,1,0,0,0,1,0],tennisは[0,1,0,0,0,0,1,0]のように作成することも出来ます🙆♀️
ただ、実際のNLPでは単語の数は10の6乗で数億に登るため、あまりに次元が膨大になってしまいます。
そこで特異値分解という方法を使って次元を減らすことが必須になります。
全体の大枠の流れとしては、
文書を元にWord-Document Matrixを作成する (👈説明済み)
Word-Document Matrixを特異値分解して次元を減らす
特異値分解によって作成した行列からword vectorを得る
となります。
次章に行うのが特異値分解(SVD,Singular Value Decomposition)になります。
特異値分解???となった方大丈夫です😏基礎から解説いたします。
⚠️もし特異値行列についてよく知っている方は飛ばしてください。機械学習で重要な考え方なので一読することを強くお勧めします🙇♀️
chapter 1-3: 特異値分解(SVD)とは🧐
特異値分解は機械学習でよく使われる行列の計算方法の1つで、定義は
であり、任意の行列はU,Σ,Vの行列の積に分解出来るというものになります。
とはいっても文字だけでは全く理解できないので図を使いながら順番に追っていきましょう👇
$${A=UΣV^T}$$
A: 任意の行列(m×n)
U:直行行列(m×m)
Σ:対角成分が非負で降順であり非対角成分が0である行列(m×n)
V:直行行列(n×n)
具体例としては以下の様になります。
$$
\begin{pmatrix}
3 & 2 & 2\\
2 & 3 & -2
\end{pmatrix}
=
\begin{pmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}}
\end{pmatrix}
\begin{pmatrix}
5 & 0 & 0\\
0& 3 & 0
\end{pmatrix}
\begin{pmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \\
\frac{1}{\sqrt{18}} & -\frac{1}{\sqrt{18}}& \frac{4}{\sqrt{18}}\\
\frac{2}{3} & -\frac{2}{3} & -\frac{1}{3}
\end{pmatrix}
$$
$$
\begin{pmatrix}
0 & 1 & 0 & 0\\
0 & 0 & 2 & 0\\
0 & 0 & 0 & 3\\
0 & 0 & 0 & 0\\
\end{pmatrix}
=
\begin{pmatrix}
0 & 0 & 1 & 0\\
0 & 1 & 0 & 0\\
1 & 0 & 0 & 0\\
0 & 0 & 0 & 1\\
\end{pmatrix}
\begin{pmatrix}
3 & 0 & 0 & 0\\
0 & 2 & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 0\\
\end{pmatrix}
\begin{pmatrix}
0 & 0 & 0 & 1\\
0 & 0 & 1 & 0\\
0 & 1 & 0 & 0\\
1 & 0 & 0 & 0\\
\end{pmatrix}
$$
では詳しくU,Σ,Vについての条件を見ていきましょう。
まず、U,Vについて
U,Vが直交行列となるわけですが、分かりやすく言えば、UはAの行空間を表したもの、VはAの列空間について着目したものです。なぜそうなるかについては後述のQiitaをご覧ください👀
そして、Σについて、
Σは以下のように大きい順に特異値を並べたものになります。

この𝜎𝑖は特異値と呼ばれAの階数(rank)に等しい数存在します。
これ以上の詳細はnoteでは数式が書けず説明が難しいのでQiitaに詳しく書きました。特異値分解は機械学習でかなり重要なのでぜひご覧ください。👇
特異値分解のWord-Document Matrixへの適用
そしていよいよ特異値分解をWord-Document Matrixにどのように適用するのかについて考えていきましょう。
そこでまず、特異値分解を意味的な観点から整理していきます!
まず、特異値分解とは、
$${A=UΣV^T}$$
A: 任意の行列(m×n)
U:直行行列(m×m)
Σ:対角成分が非負で降順であり非対角成分が0である行列(m×n)
V:直行行列(n×n)
ここで、Word-Document MatrixをAの行列として特異値分解を適用します。この際Word-Document Matrixは正方行列なので、A,U,Σ,V全て同じ形でn×nになります。
$${A=UΣV^T}$$
A: 任意の行列(n×n)
U:直行行列(n×n)
Σ:対角成分が非負で降順であり非対角成分が0である行列(n×n)
V:直行行列(n×n)
特異値分解を行列の形で書くと以下の様になります

そして、行列の計算を進めると、以下の様になり、σごとの和に置き換えられます。

更に計算を進めると、

以上の様になります。前章の特異値分解の中でσは添え字が小さいほど数が大きいという性質についても紹介しました。

そのため、以下の様に右に行くほどσが0に近くなり、左の項ほどσは大きくなります。

実際のNLPでは𝐴は数億の次数をもつので、以下の様に特異値分解の右側の方の項はほとんど意味を為さないことになります。そのため、右側を考えないという近似

をすることが出来ます。次数をkまで減らすことが出来ています。

以上までがQiitaの内容のハイライトになります。ここまでの範囲でわからない箇所があった場合は必ずQiitaを参照してください!
かなり根本まで解説しているので一文字一文字を飛ばし読みせず、実際に手でノートに書いてみながら追う事をお勧めします🖊️

最後にword-vectorを近似した後のUから作成すれば終了です👇
前章で説明した通りA=UΣVのUはAの行を、VはAの列を表したものになります。
今回の場合、A(Word-Document Matrix)は行も列も単語を表している👇のでU'でもV'でもどちらでも良いのですが、U'からword-vectorを作成します。

U'はAを特異値分解した後で先ほど説明した近似を行いkまで次元を少なくしたものです。U'は行空間を表すのでその行ベクトルがそれぞれの単語に対応することになります。
図で表すと以下のようにword vectorを作成出来ます👇

ここまでがWord-Document Matrixを使ったword vectorの作成方法になります。
再度全体像を見て確認してみましょう!
文書を元にWord-Document Matrixを作成する
Word-Document Matrixを特異値分解して次元を減らす
特異値分解によって作成した行列からword vectorを得る
Word-Document Matrixの欠点と改善策
これまで説明してきたWord-Document Matrixも以下のような欠点がある。
それは、
✔︎更新しにくい
新たな単語を追加すると次元が変わってしまう
✔︎行列にすると次元が大きくなる
Word-Document Matrixにした時点で行列なので普通のword vectorの2乗の大きさになる(≒10^6 × 10^6)ため、計算過程のサイズが大きい
✔︎単語の頻度が不均一
Iやlikeのように頻繁に出現する単語とNLPなどそこまで多くは出現しない単語の間で差が生じてしまう。
✔︎特異値分解の計算コストが大きい
特異値分解は行列計算のためO(n^2)と大きい計算量を必要とするので時間がかかる。
✔︎Word-Document Matrixの多くの要素が0
基本的には"learn"と"NLP"のような関係のある単語より"NLP"と"doraemon"といった無関係な組み合わせの方が多いので行列のほとんどの要素は0になり容量の無駄がある。
解決策としては、
◎距離によって重みづけをする
紹介したWord-Document Matrixは直前後しか考えなかったが、それ以外の単語も考慮し、単語との距離が近いほど影響が大きくなるように重み付けする。(直前後の方が重みが大きく、距離が遠いほど重みを小さくする)
◎意味が乏しい単語を考慮しない
"the"などのように"NLP"や"like"ほどの意味を持たない単語を考慮しないことでノイズを減らせる可能性がある
解決策はこれだけではなく、次章で説明するような反復的に学習する"Word2vec"という方法により多くの欠点は解消出来ます🙌
chapter 1-4: Word2vec
この方法はこれまでに挙げてきた方法とは全く異なります。平たく言うと、「word vectorを機械学習で学習する」といった方法になります。
そのための前提知識として、まずはある文章の自然さを確率で表現するという点について説明します。
文章の自然さを確率で表現する
具体例を見てから詳細を考えてみましょう👀
文章A:
I like this pen.
文章B
bank Doraemon is tree.
文章Aと文章Bを見比べると文章Bが不自然であることに気づくと思います。これを確率に置き換えると、文章Aが生成する確率に比べて文章Bが生成する確率は極めて小さいと言うことになります。
もう少し具体的に考えると、例えば文章Aについて以下の様にword vectorを定めます。👇
$$
w_I = "I"のword\ vector
$$
$$
w_{like} = "like"のword\ vector
$$
$$
w_{this} = "this"のword\ vector
$$
$$
w_{pen} = "pen"のword\ vector
$$
$$
w_{END} = "."のword\ vector
$$
ここで、文章Aが生成する確率は、
$$
P(W_1 = w_I,W_2=w_{like},W_3=w_{this},W_4=w_{pen},W_5=w_{END})
$$
となります。ここで$${W_i = w_x}$$は文章のi番目にxという単語が存在する事象です。
例えば、$${W_1=w_I}$$は文章の1番目の単語が"I"であるという事象になります。
文章Aが存在するという事象は、
1番目の単語が"I"である
かつ
2番目の単語が"like"である
かつ
3番目の単語が"this"である
かつ
4番目の単語が"pen"である
かつ
5番目の単語が"."である
に等しいので、文章Aが存在する事象は、
$$
P(W_1 = w_I,W_2=w_{like},W_3=w_{this},W_4=w_{pen},W_5=w_{END})
$$
といった同時確率で表すことが出来ます。
同じように文章Bについても考えてみましょう。
文章B
bank doraemon is tree.
単語ベクトルを追加で以下の様に定義します。
$$
w_{bank} = "bank"のword\ vector
$$
$$
w_{doraemon} = "doraemon"のword\ vector
$$
$$
w_{is} = "is"のword\ vector
$$
$$
w_{tree} = "tree"のword\ vector
$$
この時、文書B(bank doraemon is tree.)の生成する確率は
$$
P(W_1 = w_{bank},W_2=w_{doraemon},W_3=w_{is},W_4=w_{tree},W_5=w_{END})
$$
の様に表せます。
先ほど述べた、
文章Aと文章Bを見比べると文章Bが不自然であることに気づくと思います。これを確率に置き換えると、文章Aが生成する確率に比べて文章Bが生成する確率は極めて小さいと言うことになります。
とは、$${P(W_1 = w_I,W_2=w_{like},W_3=w_{this},W_4=w_{pen},W_5=w_{END}) }$$は大きく、$${P(W_1 = w_{bank},W_2=w_{doraemon},W_3=w_{is},W_4=w_{tree},W_5=w_{END}) }$$を小さくなります。
ここまでで文章を確率で表現するということを理解出来たでしょうか🧐
Word2vecはこの文書の自然さを確率で表した後、正解データと照らし合わせることでword vectorを学習するという方式になります。
先の例を使って説明してみましょう👇
文章Aの生成確率
$${P(W_1 = w_I,W_2=w_{like},W_3=w_{this},W_4=w_{pen},W_5=w_{END}) = 0.2}$$
であるとします。しかし、実際は文章A(I like this pen.)はかなり自然な文章であり、十分生成する可能性が高いので生成確率は1に近いはずです。
そのため、それぞれのword vector $${w_I,w_{like},w_{this},w_{pen},w_{END}}$$を$${P(W_1 = w_I,W_2=w_{like},W_3=w_{this},W_4=w_{pen},W_5=w_{END})}$$が大きくなるように変化させます。
逆に、文章Bの生成確率が、
$${P(W_1 = w_{bank},W_2=w_{doraemon},W_3=w_{is},W_4=w_{tree},W_5=w_{END}) =0.9}$$
であったとします。実際は文章B(bank doraemon is tree.)は不自然であるので生成確率は低いはずです。そのため、これらの値が低くなるようにword vector($${w_{bank},w_{doraemon},w_{is},w_{tree},w_{END}}$$)を変化させます。
このように正解データと照らし合わせながら繰り返しword vectorの値を変えることでword vectorの精度を高めるという方式がWord2vecになります。
Word2vecについてまとめると、
それぞれの単語に対するword vectorを適当な値で初期化する
ある文書に関して生成確率を求める。
文書の生成確率の正解データ(自然なほど1に近い)と照らし合わせて正解データの方向にword vectorを変化させる
2,3を何回も繰り返す
word vectorが完成する
という方式です。この方式は単語をベクトルに変える方法としてNLPでよく使われる手法なのでWord2vec 👉 "word to vec" 👉 "word to vector"(単語をベクトルへ)という名前の由来になっています。
ここで先の、
Word2vecについてまとめると、
1.それぞれの単語に対するword vectorを適当な値で初期化する
2.ある文書に関して生成確率を求める。
3.文書の生成確率の正解データ(自然なほど1に近い)と照らし合わせて正解データの方向にword vectorを変化させる
4.2,3を何回も繰り返す
5.word vectorが完成する
について2,3の部分について詳しくみていきましょう。
まず2の「ある文書に関して生成確率を求める。」について、生成確率の具体的な計算方法に関するアルゴリズムは主要なもので以下の2つがあります。👇
CBOW(continuous bag-of-words)
Skip-gram
また、3の「文書の生成確率の正解データ(自然なほど1に近い)と照らし合わせて正解データの方向にword vectorを変化させる」について、この過程を機械学習で「トレーニング」と言います。このトレーニングを効率化する方法が2つあり、
negative sampling
hierarchical softmax
になります。それぞれ具体的に見ていきましょう!!
Word2vecのアルゴリズム1 (CBOW)
CBOW(Continuous Bag of Words)は周囲の単語から中心の単語を推測するという方法になります。まずは具体例を見てみましょう👀
例えば、先ほど扱った文章Aについて
文章A
I like this pen.
例えば、中心の単語として"this"を予想したいとします。CBOWでは、
"I" "like" "pen" "."
↓
"this"
"this"の周囲の単語("I" "like" "pen" ".")から"this"を導くという方法になります。(window size=2)
(window sizeとは?となった方は「Word-Document Matrix✖️特異値分解(SVD)」を見てください。)
では詳しく数学的に見ていきましょう。
ここでCBOWではじめに混乱しやすい点を扱っておきます。それは、
CBOWではword vectorを直接予想するのではなくone-hot vectorを意味のあるword vectorに変換する行列を学習するという事です。
整理すると、
❌意味のあるword vectorが出力として得られる
⭕️one-hot vector を 意味のあるword vectorに変換する行列を学習する
になります。
具体的に考えてみましょう。
まず、以下の様にone-hot vectorを|V|×1で定義すると、
(|V|は後述の行列の大きさ)
$${x_I =\begin{pmatrix}1\\0\\0\\0\\0\\0\\ \vdots \\0\end{pmatrix},x_{like} = \begin{pmatrix}0\\1\\0\\0\\0\\0\\ \vdots \\0\end{pmatrix},x_{this} = \begin{pmatrix}0\\0\\1\\0\\0\\0\\ \vdots \\0\end{pmatrix},x_{pen} = \begin{pmatrix}0\\0\\0\\1\\0\\0\\ \vdots \\0\end{pmatrix},x_{END} = \begin{pmatrix}0\\0\\0\\0\\1\\0\\ \vdots \\0\end{pmatrix}}$$
そして、入力のone-hot vectorを意味のあるword vectorに変換する行列をVとし、その大きさをn×|V|とします。先ほど述べたように、
"this"の周囲の単語("I" "like" "pen" ".")から"this"を導くという方法になります。
より、入力は$${x_I,x_{like},x_{pen},x_{END}}$$になります。それぞれの意味のあるword vectorは以下の様になります。
$$
w_I = Vx_I,w_{like} = Vx_{like},w_{pen} = Vx_{pen},w_{END} = Vx_{END}
$$
ここでVはn×|V|,xは|V|×1なので、wはn×1のベクトルになります。
このVが学習するパラメータの1つになります。大事なことなのでもう一度説明すると、CBOWでは「one-hot vectorから意味を持つword vectorを生成するための行列」を学習するのであって、「word vector1つ1つを学習するわけではない」ということになります。
次にこれらの周囲の単語から"this"を予想します。予想の方法は単純で、周囲の単語の平均をとります。"this"の意味のあるword vector $${w_{this}}$$の予想値を$${\hat{w_{this}}}$$として、
$$
\hat{w_{this}} = \frac{w_I + w_{like}+w_{pen}+w_{END}}{4}
$$
となります。そしてこの「thisの意味のあるword vectorの予想値」($$\hat{w_{this}}$$)を 「thisのone-hot vectorの予測値」($${\hat{x_{this}}}$$)へと変換する行列をUとします。
その大きさは|V|×nです。
つまり、
$$
\hat{x_{this}} = softmax(U\hat{w_{this}})
$$
ここで使った$${softmax}$$関数はベクトルの値を0から1の間の値に変換する関数です。もし$${softmax}$$関数について分からない方は次の章に説明があるので先に読んでからここに戻ってきてください🙇♀️
softmaxを使う意味はone-hot vectorが0か1の値を持つためです。
正解データは先ほど定義した"this"のone-hot vector、
$$
x_{this} = \begin{pmatrix}0\\0\\1\\0\\0\\0\\ \vdots \\0\end{pmatrix}
$$
を用いるのでsoftmaxを使うことによって予測値$${\hat{x_{this}}}$$を0から1の間に限定し、正解データとの比較をしやすくしているのです。
ここまでで出力$${\hat{x_{this}}}$$が得られました。
後は学習になります。学習の過程では先ほど説明したVに加えてUも学習します。
Uの働きは、「意味を持つword vectorからone-hot vectorを生成するための行列」のイメージです。実際にはone-hot vectorを生成するためには最終的にsoftmax関数を挟むことに注意してください、
ここまでの流れをまとめると、
文書全ての単語についてone-hot vectorを定義する
予測したい単語の周囲の単語のone-hot vector($${x}$$)を"意味のあるword vector($${w}$$)"にVで変換する($${w=Vx}$$)
2で求めたwの平均を予測値とする($${\hat{w}}$$)
3で求めた予測値をone-hot vectorの予測値($${\hat{x}}$$)にUで変換する($${\hat{x}=softmax(U\hat{w})}$$)

学習のプロセスは損失関数を求めることから始まります。
損失関数とは一般的には「値が大きいほど予想と正解データの誤差が大きくなる」関数です。
CBOWでは以下のクロスエントロピー関数というものを使います。
$$
H(\hat{y},y) = -\sum_{k=1} ^n y_k log(\hat{y_k})
$$
但し、$${y}$$は正解データ(今回の例だと$${x_{this}}$$),$${\hat{y}}$$は予測値(今回の例だと$${\hat{x_{this}}}$$)になります。
クロスエントロピー関数は今回のようにone-hot vector間の予測値と正解データの誤差に関する学習でよく使われます。
クロスエントロピーについても補足としてこの章の後に載せているので、聞き馴染みのない方は一度そちらを一読してからここに戻ってくることをお勧めします🙇♀️
今回の場合に合わせると以下の式を最小にする問題に帰着します👇
$$
H(\hat{x_{this}},x_{this}) = -\sum_{k=1} ^{|V|} {x_{this}}_k log(\hat{{x_{this}}_k})
$$
後は損失関数を最小にする方向にVとUを更新すれば終わりです🙌
「損失関数を最小にする方向」は損失関数の勾配の逆方向です。
$$
V_{new} \leftarrow V_{old} - \alpha \frac{\partial H}{\partial V} \\
U_{new} \leftarrow U_{old} - \alpha \frac{\partial H}{\partial U}
$$
但し($${\alpha > 0}$$)
これを機械学習において勾配降下法(Stochastic gradient descent,SGD)といいます。
以下勾配降下法(Stochastic gradient descent,SGD)についての補足です。すでに知っている方は飛ばしてください🙇♀️

勾配方向とは現在地の接線方向です。その逆方向が極小値の方向になるので最小値問題では頻出で定番の方法になります。

そのため、上の図の例で現在地よりも極小値側にxを移動させたかったら以下の更新式を使います。
$$
x_{new} \leftarrow x_{old} - \alpha \frac{\partial f}{\partial x} \\
$$
ここで$${\alpha}$$は正の定数でどれほど移動するかということになります。
$${\alpha}$$が大きすぎると以下のように移動し過ぎてしまいます。

逆に小さすぎると極小値に到達するのに時間がかかり過ぎてしまうので適切な値を選択するのが大切です。
先ほどの議論で、「損失関数を最小にする方向」は損失関数の勾配の逆方向として以下の式を紹介しました。
$$
V_{new} \leftarrow V_{old} - \alpha \frac{\partial H}{\partial V} \\
U_{new} \leftarrow U_{old} - \alpha \frac{\partial H}{\partial U}
$$
では実際にクロスエントロピー$${H}$$の勾配を計算してみましょう。
$$
H(\hat{y},y) = -\sum_{k=1} ^n y_k log(\hat{y_k})
$$
ですが、簡単のため、one-hot vectorにおいて$${y_k = 1}$$となる$${k}$$を$${c}$$と置くと、他は0になるので
$$
H(\hat{y},y) = - log(\hat{y_c})
$$
ここで、$${\hat{y_c}}$$は以下のように求められました。
(補足1)softmax関数とは🧐
(以下$${softmax}$$関数の説明です。既に知っている方は飛ばしてください)
ここで使った$${softmax}$$関数はベクトルの値を0から1の間の値に変換する関数です。具体的には、xをn×1の以下のようなベクトルとすると、
$$
x =
\begin{pmatrix}
x_1\\ x_2\\ x_3\\ \vdots\\ x_n
\end{pmatrix}
$$
$${softmax(x)}$$は以下の様に定義されます。
$$
softmax(x_i) = \frac{e^{x_i}}{\sum_{k=1}^{n}e^{x_k}}
$$
つまり、ベクトルxに$${softmax}$$関数を作用させると以下の様になります。
$$
softmax(x) =
\frac{1}{\sum_{k=1}^{n}e^{x_k}}
\begin{pmatrix}
e^{x_1}\\
e^{x_2}\\
\vdots \\
e^{x_n}
\end{pmatrix}
$$
まとめると、以下のステップで求まります。
step1:各要素を指数関数にする
$$
\begin{pmatrix}
x_1\\ x_2\\ x_3\\ \vdots\\ x_n
\end{pmatrix}
\overset{\text{指数を取る}}{\rightarrow}
\begin{pmatrix}
e^{x_1}\\ e^{x_2}\\ e^{x_3}\\ \vdots\\ e^{x_n}
\end{pmatrix}
$$
step2:各要素の合計を求める。
$$
A = \sum_{k=1}^{n}e^{x_k} = e^{x_1} + e^{x_2} + \cdots + e^{x_n}
$$
step3:step1をstep2で割る
$$
softmax(x) = \frac{1}{A}
\begin{pmatrix}
e^{x_1}\\
e^{x_2}\\
\vdots \\
e^{x_n}
\end{pmatrix}
$$
$${e^{x_1},e^{x_2},\cdots, e^{x_n}}$$はそれぞれ正なので、それぞれの値はその合計$${A = \sum_{k=1}^{n}e^{x_k}}$$よりも小さくなります。
$$
0< e^{x_i} < A \ \ (i = 1,2,…,n)
$$
そのため、$${softmax(x)}$$の各要素は0~1の間になります。
$$
0< \frac{e^{x_i} }{A} < 1 \ \ (i = 1,2,…,n)
$$
以上のようにsoftmax関数を使うとベクトルの各要素を大小関係を変えずに0から1の値に変換することができます。
また、softmax関数は最後に各要素をすべての要素の合計$${A = \sum_{k=1}^{n}e^{x_k}}$$で割っているので、softmax関数適用後の全要素の総和は1になります。
$$
z=softmax(x)とし、
z=
\begin{pmatrix}
z_1\\
z_2\\
\vdots \\
z_n
\end{pmatrix}とすると、\\
\sum_{k=1}^nz_k = \sum_{k=1}^n\frac{1}{A} e^{x_k} = \frac{1}{A} \sum_{k=1}^ne^{x_k} = \frac{1}{A}A=1
$$
(補足2)クロスエントロピーとは🧐
クロスエントロピーとは何かということも含め具体例から考えてみましょう💪
まず、one-hot vector間の学習について、例えば、予測値を$${\hat{y}}$$,正解データを$${y}$$とします。
予測値が以下の様になったとき、
$$
\hat{y} =
\begin{pmatrix}
0.12\\0.01\\0.1\\0.48\\0.24\\ \vdots
\end{pmatrix}
$$
このとき、4番目の要素の0.48が最も大きい値になるので、one-hot vectorとしては、
$${\begin{pmatrix}0\\0\\0\\1\\0\end{pmatrix}}$$である可能性が高くなります。この「最も大きい値を持つ要素だけ1に、残りを0にする」というのが実際にクロスエントロピーを使った学習の際に使うone-hot vectorの考え方になります。
$$
\hat{y} =
\begin{pmatrix}
0.12\\0.01\\0.1\\0.48\\0.24\\ \vdots
\end{pmatrix}
→
\begin{pmatrix}0\\0\\0\\1\\0\\ \vdots \end{pmatrix}
$$
別の言い方をしてみましょう。正解データが以下の様であったとき、
$$
\hat{y} =
\begin{pmatrix}
0\\0\\0\\1\\0
\end{pmatrix}
$$
予測データ($${\hat{y}}$$)で着目するのは4番目の要素だけで良いのです。$${\hat{y}}$$の4番目の要素が大きければ大きいほど正解データと同じように分類される可能性が高くなるためです。
つまり、「2番目以外の要素の大小には着目せず、2番目のみ大きくすることを考える」という戦法をとっていることになります。
これを数式にして考えてみましょう。
まず、予測データ($${\hat{y}}$$)と正解データ($${y}$$)の要素を以下の様に定義します。
$$
\hat{y} =
\begin{pmatrix}
\hat{y_1}\\
\hat{y_2}\\
\hat{y_3}\\
\vdots \\
\hat{y_n}
\end{pmatrix}
\
y =
\begin{pmatrix}
y_1\\
y_2\\
y_3\\
\vdots \\
y_n
\end{pmatrix}
$$
先ほど述べたようにone-hot vectorの学習では予測値の内、「正解データが1の要素」だけに着目します。
以下のよう立式すると、予測値の内、「正解データが1の要素」だけが得られます。
$$
\prod_{k=1}^{n} \hat{y_k}^{y_k}
$$
なぜなら、$${ \hat{y_k}^{y_k}}$$は以下のような性質を持つためです👇
$$
\hat{y_k}^{y_k} = \hat{y_k} (y_k = 1のとき ) \\
\hat{y_k}^{y_k} = 1 \ \ \ \ (y_k = 0のとき)
$$
そのため、$${ \hat{y_k}^{y_k}}$$をk=1,2,…,nで積をとれば、正解データが1の要素($${y_k=1}$$)だけの $${\hat{y_k}}$$が得られます。
そして先の例のように、この得られた正解データが1である予測値の要素が大きければ大きいほど予測の正確さが増すので、$${\prod_{k=1}^{n} \hat{y_k}^{y_k}}$$を最大にしようという問題に帰着します。
しかし、この積の形はこの後の勾配を求めるために微分する時に計算が複雑になってしまいます。(積の微分公式を思い出してください)
そのため、対数をとって
$$
log (\prod_{k=1}^{n} \ \hat{y_k}^{y_k}) = \sum_{k=1}^{n} \ log \ \hat{y_k}^{y_k} = \sum_{k=1}^{n} \ y_k\ log \ \hat{y_k}
$$
となるので、$${\prod_{k=1}^{n} \hat{y_k}^{y_k}}$$の最大化問題は$${\sum_{k=1}^{n} \ y_k\ log \ \hat{y_k}}$$の最大化問題となるのです。
学習で用いる損失関数とは予測値と正解データの誤差を表す関数なので、「大きければ大きいほど正確ではなくなる」関数です。
一方、今求めた、「$${\sum_{k=1}^{n} \ y_k\ log \ \hat{y_k}}$$の最大化問題」は「が大きければ大きいほど正確になる」という問題になるので損失関数として使う場合は、-1を掛けて増減を逆にした
$$
H(\hat{y},y)= -\sum_{k=1}^{n} \ y_k\ log \ \hat{y_k}
$$
を使います。これをクロスエントロピー(cross entropy,交差エントロピー)と言います。
または、$${\sum_{k=1}^{n} \ y_k\ log \ \hat{y_k}}$$をクロスエントロピーといい、$${-\sum_{k=1}^{n} \ y_k\ log \ \hat{y_k}}$$を負の対数尤度(Negative Log-Likelihood, NLL)ということもあります。
Word2vecのアルゴリズム2(Skip-gram)
Word2vecにはもう一つアルゴリズムがありこれはCBOWを全く逆にしたものになります。
CBOWでは以下のように周囲の単語から中心の単語を予測しました。
"I" "like" "pen" "."
↓
"this"

今回議論するのはこの逆で、中心の単語から周囲の単語を予測します。
"this"
↓
"I" "like" "pen" "."

以上の例のように、"this"という単語が与えれられた時、その周囲の"I" "like" "pen" "."を生成するというアルゴリズムをSkip-Gramといいます。
アルゴリズムの中身もCBOWを概ね逆にしたものになります。
つまり、以上の"I like this pen."の例で言うと、
まず、以下の様にone-hot vectorを|V|×1で定義します、
(|V|は後述の行列の大きさ)
$${x_I =\begin{pmatrix}1\\0\\0\\0\\0\\0\\ \vdots \\0\end{pmatrix},x_{like} = \begin{pmatrix}0\\1\\0\\0\\0\\0\\ \vdots \\0\end{pmatrix},x_{this} = \begin{pmatrix}0\\0\\1\\0\\0\\0\\ \vdots \\0\end{pmatrix},x_{pen} = \begin{pmatrix}0\\0\\0\\1\\0\\0\\ \vdots \\0\end{pmatrix},x_{END} = \begin{pmatrix}0\\0\\0\\0\\1\\0\\ \vdots \\0\end{pmatrix}}$$
次に中心の単語について意味のあるword vector(n×1)を行列V(n×|V|)から作成します。
$$
w_{this} = Vx_{this}
$$
この意味のあるword vector(n×1)からその周囲の単語のone-hot vectorの予測値をU(|V|×n)と$${softmax}$$関数を使って作成します。
$$
\hat{x} = softmax(Uw_{this})
$$
ここからが少しだけ変わってくるので注意してください👀
今、$${\hat{x}}$$は、U(|V|×n)と$${w_{this}}$$(n×1)の積により、|V|×1のベクトルになります。その要素が以下のようであったとします👇
$$
\hat{x} =
\begin{pmatrix}
0.14\\0.17\\ 0.01\\ 0.29 \\0.09\\ \vdots
\end{pmatrix}
$$
これが何を表しているかというとそれぞれの要素に対応するone-hot vecotrを持つ単語が周辺にある確率です。これまでの例では、
$${x_I =\begin{pmatrix}1\\0\\0\\0\\0\\0\\ \vdots \\0\end{pmatrix},x_{like} = \begin{pmatrix}0\\1\\0\\0\\0\\0\\ \vdots \\0\end{pmatrix},x_{this} = \begin{pmatrix}0\\0\\1\\0\\0\\0\\ \vdots \\0\end{pmatrix},x_{pen} = \begin{pmatrix}0\\0\\0\\1\\0\\0\\ \vdots \\0\end{pmatrix},x_{END} = \begin{pmatrix}0\\0\\0\\0\\1\\0\\ \vdots \\0\end{pmatrix}}$$
を考えていたので、出力の$${\hat{x}}$$は以下のように表すことが出来ます。
$$
\hat{x}=\begin{pmatrix}
0.14\\0.17\\ 0.01\\ 0.29 \\0.09\\ \vdots
\end{pmatrix}\\
=0.14\begin{pmatrix}1\\0\\0\\0\\0\\0\\ \vdots \\0\end{pmatrix}+0.17 \begin{pmatrix}0\\1\\0\\0\\0\\0\\ \vdots \\0\end{pmatrix}+0.01 \begin{pmatrix}0\\0\\1\\0\\0\\0\\ \vdots \\0\end{pmatrix}+0.29 \begin{pmatrix}0\\0\\0\\1\\0\\0\\ \vdots \\0\end{pmatrix}+0.09 \begin{pmatrix}0\\0\\0\\0\\1\\0\\ \vdots \\0\end{pmatrix}+\cdots\\
=0.14x_I +0.17x_{like}+0.01x_{this}+0.29x_{pen}+0.09x_{END}+\cdots
$$
このようにしてみると"this"という単語の周りに
"I"の影響度が0.14,
"like"の影響度が0.17,
"this"の影響度が0.01
$${\vdots}$$
といったように見ることが出来ます。
softmax関数の性質から係数をすべて足すと1になるので、この「影響度」というのは確率に置き換えることが出来て、
このようにしてみると"this"という単語の周りに
"I"が存在する確率が0.14,
"like"が存在する確率は0.17,
"this"が存在する確率は0.01
$${\vdots}$$
といったように見ることが出来ます。
この確率というのは、前提として「中心の単語として"this"が与えられたとき」というのがあるので条件付き確率になります。上の文章を少し訂正すると以下のようになります。
$$
中心の単語として"this"が与えられたとき、"I"が存在する確率が0.14,\\
中心の単語として"this"が与えられたとき、"like"が存在する確率は0.17,\\
中心の単語として"this"が与えられたとき、"this"が存在する確率は0.01\\
\vdots
$$
これを式で書くと以下のようになります。
$$
P(w_I | w_{this}) = 0.14 \\
P(w_{like} | w_{this}) = 0.17 \\
P(w_{this} | w_{this}) = 0.14 \\
\ \ \ \ \ \ \ \ \ \vdots
$$
つまり、$${\hat{x}}$$の各要素は中心の単語として"this"が与えられたときを条件とする条件付きの存在確率を示しているのです。
Skip-gramによる出力($${\hat{x}}$$)の要素を以下のように定義すると、
$$
\hat{x} =
\begin{pmatrix}
\hat{x_1} \\
\hat{x_2} \\
\vdots \\
\hat{x_{|V|}} \\
\end{pmatrix}
$$
以下のように表せます。
$$
P(w_I | w_{this}) = \hat{x_1} \\
P(w_{like} | w_{this}) = \hat{x_2} \\
P(w_{this} | w_{this}) = \hat{x_3} \\
\ \ \ \ \ \ \ \ \ \vdots
$$
正解データは、"this"の周りが"I" "like" "pen" "."というものだったので、上で定義したone-hot vectorから$${\hat{x}}$$の内,1番目("I"),2番目("like"),4番目("pen"),5番目(".")が大きくなるほど誤差が少ないことになります。

そのため、これらの積をとって、
$$
P(w_I | w_{this}) × P(w_{like} | w_{this}) ×P(w_{pen} | w_{this}) ×P(w_{EMD} | w_{this}) = \hat{x_1} × \hat{x_2} × \hat{x_4} × \hat{x_5} =0.14 × 0.17 × 0.29× 0.09
$$
が大きいほど予想が正確ということになります。
一般的な書き方に変えると以下のようになります。
$$
P(w_I | w_{this}) × P(w_{like} | w_{this}) ×P(w_{pen} | w_{this}) ×P(w_{EMD} | w_{this}) = \prod_{k=1,k\neq 3}^{5} \hat{x_k}
$$
さらに、正解データである"I","like","pen","."の添え字の集合をDとすると、$${D = \{ 1,2,4,5 \}}$$となり、以下のように表せます。
$$
\prod_{k=1,k\neq 3}^{5} \hat{x_k} = \prod_{k \in D} \hat{x_k}
$$
CBOWの際に説明したように、学習の時に積があると微分の計算が大変になるので対数をとって、
$$
log\prod_{k \in D} \hat{x_k}=\sum_{k \in D} log\hat{x_k}
$$
となり、これが大きいほど予測の精度が高くなります。
学習の際には損失関数として、「小さいほど精度が高くなる」ようにしたいので-1を掛けたものを損失関数(L)として利用します。
$$
L = -\sum_{k \in D}log \hat{x_k}
$$
後は勾配降下法により更新をすれば完了です。
$$
V_{new} \leftarrow V_{old} - \alpha \frac{\partial L}{\partial V} \\
U_{new} \leftarrow U_{old} - \alpha \frac{\partial L}{\partial U}
$$
Word2vecの効率化1(negative sampling)
Word2vecはone-hot vectorを使うのでone-hot vectorにまつわる問題点がそのまま残ります。それは、単語の数だけone-hot vectorの次元が大きくなるため実際に利用する際には|V|が莫大な大きさになってしまい、それに伴う計算量が膨大であることです。
そのため、UとVの更新を繰り返してしまうと莫大な時間が掛かってしまい実用性に欠くことになります🕰️
そこで、1回ごとの更新の計算量を少なくしようといった改善の1つとしてnegative sampling(ネガティブサンプリング)が良く用いられます。
代表的なのがSkip-gramに用いられたものでSkip-gram with Negative Sampling (SGNS)と呼ばれます。これについて具体例を見て解説していきます👇
まず、思い出して欲しいのがSkip-gramの損失関数において「注目するのは正解データで登場する単語のみでその他の大きさは気にしない」というスタンスでした。
これまでの例でいうと、Skip-gramでは
"this"
↓
"I" "like" "pen" "."
を学習するというものでした。Skip-gramによる出力($${\hat{x}}$$)の要素を以下のように定義すると、
$$
\hat{x} =
\begin{pmatrix}
\hat{x_1} \\
\hat{x_2} \\
\vdots \\
\hat{x_{|V|}} \\
\end{pmatrix}
$$
着目するのは"I","like","pen","."のone-hot vectorに対応する1,2,4,5番目($${\hat{x_1},\hat{x_2},\hat{x_4},\hat{x_5}}$$)のみでした。
(下図の右側赤く塗りつぶしてある丸)

これらの大きさが大きければ大きいほど良いという学習法でした。その他の値の大きさについて気にしなかった理由としてはsoftmax関数の性質にあります。softmax関数によって$${\hat{x}}$$の要素の和が1となっています。
$$
\sum_{k=1}^{|V|}\hat{x_k} = 1
$$
そのため、着目している$${\hat{x_1},\hat{x_2},\hat{x_4},\hat{x_5}}$$が大きければ大きいほど、それに対応してその他の値は小さくなることになります。
しかし、それと同時にsoftmax関数の計算のためにすべての要素の指数を計算する必要があり|V|に比例する計算量(O(|V|))が必要になります。
これを効率化するために$${softmax}$$の代わりに$${sigmoid}$$関数(シグモイド関数)というものを使います。
以下シグモイド関数の説明です。知っている方は飛ばしてください🙇♀️
シグモイド関数の定義は以下の通りです👇
$$
\sigma(x) = \frac{1}{1+e^{-x}}
$$
$${\sigma(x)}$$はシグモイド関数を表すためによく使われる記法で本noteでも以下使用します。
グラフは以下の通りで$${0<\sigma(x)<1}$$の値をとります。

単調増加関数のため大小関係を変えることなく、どんな値を入れても1を超えず、0を下回らないことから確率表現として重宝されます。
(シグモイド関数の補足終わり)
negative sampling(ネガティブサンプリング)では$${softmax}$$関数の代わりにシグモイド関数を各要素に対して使います。

しかし、すべての要素について適用するのではなく、"I","like","pen","."に対応する$${\hat{x_1},\hat{x_2},\hat{x_4},\hat{x_5}}$$と「その他」の単語からランダムに数個選んだ要素にのみ適用しこれらが計算に使われます。
ランダムな選び方についてはこの章の最後にまとめてあります。
そして、正解データに対応する$${\hat{x_1},\hat{x_2},\hat{x_4},\hat{x_5}}$$は大きくなるように、逆に、
「その他」からランダムに選んだ数個は小さくなるように
学習をすることで毎回の学習の更新における正確さは下がるが更新時の計算量が小さくなるという方法になります。
普通のSkip-gramとの違いを繰り返し伝えておくと、普通のSkip-gramではsoftmaxを使ったことで$${\hat{x_1},\hat{x_2},\hat{x_4},\hat{x_5}}$$は大きくなり、その他は合計として小さくなりました。
一方negative sampling(ネガティブサンプリング)では、シグモイド関数を使い、$${\hat{x_1},\hat{x_2},\hat{x_4},\hat{x_5}}$$を大きくするのですがこれだけではその他の値まで大きくなってしまう可能性があります。(softmaxのように全体の和が1にならず個々が独立しているため)
そこでその他の内から数個ランダムで取ってきてこれらが小さくなるように学習に組みこむのです。
実際に具体例を見てみましょう。
選び方は一度置いておいて、例えばnegative sampling(ネガティブサンプリング)として"money","clock"が選ばれたとします。そして、"money","clock"のone-hot vectorは以下のように定めます。
$${x_{money} =e_6,x_{clock} = e_7}$$
ここでnegative sampling(ネガティブサンプリング)によって選ばれた単語の添え字の集合を$${\bar{D}}$$とし、$${\bar{D}\in \{ 6,7 \} }$$となります。
⚠️ここで$${e_i}$$はi番目の要素が1のone-hot vectorとし、例えば、以下のようになります。👇
$${e_1 =\begin{pmatrix}1\\0\\0\\0\\0\\0\\ \vdots \\0\end{pmatrix},e_{2} = \begin{pmatrix}0\\1\\0\\0\\0\\0\\ \vdots \\0\end{pmatrix},e_{3} = \begin{pmatrix}0\\0\\1\\0\\0\\0\\ \vdots \\0\end{pmatrix},e_4 = \begin{pmatrix}0\\0\\0\\1\\0\\0\\ \vdots \\0\end{pmatrix},e_{5} = \begin{pmatrix}0\\0\\0\\0\\1\\0\\ \vdots \\0\end{pmatrix}}$$
先の例で"I","like","this","pen","."は以下のように表せます。
$${x_I = e_1,x_{like} = e_2,x_{this} = e_3,x_{pen} = e_4,x_{END} = e_5}$$
Skip-gramでは以下のような評価関数が元にありました。
$$
\prod_{k \in D} P(w_k | w_3) = \prod_{k \in D} \hat{x}_k
$$
ただし、$${D \in \{ 1,2,4,5 \}}$$です。
正解データにある単語("I","like","pen",".")に対応する$${\hat{x}}$$の要素が大きければ大きいほど良いというアルゴリズムでしたので、Skip-gram with Negative Sampling (SGNS)では、これに「その他が小さければ小さいほど良い」と言う考え方を加えます。今回は"その他"として"money","clock"の二単語が選ばれたので、これらが小さければ小さいほど良いと言うことはこれらの要素が「0に近ければ近いほど良い」ということになるので、
$$
(1-\hat{x_6})(1-\hat{x_7})
$$
が大きければ大きいほど良いことと等価になります。
($${\hat{x_6}}$$が0に近ければ近いほど$${1-\hat{x_6}}$$は1に近くなるためです。)
ここで、「その他」の中から無作為に選んだ単語たちの添字の集合を$${\bar{D}}$$とすると、今回は"money"と"clock"が選べれ、それぞれの添字は6,7なので、$${\bar{D} = \{6,7\}}$$になります。これを使って、
$$
(1-\hat{x_6})(1-\hat{x_7}) = \prod_{l \in \bar{D}}(1- \hat{x}_l)
$$
が大きければ大きいほど予測が正確ということになります。
以上をまとめると、Skip-gram with Negative Sampling (SGNS)の評価関数は以下のようになります。
$$
\prod_{k \in D} \hat{x}_k ×\prod_{l \in \bar{D}}(1- \hat{x}_l)
$$
これが大きければ大きいほど予測が正確ということになります。積の形は微分の際に不都合が生じるので、対数をとって
$$
log(\prod_{k \in D} \hat{x}_k ×\prod_{l \in \bar{D}}(1- \hat{x}_l))\\
=\sum_{k \in D} log\hat{x}_k +\sum_{l \in \bar{D}}log(1- \hat{x}_l)
$$
そして、損失関数は「小さければ小さいほど予想が正確」になるものなので-1をかけて、
$$
Loss =-\sum_{k \in D} log\hat{x}_k -\sum_{l \in \bar{D}}log(1- \hat{x}_l)
$$
が損失関数になります。
最後にランダムな選び方です。
基本的には文書中の単語の頻度に基づいて選ばれます。頻度が高い単語は正解データとなる可能性があるので学習の中で大きくなりやすい傾向があります。そのため、もし正解データでない場合に小さくするように学習しておかないと大きくなり続けてしまいます。
そのため、頻度の高い単語ほど高い確率で選べれるように、逆に頻度の低い単語ほど低い確率で選ばれるようにすれば良いので、
単語$${w}$$が選ばれる確率を
$$
P(w) = \frac{文書中のwの出現数}{文書中の総単語数}
$$
とすれば良いことになります。注意点として、正解データの「その他」を選ぶ確率なので正解データを除く必要があります。これについては正解データ中の単語が登場したら再度選び直すなどで解決できます。
ここで「文書中に数回しか出てこないレアな単語が一切学習されなくなってしまう」という問題があります。その改良として、確率を$${\frac{3}{4}}$$乗したものを利用するというのがあります。 これによって極端に小さい数の確率を上げる一方で大きい数の確率はほとんど変えないことが出来ます。
$$
{0.9}^{\frac{3}{4}} = 0.92\\
{0.09}^{\frac{3}{4}} = 0.16\\
{0.01}^{\frac{3}{4}} = 0.032
$$
以上のように、確率が0.9のような大きな値については$${\frac{3}{4}}$$乗したところで0.92となるだけでほとんど変わりません。一方で、0.01のようにとても小さい確率は$${\frac{3}{4}}$$乗すると0.032と3倍程度まで確率が大きくなります。
この$${\frac{3}{4}}$$というのは度々使われる魔法の数字なので覚えておきましょう!
Word2vecの効率化2(hierarchical softmax)
negative sampling(ネガティブサンプリング)とは別の方法でWord2vecの計算量を減らすことを考えてみましょう。
softmax関数を別のもので代替して計算量を減らすという方向性は同じですが、やり方が異なります!
それが、階層的ソフトマックス(hierarchical softmax)を使った方法になります。具体例を見てみましょう👀
これまでの例と同様に"I like this pen."という文章について考えます。そしてnegative samplingの場合と同様にSkip-gramにおける効率化を例として考えます。

まず、今回単語の全体集合が8個であったとします。($${|V|=8}$$)つまり、今考えている5単語("I" "like" "this" "pen"".")以外に文書中にもう3単語あるとしています。
例えば下の図のように、"this"という単語が入力で与えられ、"this"の前後2単語を予測したい場合は"I" "like" "pen""."の4単語($${\hat{x}}$$の赤丸)の確率が高く、残りの"this"を含む4単語($${\hat{x}}$$の青丸)の確率が低ければ上手く予測できていることになります。
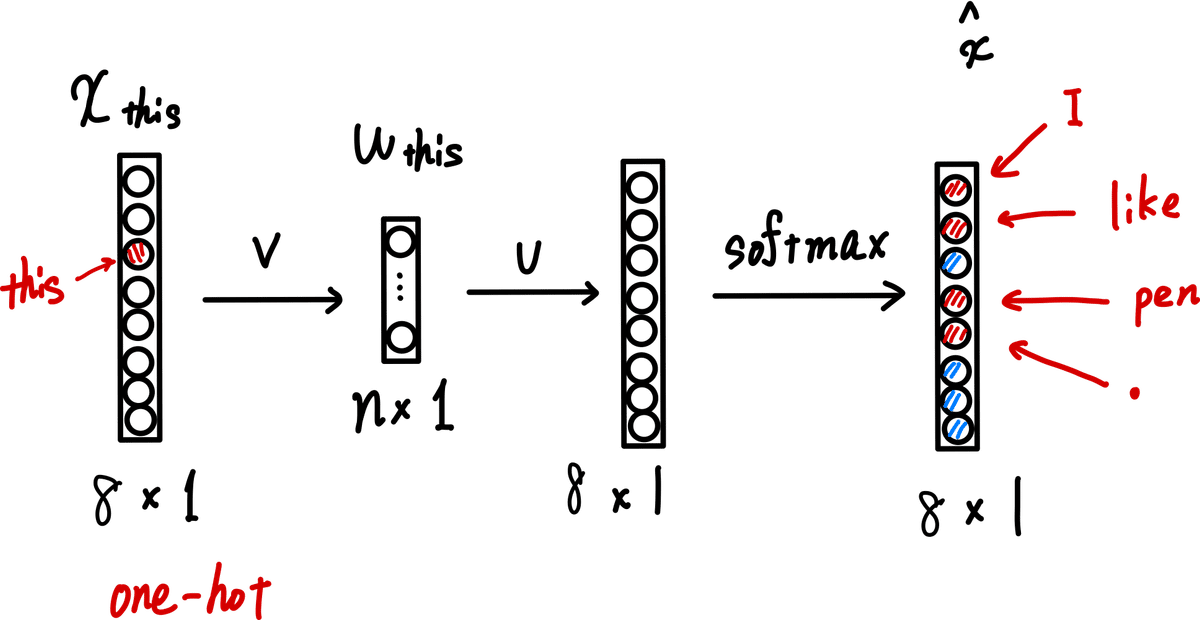
先の章でも説明したように、この際softmaxを計算すると8個分の指数関数を計算してその合計を求める必要があるのです。
しかし、実際は学習する時は"I""like""pen""."の4単語($${\hat{x}}$$の赤丸)の値が大きければ大きいほど良いだけなのでその他の4単語($${\hat{x}}$$の青丸)の分まで指数関数を計算するのは効率が悪いです。
(ここまでは前章のnegative samplingと同様の説明)
hierarchical softmaxではこの$${\hat{x}}$$の各値を求めるのに以下のような木構造が元になります。

かなりこれまでの話とは変わってくるので順番に噛み砕いて説明します。
まず計算方法です。それぞれの$${\hat{x}}$$の要素の求め方はそれぞれの葉に至るまでの枝に書かれている数字の積になります。
例えば、"this"が与えられたときの"I"の確率を表す$${\hat{x}_1}$$を求めたいときは、頂点から$${\hat{x}_1}$$の葉までのルートを以下のように考えます👇

そしてその全ての数の積を以下のようにとることで「"this"が与えられたときの"I"の確率」が求められます。
$$
\hat{x}_1=P(w_{I} | w_{this}) = 0.6 \times 0.3\times 0.2 = 0.036
$$
同様に、「"this"が与えられたときの"like"の確率」が以下のように求められます。

$$
\hat{x}_2=P(w_{like} | w_{this}) = 0.6 \times 0.3\times 0.8 = 0.144
$$
それぞれの計算方法は分かりましたか?ポイントは「頂点から対応する葉までのルートをとり、それらの積を取る」ということです。
このように木構造でsoftmaxを計算する仕組みを階層的ソフトマックス(hierarchical softmax)といいます。
これによって、通常のsoftmaxと違って全ての要素の指数関数を計算しなくても確率を計算することが出来て効率的です。
そしてhierarchical softmaxがsoftmaxとなるために重要な性質は一つのノード(図の丸)から出る枝上の数字の和が1になることです。具体的には以下のようになります。

逆にこれを満たさない以下のようなものは不適です。
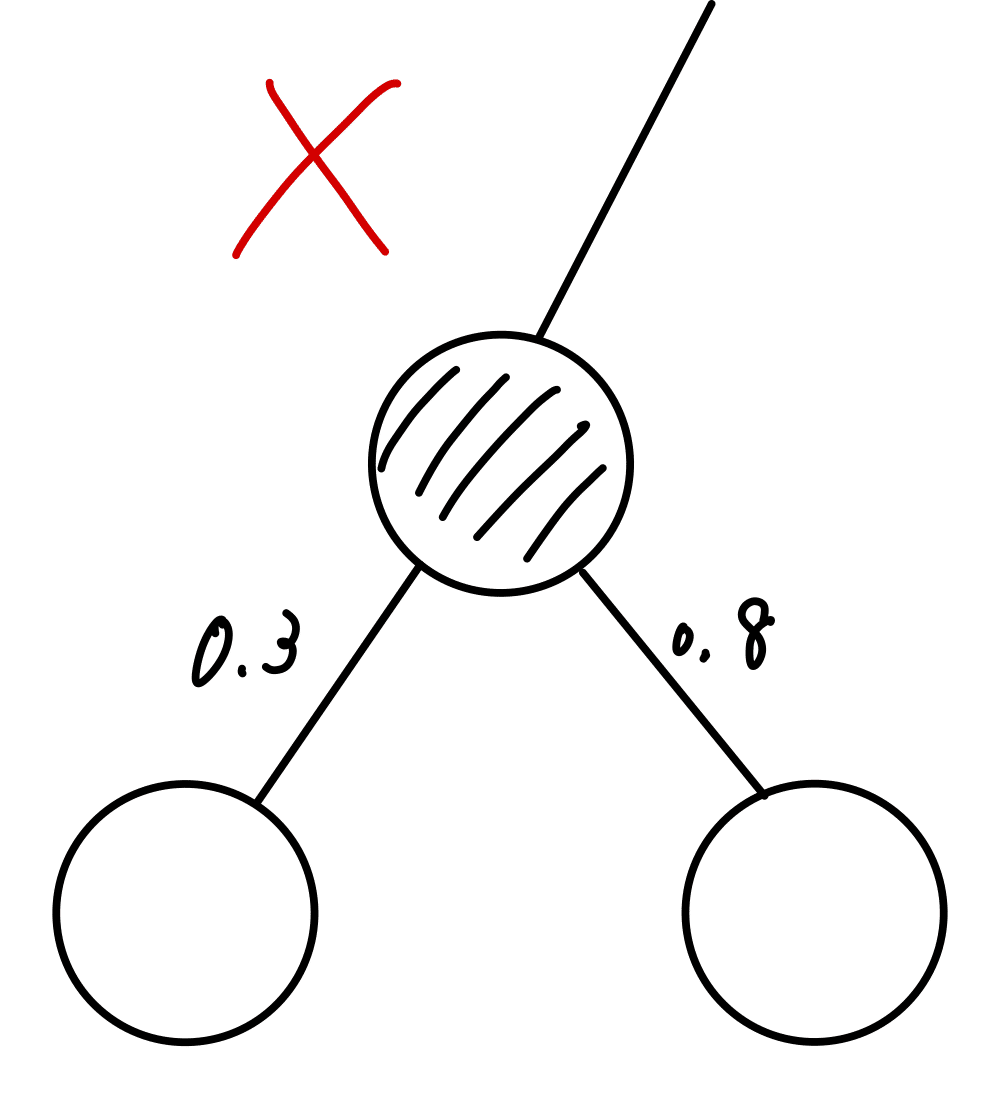
以上の性質によってsoftmaxの重要な性質である「要素の和が1」ということを実現できます。
$$
\hat{x_1} + \hat{x_2} + \cdots + \hat{x_8}
= 1
$$

次にこのhierarchical softmaxをskip-gramにどのように当てはめるかについて説明します。
これまでskip-gramで学習するのはUとVの行列の各要素でした。

その代わりにhierarchical softmax関数の各枝の値を学習します。

全体図は以下のようになります。

学習の例を1つ挙げて見ましょう。例えば、学習データが先ほどの例のように"I like this pen."であった時、損失関数
$$
L = -\sum_{k \in D} \hat{x_k}
$$
に基づいて以下のように調節します。
$$
u_{1} \leftarrow u_{1} - \alpha \frac{\partial L}{\partial u_1} \\
u_{2} \leftarrow u_{2} - \alpha \frac{\partial L}{\partial u_2} \\
\vdots \\
u_{7} \leftarrow u_{7} - \alpha \frac{\partial L}{\partial u_7} \\
$$
ただし、$${u_1,u_2,\cdots,u_7}$$は以下の通りです。

今回の例では"this"が与えられたときのhierarchical softmaxだけを挙げていますが、「"I"が与えられたときのhierarchical softmax」「"like"が与えられたときのhierarchical softmax」のように文書中の全ての単語についても同様に考えていくことになります。
まとめるとhierarchical softmaxは通常のsoftmaxを使ったものと比べて、
・確率の計算が高速
・U,Vの学習の代わりに木構造のそれぞれの枝を学習すること
が異なります。
chapter 1-5: Global Vectors for Word Representation (GloVe)とは
次に説明するword vectorの作成方法としてGlobal Vectors for Word Representation (GloVe)について説明します。
そのために、まず単語間の共起行列(word-word co-occurrence matrix)というものについて説明します。
単語間の共起行列(word-word co-occurrence matrix)
共起行列とはある単語が出現した時にその周囲の単語の出現回数を行列として表現したものになります。具体例を踏まえて考えて見ましょう。
例として以下の文書を考えます。
I like tennis.
I play the piano.
I like NLP.
この文書から作られた共起行列は以下のようになります。

気づいた人もいるかもしれませんが、これは前に扱ったWord-Document Matrixと同じです。もしこの行列の作り方が分からない方は再度確認して見てください。
共起行列のGlobal Vectors for Word Representation (GloVe)への適用
GloveはSkip-gramのモデルに改良を加えたものになります。まず、Skip-gramのアルゴリズムは以下のようなものでした。

そして、その時の損失関数は以下のようになりました👇
$$
L = -\sum_{k \in D} log\hat{x_k}
$$
(但し、正解データである"I","like","pen","."の添え字の集合をDとして、$${D = \{ 1,2,4,5 \}}$$)
これは"this"という単語の周りにおいて正解データが"I","like","pen","."である場合の学習になります。
これを発展させて、文書中のすべての単語について損失関数を考えたものをglobal cross-entropy loss(グローバルクロスエントロピー損失)といいます。具体的に見て見ましょう。👀
文書は以下のように与えられたとします。
I like tennis.
I play the piano.
I like NLP.
この場合、単語の種類は"I","like","tennis","play","the","piano","NLP","."の全8種類になります。
skip-gramではそれぞれの単語に着目して1つ1つ学習しました。
今回は説明を簡単にするためwindowサイズは1とします。
(「window sizeとは?」となった方は「Word-Document Matrix✖️特異値分解(SVD)」を見てください。)
例えば、文書の一単語目に当たる"I"からその直前後の単語"like"を推測するように学習します。(今回は"I"の直前には単語がないため"like"のみ)
これを"I"→"like"と書くことにします。
その次に"like"→"I","tennis",
"tennis"→"like","."
"."→"tennis"
"I"→"play"
"play"→"I""the"
$${ \vdots }$$
というように、文書中のすべての単語を1つ1つ順に学習しました。global cross-entropy loss(グローバルクロスエントロピー損失)はこれを一括に扱います。
先ほどの
"I"→"like"
"like"→"I","tennis",
"tennis"→"like","."
$${ \vdots }$$
のskip-gramにおけるそれぞれの損失関数を
$$
L_1=- \sum_{k \in D_1} log\hat{x_k}\\
L_2=- \sum_{k \in D_2} log\hat{x_k}\\
L_3=- \sum_{k \in D_3} log\hat{x_k}\\
\vdots
$$
とおくと、global cross-entropy lossは文書中の損失関数の合計をとります。
global cross-entropy lossをJとして
$$
J =L_1+L_2+\cdots\\
=-\sum_{i \in corpus} \sum_{k \in D_i} log\hat{x_k}
$$
ここでcorpusとは文書中のすべての単語のことを指します。
