MATLAB：sin関数のいろいろ

以前記事で弧度法の$${sin(\pi)}$$がゼロにならないって書きました。

MATLABではsin以外にもで度数法でsindと弧度法でも正確なsinpiがあります。
結果がこんな感じです。

たしかにsin以外はゼロになってます。便利そうですね。

sin関数の非ゼロ問題のアイデア

実はsin関数の非ゼロ問題って昔悩んだことがあって何か解決策ないか？ととりあえず考えたのが

1. 引数がpiの整数倍の時だけ強制的にy=0とする

2. yが限りなく0に近い時だけ強制的に０とする

こんな感じでしょうか？

x=[0:30:750]
%1の方法
m=mod(x,180)
y(m==0)=0
y(m~=0)=sin(x(m~=0)*pi/180)
plot(x,y)

%2の方法
yy=sin(x*pi/180)
y(abs(yy)<=10^-10)=0
y(abs(yy)>10^-10)=yy(abs(yy)>10^-10)
plot(x,y)

両者とも3行で書けて簡単です。結論言えば、”そこそこ正しいがあまり正確でない”と言ったところです。そしてゼロ検出という目的に関しては特に問題ないという程度です。

なぜなら簡単にグラフ書いたりする分にはせいぜい数周期分だけ考慮すればいいのですが、例えば”AM変調を扱う”とか”周期はゆっくりだが長い時間のシミュレーションしたい”という場合に問題になる可能性あります。

変数xがめちゃくちゃ大きいとどうなる？

そもそも誤差の原因が、sin関数とpiの誤差によるから当然なんですが・・・
sin関数で言えばちょっと極端ですが10^100piまでになると答えが-0.14とかかなり違いますね。
問題ですね。

そうするとsin関数の特徴として、

• -pi<x<piの範囲では正確

• $${-1\leqq sin(x)\leqq 1}$$で繰り返し

• $${sin(0.5\pi-x)=cos(x)}$$

というのを利用すると、$${x\pi}$$の範囲を4象限に場合分けして、三角関数をつなぎ合わせれば正確な解が得られそうな気がします。

結局sindとは

上記の問題を解決し度数法で扱える様にしたものが、実はsindです。
少なくともMATLABのR2008の時点では、実はファンクションmファイルで提供されていて、あえて記述はしませんが1で示した方法を改修して4象限ごとに場合分けした内容となっておりソースコードも見られました。

まとめ

MATLABで正確な三角関数を使うならsind,やsinpiを使いましょう。
そして、それは自分でも作れちゃったりする。

訂正

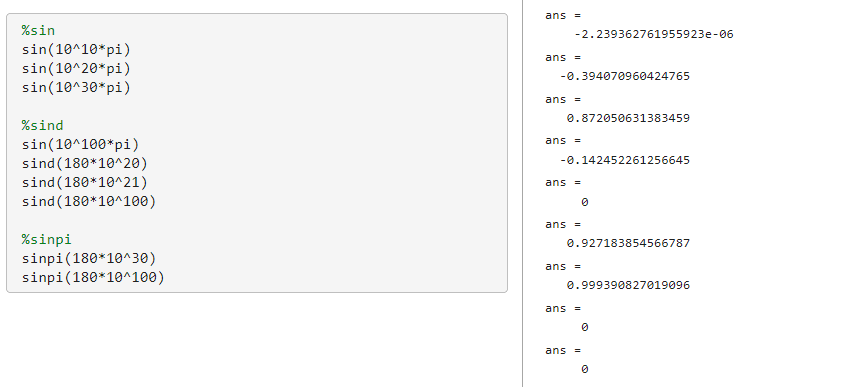
試しに再計算してみたところsinは10^20で大きな誤差が、sindは180*10^20までは正確っぽいけど180*10^21になると位相が90度変わった様な値になります。（アルゴリズムの特性上、誤差が発生すると90度分？）ですがsinpiは正確ですね。

私が使う範囲は頑張ってもせいぜい10^7周期位なんでゼロ検出以外の用途ではさほど問題ないんですがこういうの頭に入れて使った方が良いかもしれません。

ちなみに”こんな問題を解決したい！”とベンダーに相談すると回答としてはsinpi使ってくださいとなるかと思われます。そういった要望が増えると”将来廃止予定です。sinpi使ってください。”なってくと思いますよ。