
ファミコン全タイトルの傾向をTableauで分析してみた。(後編①:価格と容量の相関)
いきなりですが、↑↑↑の見出し画像、違和感ありますか?
よくよく見ると、指の数も手足の数も変だし、髪飾りもゆがんでるし、そもそも胴体もないんですが、妙にバランスが良く思えたので、そのまま使ってみました。
ここ数週間のAIの発達は凄まじいですね。来年には人類は絶滅しているんじゃないか、と思ってしまうほどです。
ですので、今のうちにTableauでファミコンの分析をやってしまいましょう。
あと、AIの事を「思考ルーチン」というのは、古すぎるのでやめましょう。
仮説のおさらい
前回「これを検証してみよう」と挙げた仮説をおさらいします。以下の4つでしたね。
①容量が大きいと石(ICチップ)の数が増えるため、価格が高くなっているのではないだろうか
②容量当たりの単価は年々安くなっているのではないか
③容量が大きいソフトは壮大なグラフィックや音楽が重要な「RPG」のジャンルが多いのではないだろうか
④発売日に傾向があるのではないか(クリスマスとか)
早速、前回Prepで整形したデーたをTableau Desktopで開いてみましょう。
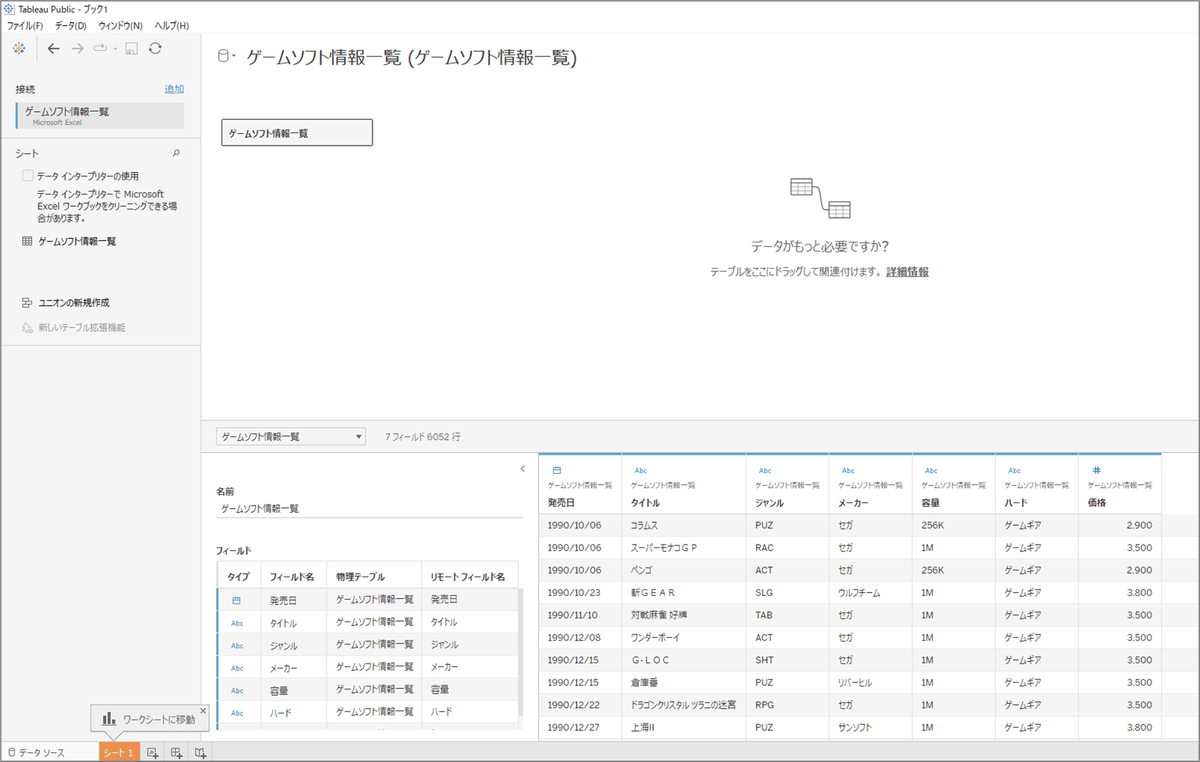
なんですが、ひとつ、気になるところがあります。

「容量」ですが、このままだとちょっと扱いづらいんですよね。
・「256K」「1M」のように、単位がそろっていない
・そもそも「文字列」になってしまっているので、計算ができない
なので、分析を始める前になんとかしたいです。
「単位をそろえる」「文字列を数字にする」なので、もしかするとExcelに一回入れてしまった方が楽な可能性はありますが、Tableauでも解決できます。

やってる事は簡単です。
・右から1文字目を確認して「K」だったら、「K」の文字を削除し「文字列から数字に変換」し、「1,000を掛ける」
・右から1文字目を確認して「M」だったら、「M」の文字を削除し「文字列から数字に変換」し、「1,000,000を掛ける」
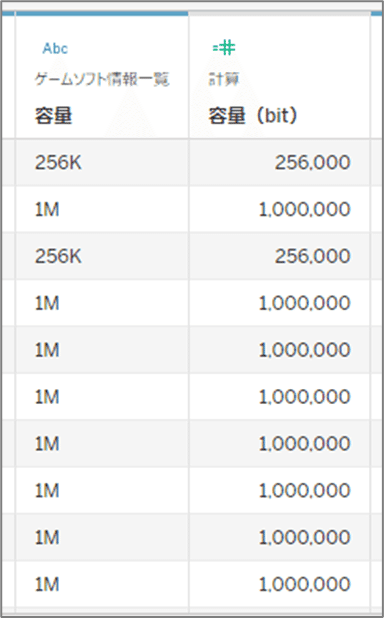
これで下準備は完了です。
いよいよ分析に入ります!
※便宜上、1,024ではなく1,000を掛けています。
仮説①:容量が大きいと価格が高い?
Playstationを初めてプレイした時、私を悩ました文字列がありました。

それまで、SFCなどのカセットメディアしか知らなかった私には、そもそも「ロード時間」という概念など存在していませんでした。
なので、ゲームを開始する前に、この画面でフリーズしたまま数十秒も待たされる事が、意味が解らなかったのです。
「え? これって『NO LOADING』の間違いで、エラーを起こしているわけじゃないよね?」
と本気で思いました。(そして何度もリセットボタンを押す)
サムライスピリッツなんか、1回の対戦をするのに、1分のロードが2回入った記憶があります…。対戦時間よりもロード時間の方が長い…。なんて時間の浪費…。
私はこの時初めて、カセットメディアのありがたさを身に染みて知ったのでした。
ただし。
カセットメディアは、その本体にICチップそのものを搭載しているため、CDメディアよりも、物理的な媒体価格が高かったのです。
容量を増やすには、
・石(ICチップ)の数を増やす
・石1つあたりの容量を増やす
しか手段がなく、どちらにしても価格が上がる要因でした。

が、石の数が必ずしも多かった(大容量)訳でもないようです…。

セーブ式のカセットにはコイン電池が入っていました。
電池切れしたらセーブできないので要交換。
では、
容量と価格の相関
を見ていきましょう。

一応、確認しておきましょう。
今回は「容量が価格に与える影響」を調べたいので、
目的変数:価格
説明変数:容量
です。
従って、目的変数の「価格」が縦軸になっていればOKです。
この状態ではまだちょっと見づらいのですが、特徴的なサンプルがありますね。
・「容量が少ないのに、やたらと価格が高い」グラフの左上の外れ値
・「容量が大きいのに、価格が安い」グラフ右下の外れ値
一応、調べておきましょう。

あとで除外しておきましょう。
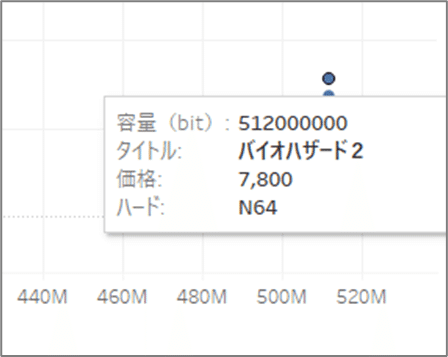
外れ値についてなんとなくわかりましたが「容量」の表示が「512,000,000」となっていて、ちょっとわかりづらいですね。
折角なので、全ての単位を「Mビット」で合わせておきましょう。
Tableauは、↓↓↓のように直接式を打ち込んでしまうことができます。



さて。
では、ここでもう一つ仮説を立てたいと思います。
というのも、↑↑↑で見た通り、Nintendo64では大容量のソフトがありますが、ファミコンではそうもいかず、ファミコンとNintendo64を同時に比較しても傾向がつかめない可能性があるからです。
仮説:容量と価格の相関は、ハードウェアごとに異なるのではないだろうか
先ほどの散布図において「ハード」ごとに色分けしてみます。

という訳で、今回は「ハードごとに相関を確認」していきたいと思います。
まずは
ファミコン

いいですね。
決定係数(R2乗)が0.36もありますので、相関係数(R)は0.6ほどあります。これは中~強程度の相関があるとみていいでしょう。
つまり、ファミコンにおいては
「容量が大きい方が価格が高い」が成立
しています。
せっかくなので、外れ値も見てみましょう。
容量が小さいのに、15,000円くらいしてるサンプルがありますね…。
なんじゃこりゃ?


これはあれですよ。
ファミコンにキーボードつないで、MSXみたいにBASICプログラムできるようにするやつですよ。
そりゃあ、高い訳だ。
じゃあ、容量が一番大きいサンプルは?
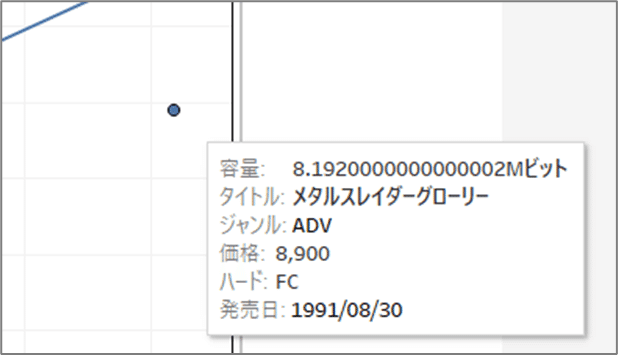

このソフト、ファミコンなのに8Mビット(1Mバイト)もあるんですよね。
グラフィックが特徴的なゲームは「エメラルドドラゴン」とか色々ありますが、メタルスレイダーグローリーはSFC版が出るほど「ファミコンとしてはグラフィックに凝った」作品でした。

スーパーファミコン

ファミコンほど顕著に相関が出ていないな、と思ったら、とんでもない外れ値がいました。

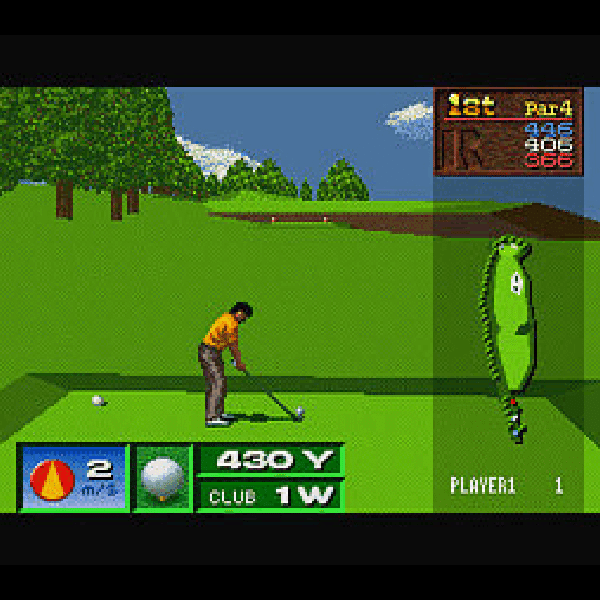
ゴルフゲームと言えば「ジャンボ尾崎のホールインワン」「遥かなるオーガスタ」などが有名だし、ポリゴンを使ったSFCのゴルフゲームなら「デビルズコース」がありますが、このゲームはノーマークでした…。
あと気になったのが「0Mビット」のサンプル。
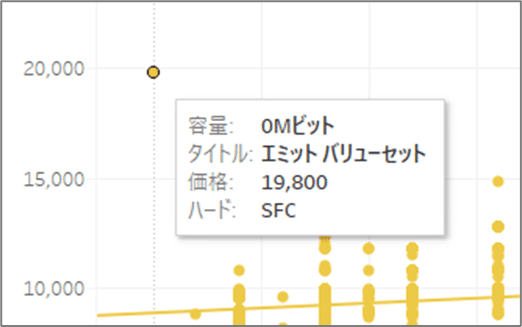


まさか、このソフトだとは思いませんでした。
これ、
英語学習ソフト
なんですよ!
脚本が赤川次郎、キャラクターデザインがいのまたむつみ、そして音楽が小室哲哉という豪華キャストでした。
なぜ「0Mビット」なのかわかりませんが、情報がなかったか、公開してなかったんでしょうね。

外れ値を除いた決定係数は0.036。相関係数で0.19ほどですので「相関はほとんどない」とみてよさそうです。
これは仮説ですが、
・SFCの時代になると石の価格が安く大容量になってきたので、容量よりも中身で勝負するようになった
・SFC後期に、任天堂がライセンスフィーを下げたため、安くソフトを売れるようになった
あたりが、相関が思ったほど出なかった要因かと思われます。
因みに「48Mビット」もある作品は「テイルズ オブ ファンタジア」と「トラバース」でした。
「テイルズ」は、SFCとしては「しゃべりまくる」上に「歌つきの主題歌が流れる」演出がありましたので、納得です。SFCで歌って…。
「FF6」のオペラシーンはSFCで登場した「歌」ですが、ちゃんと言葉になっていません。
「ヘラクレスの栄光4」の子供の歌は、かなりよく歌えていますが、それでも「テイルズ」ほどではありませんね。
「トラバース」はクオータビューのRPGですね。当時、流行ったんです。クオータビュー。「ボンバザル」「カービーボウル」「レディーストーカー」「エナジーブレイカー」「タクティクスオウガ」など、思い出せるだけでも沢山ありますね。
あれ? 48Mビットってこの2作品だけでしたっけ?
「ルドラの秘宝」「トレジャーハンター」「バハムートラグーン」「ミスティックアーク」あたりって48Mなかったでしたっけ?
ゲームボーイ

ゲームボーイです。
これまた、すごい外れ値が2つ…。
見ていきましょう。
1つは、↑↑↑の画像の通り「電車でGO2」です。
え!? GBで64Mビット(8Mバイト)!?
そんなに、あの小さなカセットに詰め込めたの??
知りませんでした。





外れ値を除いた決定係数は0.125。相関係数は0.35なので「弱い正の相関がある」と言ってしまってよいと思います。
ゲームボーイは、他にもカメラを搭載できたり、プリンタを搭載できたりと、とにかく色々なハードウェアオプションが登場した、挑戦的なハードでした。
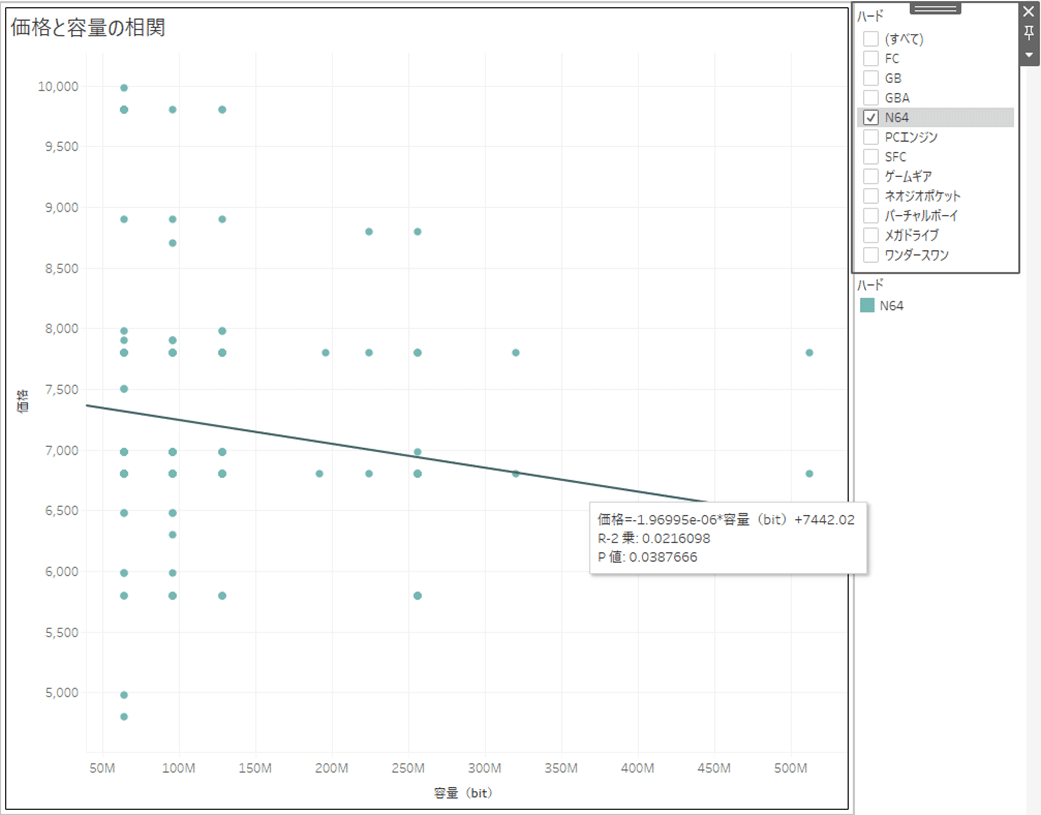
Nintendo64
Nintendo64は、開発段階では「ウルトラ64」というコードネームでした。確か、開発リリース当初は「ヘッドマウントディスプレイで電車の中でもプレイできる」ものすごくSFチックなハードとして扱われていた記憶があります。
が、フタを開ければ「ヘッドマウントディスプレイ」は「バーチャルボーイ」として「据え置き型のヘッドマウント」となり、Nintendo64は単純なカセットタイプの据え置き機として登場しました。
バーチャルボーイはバーチャルボーイで未来を感じましたけどね…。真っ赤な画面、立体視できることから上下レイヤー概念のあるゲームたち。
決定係数が0.021。回帰係数がマイナス値なので、相関係数は-0.14ほどです。「ほとんど相関はない」と言ってよさそうですが、マイナス値というのが面白いですね。
Nintendo64くらいになると、かなり大容量のチップを搭載できるようになったうえ、Playstationやセガサターンといった競合ハードウェアとの競争の上、価格競争などがあった事が想定できるかと思います。

いかがでしたでしょうか
スミマセン、本当は後編で仮説4まで行く予定だったんですが、仮説1だけでこれだけのボリュームになってしまいました;^^
ので、後編自体を複数回に分けます。
次回、後編②をお楽しみに!
※当記事に書かれた内容は、全て著者の解釈によるものであり、公式の見解を代弁するものではありません。
