見出し画像

Pythonでネスレの株価を予測

taron

はじめに

メディア関係の仕事をしています。仕事の幅を広げたいと思い、Pythonによるデータ分析について勉強を始めました。その最初のアウトプットとして取り組んだのが、この記事です。

目次

１、この記事の概要と目的
２、コードの解説
４、考察
５、今後の課題と感想

１、この記事の概要と目的

Pythonで時系列分析を行い、SARIMAモデルによる株価予測をやってみることにしました。時系列分析とは、時間経過とともに変化するデータを分析する手法のこと。そして、SARIMAモデルは、季節によってパターンが変わるものを予測したり、過去のデータから未来の動きを予測したりすることができる有名なツールです。「このSARIMAモデルを使って、株価を予想してみよう」というのが、この記事の目的です。株価を予測する対象には、世界最大の食品飲料企業であるネスレを選びました。

注意点: 本記事では、株価予測を簡略化して扱っており、実際の投資には利用できません。株価は様々な要因によって変動するため、より精度の高い予測には、経済指標や企業情報など、多岐にわたるデータ分析が必要です。

＜実行環境＞

  • Windows PC

  • Google Collaboratory

  • Python

２、コードの解説

＜作業手順＞

  1. 株価データの取得

  2. 日付け範囲の作成

  3. 時系列データを日単位に集約する

  4. 欠損値の確認

  5. 時系列データを分解する

  6. 定常性の確認

  7. SARIMAモデルの最適なパラメータを見つける

  8. SARIMAモデルによる株価予測


１、株価データの取得

まずは必要なライブラリを取得します。Yahoo!ファイナンスからは、ネスレ（NESN.SW）の2010年1月1日～2023年12月31日の株価データをダウンロードし、PandasのDataFrame形式で取り出します。その後、そのDataFrameから「終値」のデータのみを抽出します。

import yfinance as yf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.tsa.seasonal import seasonal_decompose
import datetime
import itertools
ticker = 'NESN.SW'
df = yf.download(ticker, start="2010-01-01", end="2023-12-31", interval="1d")
df

２、日付け範囲の作成

次に、2010年1月1日から2023年12月31日までの日付を１日の間隔で生成し、それをindexという変数に格納します。上記のdfのrows（列）は3521ですが、下記のコードを実行すると、2010-01-01～2023-12-31の日数は実際には5113であることがわかります。つまり、株価の数値がない日があり、これを放置したままだと正確な予測ができません。当初は、下記のコードを省略したため、最終的な予測グラフを出力した際にエラーが発生しました。

index = pd.date_range('2010-01-01', '2023-12-31', freq='d')
index

３、時系列データを日単位に集約する

各日ごとに、数値型の列の平均値を計算し、新しいデータフレームを作成します。これによって、株価の数値がない日を見つけることができます。

#1ヶ月毎のデータに変更しシンプルにする
df = df.resample(rule = "M").mean()
#グラフにして可視化
plt.plot(df["Close"])
plt.show()

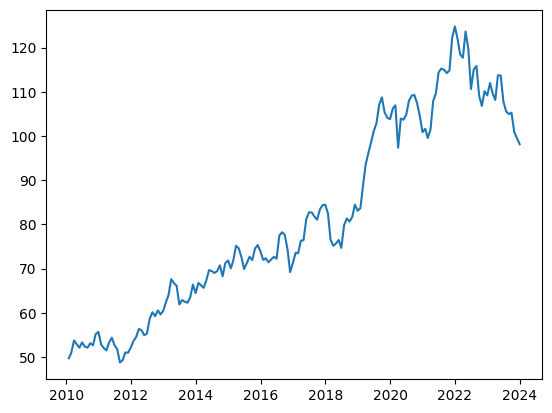
４、欠損値の確認

データ分析を行う上で、データの中に抜けている部分が含まれていると、分析結果に誤りが生じたり、モデルの精度が低下したりする可能性があります。下記のコードは、PandasのDataFrameであるdfに対して、各列の欠損値の数を数えて表示するものです。実行すると欠損値が1587か所あることがわかります。

#欠損値の確認
df.isnull().sum()
	0
Open	0
High	0
Low	0
Close	0
Adj Close	0
Volume	0

dtype: int64

５、時系列データを分解する

時系列データをトレンド、季節性、残差という3つの要素に分解します。データの動きを、この３つの要素に分解することで、データの特性をより深く理解できます。例えば、株価の変動が、長期的な経済成長によるトレンドと、季節的なイベントによる影響を受けているのかを分析できます。

sm.tsa.seasonal_decompose(df["Close"], period=12).plot()
plt.show()

６、定常性の確認

定常性とは、その統計的な性質（平均、分散、自己共分散など）が時間経過とともに変化しないことを意味します。つまり、データの分布が常に一定であるということです。下記のコードでは、Pythonのライブラリを使ってADF検定を行っています。dfという変数に時系列データが入っており、adfuller関数で検定を実行しています。ADF検定は、データが定常であるかどうかを調べるための統計的な手法です。p値が小さいほど、データは定常であるという証拠が強くなります。

# 定常性の確認（Augmented Dickey-Fuller test）
from statsmodels.tsa.stattools import adfuller

# df["Close"]で終値の列を指定
result = adfuller(df["Close"]) 

print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])
print('Critical Values:')
for key, value in result[4].items():
    print('\t%s: %.3f' % (key, value))
ADF Statistic: -1.084308
p-value: 0.721289
Critical Values:
	1%: -3.471
	5%: -2.879
	10%: -2.576

p値が0.05より大きい場合: データは非定常である可能性が高いと判断できます。よって現状では、定常性がない可能性が高いとの結論になりました。

７、SARIMAモデルの最適なパラメータを見つける

PythonでSARIMAモデルのパラメータを自動でピッタリの値にする機能はありません。そのため、BICという機能を使って最適なパラメータを見つけ出すプログラムを作る必要があります。BICは、値が小さいほどパラメータの設定が優れていることを表します。

def selectparameter(DATA,s):
    p = d = q = range(0, 2)
    pdq = list(itertools.product(p, d, q))
    seasonal_pdq = [(x[0], x[1], x[2], s) for x in list(itertools.product(p, d, q))]
    parameters = []
    BICs = np.array([])
    for param in pdq:
        for param_seasonal in seasonal_pdq:
            try:
                mod = sm.tsa.statespace.SARIMAX(DATA,
                                                order=param,
                                                seasonal_order=param_seasonal)
                results = mod.fit()
                parameters.append([param, param_seasonal, results.bic])
                BICs = np.append(BICs, results.bic)
            except:
                continue
    return parameters[np.argmin(BICs)]

selectparameter(df["Close"],12)
[(0, 1, 0), (0, 1, 1, 12), 775.0672208083015]

８、SARIMAモデルによる株価予測

BICによって最適なパラメータがわかったので、SARIMAモデルを構築し、将来の株価を予測します。予測結果を可視化し、モデルの精度を評価します。

#モデルの構築
SARIMA_NESN = sm.tsa.statespace.SARIMAX(df["Close"],order=(0, 1, 0),seasonal_order=(0, 1, 1, 12)).fit()

#predに予測データを代入
pred = SARIMA_NESN.predict('2022-1', '2025-12')

#predと元の時系列データを可視化
#予測データは赤色で表示
plt.plot(df["Close"])
plt.plot(pred, "r")
plt.show()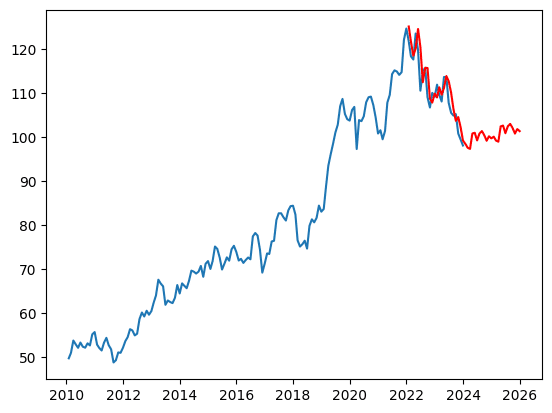
ネスレの株価の実績値（青）と予測値（赤）

３、考察

2022年以降は下降傾向だったが、24年頃からは横ばい、あるいは上昇傾向に転じるとの予測が得られた。

４、今後の課題と感想

本記事では、SARIMAモデルを用いたシンプルな株価予測を行いました。より精度の高い予測を行うためには、以下の点が課題として挙げられます。

  • 特徴量エンジニアリング: 株価に影響を与える他の経済指標や企業情報を追加し、より多くの特徴量を用いたモデルを構築する。

  • モデルの比較: SARIMAモデルだけでなく、他の時系列分析モデル（LSTMなど）との比較を行い、より適したモデルを選択する。

  • 予測精度の評価: RMSEやMAEなどの評価指標を用いて、予測精度の定量的な評価を行う。

今回はPythonを用いてSARIMAモデルによる株価予測を行ってみました。まだまだ理解が及ばない点が多いけれど、何とか形にできたことでスタートに立てた気がします。これからも学習を続けていき、様々なデータ分析ができるようになりたいと思いました。

いいなと思ったら応援しよう！

この記事が参加している募集

#勉強記録

15,896件