「建設・不動産のデジタル化　〜FMBIMの活⽤〜」：その17　【コラム２】 ニューラルネットワークの原理

①情報ネットワークモデル

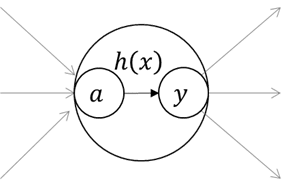
　情報ネットワークは文字通り入力された情報を出力へ流す仕組みのことをいう。図―１はx1,x2に情報が入力され→をたどってｙへ出力される流れを示した図である。途中のｗは重み値といい、ｓは流れてきた情報の仕分けをする部分だ。情報を流す仕方は次の式を通して下流へ送る。

図 74　情報ネットワーク

図 75　重み値とバイアス

x1、x2から入ってきた値は重み値を掛け合わされｙの値になる。この値がプラスの場合ｙ＝１、マイナスの場合ｙ＝０になる。この変換をするのがh(x)という関数である。この関数を活性化関数という。式で書くと(3)式になる。

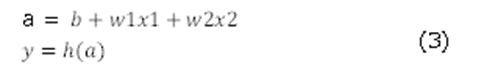
h(x)が（2）か（3）かの違いでパーセプトロンかニューラルネットワークかの違いになる。
つまり、yの値が０，１で出力されるか、０~１の間の実数で出力されるかの違いである。
式(2)はステップ関数、一方(4)はシグモイド関数と呼ぶ。
ここで、ｂの役目は関数全体の位置を決める値である。入力値に重みを掛けそれらをプラスしバイアスをプラスして式全体の値が決まる。これが情報ネットワークの基本原理である。

図 76　活性化関数

②ニューラルネットワークの仕組み

情報ネットワークの原理が分かったところで、実際に入力情報がどのように判断されどのように答えにたどり着くか述べてみる。
図は4層構造の情報ネットワークの図である。列には1層、2層という名称がついている。図では3層が出力層と呼ばれる層で、入力された情報の特性に応じた値が出てくる。

図 77　実際のネットワーク

図を式で記述すると式（５‘）となる。これをベクトル形式で書き表すと、式(5)になる。ニューラルネットワークは行列の計算として表すことができる。この式を詳しく図示すると図－5になる。

図 78　ニューロンネットワークの中の計算

ニューラルネットワークを構成している〇はニューロンと呼ばれ、ニューロンを構成している〇をノードという。
図では黒い矢印で表した流れが計算の流れであるが、ニュウラルネットワークではすべての入力値に対して同じ流れで計算される。
•       入力値は重みを掛け合わされ、次の層のニューロンへ伝えられる。
•       入力値は全てのニューロンへ伝えられる。
•       各層のニューロンでは前層の値はSigmoid関数に入力され次のニューロンへ流される。Sigmoid関数の特徴を生かして必要情報とそうでない情報をふるいにかける。入力情報がマイナスの大きな値ではSigmoid関数の出力は０に近いので、層を伝わる間に消えてしまう。

図 79　ニューロンとノード

③　出力関数について

入力値が層を伝わりながら、出力層に到達する。ニューラルネットワークの出力にはソフトマックス関数を使う。

ソフトマックス関数は分類に使われる出力関数である。

役割は流れてきた情報を目的に合致した値として誘導する役割がある。ソフトマックス関数は各最終層から流れてきた値に対して全体の割合で表示する関数である。

ソフトマックス関数は 指数関数を使い（eはネイピア数）、その値はニューロンの数がn個であり、そのｋ番目が (6)式で表される。

図は最終層から出力層へ情報が伝わり、出力層の値がy1、y2で算出される。

出力層のニューロンの数は解く問題に応じて適宜決められる。本文の工事名称の分類が4種類なら出力層のニューロンの数は４つになる。

図 80　Sigmoid関数の形状

図 81　最終層と出力層

④　損失関数

損失関数はニューラルネットワークの精度を判定する機能を持つ。

一般的に使われる損失関数は2乗和誤差と交差エントロピー誤差である。

分類問題で使われるのは交差エントロピー誤差、式(7)で表される。

図のグラフは交差エントロピー誤差を示し、横軸がykを縦軸がEを表す。

交差エントロピー誤差はykが1に近くなればEは0に近づく。入力の値が特定の出力に確定する割合を数字で表す。

あｓｄｆｓ

図 82　交差エントロピー誤差

入力された値はたくさんの重みで変換されながら出力層にたどり着く。たどり着いた値は交差エントロピー誤差により、ニューラルネットワークの性能を評価されることになる。途中の重み値を少し変化させると、出力値も変化する。
その変化が１から離れるなら、反対へ変化させればよい。各重みを少しずつ変化し、出力の交差エントロピー誤差をできるだけ０に近づけるように重みを調整する。
つまり、交差エントロピー誤差を最小にするようにたくさんの重みを調整して重み値を決めることが、入力値が特定の出力値に至る経路を決めることになる。
図のグラフの赤破線は左図の出力層の第3項目を交差エントロピーで表示した。
ニューラルネットワークではラベルt3＝１、y3=0.6　ゆえにE=0.51である。
図ではy3=0.1の場合はE=2.3で右のグラフの黒破線になる。ニュウラルネットワークの精度が良ければ、出力値は“０”に近づくことになる。
ニューラルネットワークの原理はそれほど難しくはないが、ニューロンの数が数百万という数に上るので、計算が遅くなる。この演算のスピードを速めるために、ソフト的にもハード的にも様なざま工夫がされている。

図 83　交差エントロピー誤差によりニューラルネットワークの 精度を比較する