【解説】高専🏫 5年間分の数学📐を高専卒が解説してみた👨🏫
みなさんこんにちは！
高専プロモーションチャンネル
【たにに】でございます。
今回は
高専🏫に入ってから
一体どういった数学📐を学ぶのか
これについてご紹介したいと思います。
高専に入って何故 数学📐を学ぶか✏️というと
工学⚙に数学📐の知識📚を応用するために
数学📐の勉強✏️を行います✎
どんなところで
応用が利くのかを解説👨🏫しながら
ご説明します📚
主には中３～新高専1年生向けです🌸
それでは行ってみましょう💨💨
YouTubeチャンネルでも
動画で説明していますので是非ご覧ください！
①1～2年生(新基礎数学🟦位)
1: 整式の計算・方程式・不等式 P(x) ≧ < =
2: 関数とグラフ・種々の関数(べき・分数・無理・逆) f(x) f/g/h
3: 指数関数・対数関数 📈📉
4: 三角関数 sin cos tan
5: 点と直線・2次曲線・場合の数と数列 💹 🎲
1～2年(進度が速い高専では1年生)で学ぶ数学🟦は
このような内容となっております✨
[[CM]] 大日本図書 新基礎数学 [完全 解説書]
高専数学の勉強が楽になります✨
詳しい解説書📚で、いい点数をたくさんとろう！
【工学のどこに生きてくるのか】
1～2年生の間では
工学の応用/道具🛠として
数学の基礎知識📚を学びます
大体の高専では
この青の囲いを1つの単元
【解析学📊】として
学ぶところが多いと思います🏫
例えば
"システムによって得られた波形を
解析したり、どういう風に扱ったりするのか"
などに使える初歩的な単元・領域に
なっていると思います。
②2～3年生（新線形代数🟧）
平面ベクトル■
空間ベクトル📦
行列・行列式（とその応用）(3 3 4) |A|
2～3年で学ぶ線形代数🟧は
このような内容となっております✨
【工学のどこに生きてくるのか】
1.連立一次方程式が高速で解けるようになる
今までは手計算だったものが
コンピューターに切り替えることで
高速で答えることができるようになります💻
2.2次元以降の次元を1次元で記述可能に
複雑で難しいものを
簡単に記述できる🖋ようになります。
3.回転や反転がメッチャ簡単に書ける
画像の加工アプリ📱のように
ボタン🕹一つで画像🖼が回転や反転できると思いますが
これはまさに線形代数🟧の知識が使われています👀
高専の専門の話に直結するような数学の概念🟧と
なっているのが線形代数🟧です。
④データ解析📊の応用
1～2年生の頃に学んで行くデータ解析。
コチラにも線形代数🟧は応用が利きます。
微分積分学と並んでとても重要な
学問の領域になっていますので
ここは必ず頑張っておきたいところですね💪
③2～4年(新微分積分I / II 🟩)
【Ⅰ(2-3年生)】 【Ⅱ(3-4年生の内容)】
・微分 ・偏微分
・微分の応用 ・重積分
・積分 ・微分方程式
・積分の応用 ・関数の展開
【工学のどこに生きてくるのか】
①加速度測定器
警察がネズミ捕りなどの際に使用している
加速度測定器🚓🟥
コチラには微分の概念が
施されています。
②システムの出力形式の解析
音楽などを録音・編集したことはありますか？
音は波形で表示されますが
この波形を解析するのは
積分の知識が必要になります👀
③面積や体積がわかる(複雑な図形でも)
こちらでも
計算する際には積分や偏微分の知識が
使われています✏️✏️
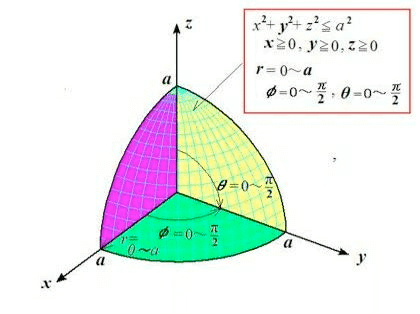
これも情報工学・土木・建築には
必ず必要になってくると言えるでしょう。
特に力を入れて頑張っていきましょう✨✨
まとめ
数学の勉強は大変ですよね💦
ですが今あなたが行っている勉強は
どんなことに応用されているから
学ぶ必要があると理解する💡💡
これを意識するだけで
より頭に入ってきますし
将来必ず役に立つスキルとなります。
どんなところで
実際に使われているのかを
意識して日々頑張っていきましょう💪
閲覧ありがとうございました！
それではまた。
【高専チャンネル【公式】 高専入試・受験・大学編入】
【高専に関するメディア,まとめとリンク】
↑クリックすると色々なところへ行けます↑
【【解説】高専5年間分の数学を高専卒が解説してみた】
この記事が気に入ったらサポートをしてみませんか？