代数幾何入門

§0. はじめに

この記事は随時更新します。

環、位相空間についての基本的な知識は仮定する。

可換環$${R}$$は単位元を持つとする。
環の準同型は単位元を単位元に移すものとする。すなわち、$${R, S}$$を可換環、$${1_R, 1_S}$$をそれぞれの単位元、$${f \colon R \to S}$$を環の準同型としたとき、$${f(1_R) = 1_S}$$を満たす。
また$${R}$$加群は単位的であるとする。すなわち、$${R}$$を可換環、$${1_R}$$をその単位元、$${M}$$を$${R}$$加群としたとき、任意の$${m \in M}$$に対し$${1_R m = m}$$を満たす。

$${\mathbb{Z}, \mathbb{Q}, \mathbb{R}, \mathbb{C}}$$はそれぞれ整数、有理数、実数、複素数全体の集合を表す。

環$${R}$$上の多項式環を$${R[T]}$$と書く。$${R[t]}$$のように小文字で書いた場合は、$${R\subset S}$$を満たす$${S}$$の元$${t}$$を$${R}$$に添加した環を表し、$${t}$$は$${R}$$上の不定元とは限らない。

§1.素スペクトル

§1.1. 素スペクトル

定義1.1.1. 素スペクトル
可換環$${R}$$の素イデアル全体の集合を$${\mathrm{Spec}\ R}$$と表し、$${R}$$の素スペクトルという。

例1.1.2. $${\mathbb{Z}}$$の場合
$${\mathrm{Spec}\ \mathbb{Z} = \{ (0), (2), (3), (5), \ldots \}}$$である。
$${(0)}$$以外は素数と1対1に対応する。

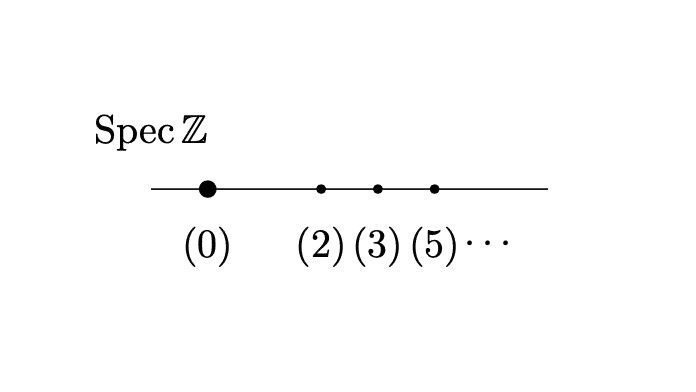
よく教科書などでは上の図を見かけるが、個人的には以下の図をおすすめする。違いは$${(0)}$$が点ではなく、$${(2), (3), (5), \ldots}$$を通る（直）線になっていることである。これは古典的な代数幾何との対応や、次節で考える$${\mathrm{Spec}\ R}$$の位相が理由である。

例1.1.3 $${\mathbb{C}[T]}$$の場合
$${\mathrm{Spec}\ \mathbb{C}[T] = \{ (0) \} \cup \{ (T-a) \mid a \in \mathbb{C} \}}$$である。
$${\{ (T-a) \mid a \in \mathbb{C} \}}$$は$${\mathbb{C}}$$と1対1に対応する。

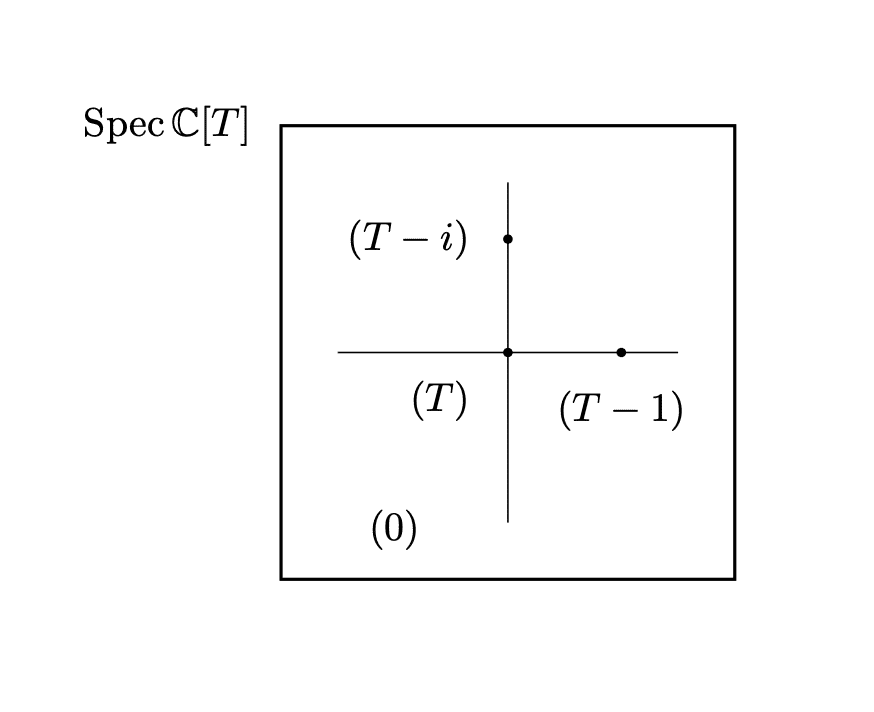
$${\mathrm{Spec}\ \mathbb{C}[T]}$$において$${(0)}$$は平面全体である。また、複素数平面と対応させるために平面で書いているが、代数幾何的には1次元である。

演習1.1.4
$${\mathrm{Spec}\ \mathbb{C}[T] = \{ (0) \}\cup\{ (T-a) \mid a \in \mathbb{C} \}}$$
を証明せよ。

証明
$${\mathbb{C}[T]}$$は単項イデアル整域であるから、$${(0)}$$以外の素イデアル$${\mathfrak{p}}$$は既約元$${f\in\mathbb{C}[T]}$$を用いて$${\mathfrak{p} = (f)}$$と表せる。
$${\mathbb{C}}$$は代数閉体であるから$${f = c(T-a)\ (a \in \mathbb{C})}$$と表せ、$${(f) = (T-a)}$$である。
逆に、これらは全て素イデアルである。

例1.1.5. $${\mathbb{R}[T]}$$の場合
$${\mathrm{Spec}\ \mathbb{R}[T] = \{ (0) \} \cup \{ (T-a) \mid a \in \mathbb{R} \} \cup \{ (T^2+aT+b) \mid a, b \in \mathbb{R}, \text{$T^2+aT+b$は既約多項式} \}}$$である。
$${\{ (T-a) \mid a \in \mathbb{R} \}}$$は$${\mathbb{R}}$$と1対1に対応する。
$${\{ (T^2+aT+b) \mid a, b \in \mathbb{R}, \text{$T^2+aT+b$は既約多項式} \}}$$は$${\mathbb{C} \setminus \mathbb{R}}$$と（多項式とその根の2つという対応で）1対2で対応する。

演習1.1.6.
$${\mathrm{Spec}\ \mathbb{R}[T] = \{ (0) \} \cup \{ (T-a) \mid a \in \mathbb{R} \} \cup \{ (T^2+aT+b) \mid a, b \in \mathbb{R}, \text{$T^2+aT+b$は既約多項式} \}}$$
を証明せよ。

証明
$${(0)}$$以外の素イデアル$${\mathfrak{p}}$$が既約元$${f}$$を用いて$${\mathfrak{p} = (f)}$$と表せることは$${\mathrm{Spec}\ \mathbb{C}[T]}$$の時と同じ。
$${f}$$は$${\mathbb{C}}$$において共役な根を持つから、$${f = c(T-a)\ (a \in \mathbb{R})}$$または$${f = c(T-z)(T-\overline{z})\ (z \in \mathbb{C} \setminus \mathbb{R})}$$と表せる。
このとき、$${(f) = (T-a)}$$または$${(f)=(c(T-z)(T-\overline{z}))=(T^2+aT+b)}$$, ($${T^2+aT+b}$$は既約多項式)である。
逆に、これらは全て素イデアルである。

例1.1.7. $${\mathbb{Z}[T]}$$の場合
$${\mathfrak{p}}$$を$${\mathbb{Z}[T]}$$の素イデアルとする。
$${\mathfrak{p} \cap \mathbb{Z}}$$は$${\mathbb{Z}}$$の素イデアルなので$${(0), (p)}$$（$${p}$$は素数）のいずれかである。
$${\mathfrak{p} \cap \mathbb{Z} = (0)}$$を満たす素イデアル$${\mathfrak{p}}$$は$${\mathbb{Z} \setminus \{ 0 \}}$$による局所化$${\mathbb{Q}[T]}$$の素イデアルと1対1に対応する。
$${\mathfrak{p} \cap \mathbb{Z} = (p)}$$を満たす素イデアル$${\mathfrak{p}}$$は$${p\mathbb{Z}[T]}$$による剰余環$${\mathbb{F}_p[T]}$$の素イデアルと1対1に対応する。
以上の議論より、$${\mathrm{Spec}\ \mathbb{Z}[T] = \mathrm{Spec}\ \mathbb{Q}[T] \cup \bigcup_{p} \mathrm{Spec}\ \mathbb{F}_p[T]}$$とみなせる。
このことは後にファイバー積について述べるときにも確認する。

$${\mathrm{Spec}\ \mathbb{Z}[T]}$$も$${\mathrm{Spec}\ \mathbb{Z}}$$と同様に、個人的には以下の図をおすすめしたい。ただし、この図には注意があり、例えば$${(T^2 + 1)}$$に対応する直線は$${(2, T - 1)}$$（の近く）を通る。これについて詳しくは次節で述べる。

例1.1.8. $${\mathbb{C}[T_1, T_2]}$$の場合
簡潔に$${\mathrm{Spec}\ \mathbb{C}[T_1, T_2]}$$を述べることは難しいので、ここではいくつか例を述べることにする。
$${\mathbb{C}[T_1, T_2]}$$の素イデアルとしては$${(0), (T_2 - T_1^2), (T_1 - a_1, T_2 - a_2)\ (a_1, a_2 \in \mathbb{C})}$$などがある。
$${(T_1-a_1, T_2-a_2)}$$は$${\mathbb{C}^2}$$と1対1に対応している。
このことから、$${\mathrm{Spec}\ \mathbb{C}[T_1, T_2] \fallingdotseq \mathbb{C}^2}$$のように思えるが、$${\mathrm{Spec}\ \mathbb{C}[T_1, T_2]}$$には他にも$${(T_2-T_1^2)}$$などがあり、これは$${\mathbb{C}^2}$$の曲線$${T_2 = T_1^2}$$に対応する。
このように、幾何的な点のみではなく曲線（や曲面など）も点とみなすところが古典的な代数幾何との違いの1つでもある。