
①積分を初心者目線でわかりやすく解説
まいど!
理系大学院卒現役エンジニア
サイバーアカデミーのTAMOです。
今回は、
積分について
理解していただこうと思っています。
数学が苦手な方は
微分や積分でかなりの方が
挫折したかと思います。
特に積分に関しては
ラスボス感があったかと思います。
なにせこの謎の記号

が登場した時点で
人生詰んだ感ありませんでした?
安心してください、
この記号は大したことありません。
見た目が厳ついが中身は超キュートな
オジサンと同じ感覚でよいです。
そんなわけのわからない
記号や公式を覚えるよりも
中身を理解するのが大事です。
中身が理解できると
活用法がわかるので
仕事や日常に応用できます。
今回はこの中身を知っていただくための
内容となっていますので、
数式はほとんど出てきません。
実際に積分をゴリゴリ計算してく方法を
解説した記事は別に用意してありますので、
そちらをどうぞ。
式の立て方解説記事
式の計算方法の記事
では積分とは何か?
について初心者目線になって
できるだけわかりやすく解説していきます。
まず、こんな例を用意しました。
マイケルがアルバイトを始めました。
稼いだ金額は以下の通りでした。

ここで皆さんに質問です。
マイケルは、
4日目から7日目にかけて、
合計いくら稼ぎましたか?
4,000
+6,000
+7,000
+1,000
=18,000円
ですよね。
皆さん、おめでとうございます。
積分ができました。
以上。
は???
ってなりましたよね。
しかしこれが積分です。
積分とは、
ある区間の値を足し合わせて
その合計を求めること。
です。
簡単でしょ?
要は、
積分はただの足し算です。
じゃあ
なぜわざわざ高校にもなって改めて足し算を学ぶのか?
なぜあんな厳つい記号が登場したのか?
なぜ名前が足し算ではなく積分なのか?
説明していきます。
その理由は
小学生では解けない
足し算があるからです。
その例を紹介しましょう。
マイケルは
別のアルバイトを始めました
今回は時給制です。
ちょっと変わった時給制です。
初めの1時間は1,100円
そこから1時間経つごとに
時給が100円ずつ増えていきます。

つまり、
1時間目:1,100円
2時間目:1,200円
3時間目:1,300円
4時間目:1,400円
といった感じで増えていきます。
このルールで、
マイケルは4時間働いた場合、
マイケルは合計いくら稼ぎましたか?
1,100
+1,200
+1,300
+1,400
=5,000円
正解です。
先ほどとやり方は変わっていません。
ではここからが問題です。
従業員同士で不公平にならないために
時給の増え方を段階的ではなく
滑らかにしました。

厳密にルール決めされた
優良企業ですね。
さて、このルールで
マイケルは先ほどと同じ4時間働きました。
マイケルは合計いくら稼ぎましたか?
5,000円?
違います。
どう解くよ?
答えは5,200円です。
勘の鋭い方は
1,100円以下を四角形の部分を縦×横
1,100円~1,500円の三角形の部分を(縦×横)÷2
で解けたかと思います。

ではもっと意地悪に、
曲線を描いた上がり幅にしてみましょう。

いよいよそのような公式は使えません。
考え方は同じ足し算なのに、
時給の変化が滑らかになった瞬間、
小学生の足し算では
解けなくなってしまいました。
ここにはあるトリックがあります。
それは、
アナログとデジタルです。
別名、連続と離散です。
これについて詳しく解説している
記事を載せておきます。
【作成中】
要は、
小学生で扱っていた足し算は、
・指の本数
・階段の段数
・人の数
といったように
一つ一つ数えられる値であり、
これがデジタル(離散)な値です。
一方
・スロープの傾斜
・水の量
・車の速度
など、刻めば無限に存在する値
これがアナログ(連続)
と言います。
無限に刻むことができるというのは、
水の量でいうと、
1リットルと2リットルの間は?
1.5リットルや
1.35リットル
1.285654リットル
など無限に存在します。
一方指の本数に1.6本など存在しません。
音楽でいうと
・ピアノ:デジタル
・バイオリン:アナログ
高さでいうと
・階段:デジタル
・スロープ:アナログ
です。
ピアノはミとファの間はありませんが、
バイオリンなら実現できます。
30cm刻みの階段には
15cmの高さというものは存在しませんが、
スロープには存在します。

さてさて、
このアナログの足し算を可能にするために
積分という方法が存在します。
あの厳つい記号(インテグラル)は
これを可能にしてくれます。
先ほどの時給の問題を
馬鹿正直に足し算しようとすると、
1.1時間目の時給
1.12785時間目の時給
1.1278565485時間目の時給
など、
こんな感じで時間を無限に刻めますので、
馬鹿正直に足し算をやっていると
人生が終わってしまいます。
ちなみにこの時給問題を
積分を用いてとくと
こうなります。
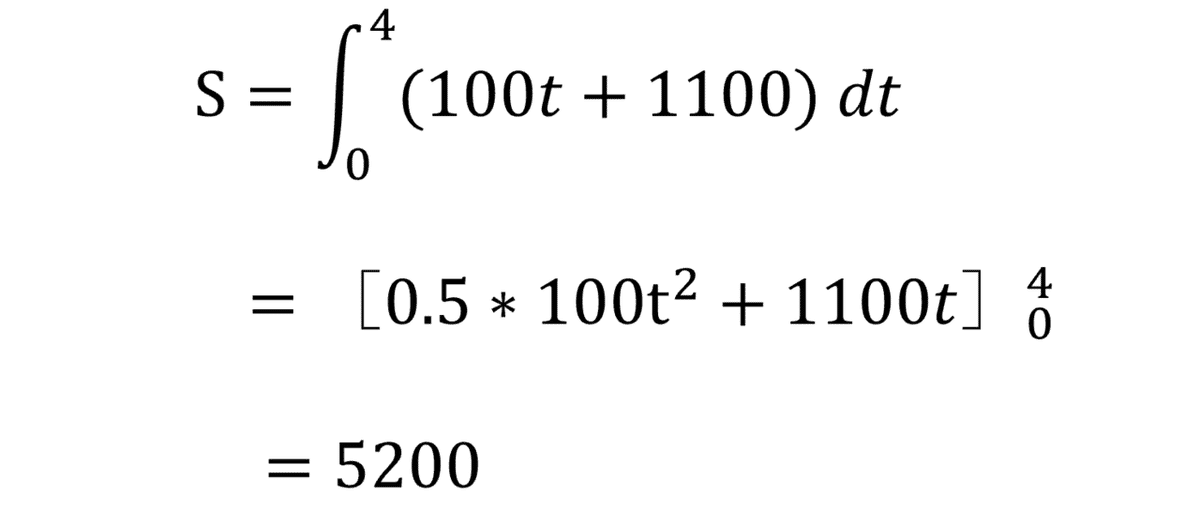
5,200円になりました。
この計算方法は今回の記事では
覚えなくてよいですよ!!
実際の計算方法はこちらの記事を見てください。
式の立て方解説記事
式の解き方解説記事
さて、
改めて積分とは何か一言で表すと、
積分とは
ある区間の
無限に刻まれた
値を足し合わせ、
その合計を
求める手段
です。
ということで積分が何なのか
だいたい理解いただけたかと思います。
以下の記事に、
実際の日常での応用例を紹介しています。
【作成中】
今回は以上です。
勉強すると頭疲れますよね。
ブドウ糖を消費している証拠です。
ブドウ糖が枯渇すると
頭の働きが悪くなるので、
ブドウ糖を適度に摂取しましょう。
以下におすすめのグッズを紹介しています。
ではまた。
