
良いアーリークロスの条件を数学的に考えてみた。
先日行われたJ2首位決戦。
SNS上で様々な議論を呼び起こしていましたが、キックという観点で見るとヴェルディの1点目をアシストした宮原選手のアーリークロスは完璧でした。
該当シーンはこちら。
アーリークロスの名手と言えば、アーノルドやデ・ブライネ、一昔前であればベッカムなどが思い浮かぶでしょうか。
💫 David Beckham 💫#RMHistory pic.twitter.com/uQYJogjzf2
— Real Madrid C.F. 🇬🇧🇺🇸 (@realmadriden) September 25, 2022
共通したボールの特徴としては、まず球速が速いこと、さらに相手の頭を超えて味方の頭にピンポイントで届くように落ちてくるようなイメージです。
よく言われる表現で言えば曲がって落ちるようなボールに近いと思います。
冒頭で掲載したヴェルディの宮原選手のクロスも例に漏れず球速が速く少し曲がりながら味方の頭にピッタリ落ちてくるボールです。
今回の記事では蹴り方自体ではなく、この質のボールがどのようにして実現しているのかを詳しく解説します。この記事を読むことで、このような弾道を実現するためには回転数やスピードに関してどのようなイメージを持って蹴れば良いのかを正しく理解できるようになります。
よくある誤解としては、曲がって落ちるボールを蹴るには横回転だけでなく縦回転成分を加える必要があり擦り上げるように蹴るべきというイメージが挙げられます。ここのイメージがズレているといくら練習してもうまく蹴れるようにはなりません。
実際上で挙げたシーンでも縦回転成分はほとんど加わっていないし、なんなら以下のようにバックスピンをかけたボールでも十分に相手の頭を超えて落ちるボールを蹴ることは可能です。
#OnThisDay in 2021, @rubendias scored his first goal for City! 💥 pic.twitter.com/WHmzr6290E
— Manchester City (@ManCity) February 27, 2023
この記事では数式がたくさん出てきますが、その後に出てくる図だけ見れば大体のことは分かるはずなので、物理・数学好きな変わり者以外はなんとなく読み飛ばしてうまく読んでもらえればと思います。
ボールの軌道を決める要素
まず、前提としてボールの軌道はどのようにして決定されるかを説明します。重要になる要素は大きく分けて3つで、
球速
回転
打ち出し角度
になります。
目的とする軌道に合わせて3つの要素を調節することが狙ったところへボールを蹴るための基本です。
今回の記事では、アーリークロスを目的とした場合のこの3つの要素の調整法を解説しますが、ロングキック、つまり飛距離を最大化することを目的にした場合の調整法については既に詳しく解説した記事があるのでこちらも是非。
空気抵抗がなければ放物線軌道
ここでは、単純化のために一旦空気抵抗(ボールが空気から受ける力)を無視してボールの軌道を考えます。
ボールが空気からの力を受けない場合、ボールの軌道は放物線になります。
そもそも放物線という名前自体が、放った物が描く線を指しているので当たり前ですね。
この記事のテーマはこの放物線軌道をどのように調整すれば目的とする場所に(味方のFWの頭に)、目的の軌道で(相手DFの頭を超えて落ちる)ボールを蹴ることができるかを考えることになります。
実際には空気抵抗によって軌道が変化
ここで無視することにしたボールが空気から受ける力は、実際にはボールの軌道を放物線軌道から外れて変化させる影響を持ちます。
これにはいくつか種類があって、一つは単純に抵抗というイメージの通り、進行方向と逆向きにかかるブレーキを掛けるような力です。これによってボールは減速されるので、簡単に言うと放物線軌道ほど遠くにボールは届きません。

もう一つは、進行方向に垂直な方向に受ける力で、横回転をかけるとボールが曲がるとか、バックスピンがかかると伸びるとか、無回転だとブレるとかの現象に関わる力です。
ここでは、その両方を無視して考えるので、先ほどの3つの要素で言うと回転の影響を無視して、速度・打ち出し角度を変えた時の軌道の変化を追った後、最後に改めて空気抵抗の影響を追加して考察を深める流れを取ります。
放物線軌道の調節
それでは、アーリークロスにおける放物線軌道の調節を具体的に考えていきましょう。
条件:到達位置一定。空気抵抗・回転は一旦無視。
アーリークロスの目的は、ある程度離れた距離にいる味方FWの頭にボールを届けることにあるので、第一の条件として放物線軌道が味方の頭がある特定の一点を通ることが挙げられます。
ある点から打ち出されてもう一点の特定の点を通る放物線軌道は無限に存在します。

上図の通り、初速v、地面からの打ち出し角度をθとして具体的に計算していきます。
まず、時間tにおけるx,y座標は以下の通りです。

ここからtを消去すると、初速をv、打ち出し角度をθとした時の放物線軌道の式が求められます。

今回の条件は、到達位置が味方FWの頭に来るようにすることなので、例えば40m先の高さ2.5mの位置にある味方FWの頭に合わせる場合を考えてみましょう。
ちなみに、クリロナのこの時の最高到達点が2.56mらしいのでクロスの受け手はほぼクリロナです。
✈️⚽️ @Cristiano#GoalOfTheDay pic.twitter.com/HIb5G5dLYN
— JuventusFC 🇬🇧🇺🇸 (@juventusfcen) December 18, 2021

そうすると、先ほどの式はこのような形になり、この等式を満たすv、θの組み合わせが、40m先のクリロナの頭にボールを合わせるための条件になります。
この式を満たすv、θの組み合わせをグラフとして図示すると以下の通りです。横軸がθ(°)、縦軸がv(km/h)となっています。

この図から打ち出し角度を45°近辺に設定すると、最も球速が遅いボールが届くことが分かります。とはいえ40m先に届けるためには時速70km以上の初速が必要であることが分かります。
これだけだと少し分かりにくいので、打ち出し角度が10°、20°、30°の時の軌道をそれぞれ図示してみます。
打ち出し角度だけ言われてもイメージしづらいと思うので、大体の目安を挙げておくとペナルティエリアのラインからゴールのクロスバーを直線で結ぶと約8.5°、PKのポイントからクロスバーだと約12.5°、ゴールエリアからクロスバーだと約24°くらいです。

上図の右上の四角には打ち出し角度とそのために必要な初速を記載していますが、赤線のように打ち出し角度10°の低くて速いボールで40m先に届けようとすると時速152kmの初速が必要です。
カタールW杯のスペイン戦で堂安が決めたゴールは見るからに球速が速く、実際W杯内の球速ランキングでは2位にランクインしたようですが、それでも時速120km程度だったようなのでこのスピードで蹴るのは厳しそうですね。
到達時間を短くするのは低くて速いボール
続いて、アーリークロスは到達時間が短い方が相手DFが反応できる時間が短くなって良いと考えられるので、到達時間について考えます。
先ほどの3つの打ち出し角度について時系列をそろえて到達位置を図示してみます。
まず打ち出し角度10°、初速152km/hのボールが到達した時点でそれぞれのボールがどこまで来ているかを図示すると以下の通りです。
打ち出し角度が30°になるとまだ半分にも到達していないことが分かります。

ただ、152km/hのボールを蹴るのは非現実的なので打ち出し角度が20°と30°の場合で比較してみましょう。
打ち出し角度20°のボールが到達した時点でのそれぞれのボールの位置を図示したのが下図です。
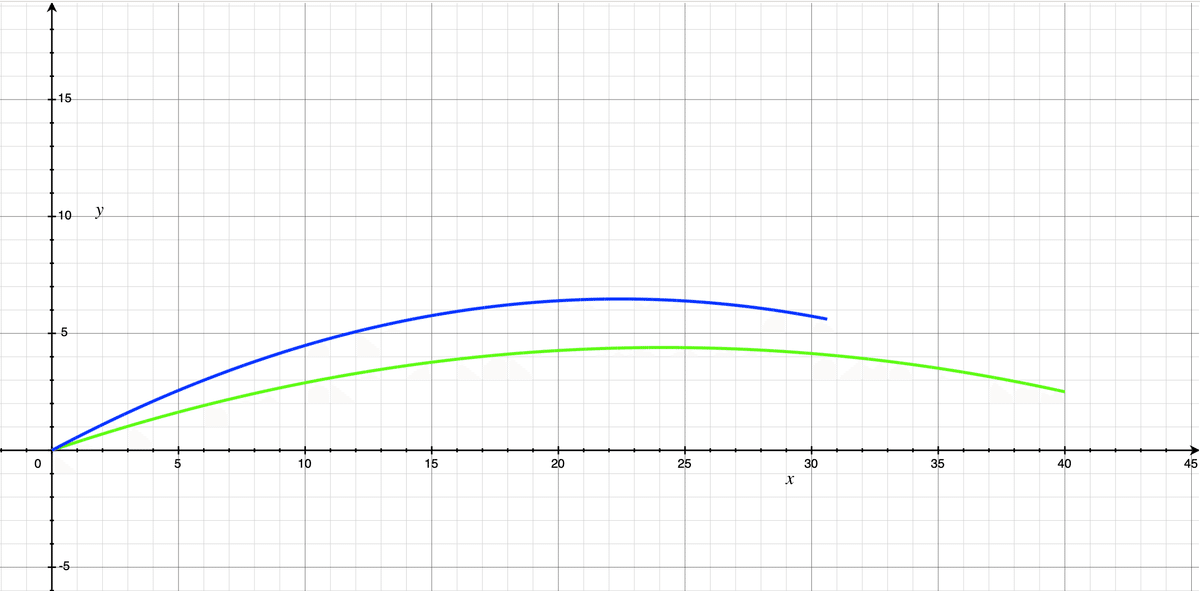
ここでもやはり10m以上の大きな差が付いており、打ち出し角度を小さく初速を速くすることが速く届けるためのポイントであると言えます。
具体的な数値で言うと、40m先の地点への到達時間は

より

で表されるので、

の式を用いてvを消去した上で縦軸を到達時間t、横軸を打ち出し角度θとして図示すると以下のようになります。

先ほど用いた3つの角度の例を見てみると、
打ち出し角度10°→0.96秒
打ち出し角度20°→1.57秒
打ち出し角度30°→2.05秒
となり、かなり大きな差が生じていることが分かります。
また、これだけであれば低くて速いボールの方が早く辿り着くという直感通りの結果でしかないのですが、数値的な計算をすることによってその変化の割合が直線に近いことも見えてきます。これがこの後、精度とスピードのバランスを考える上でポイントになります。
現実的には?
ここまで数値的な計算により大体のボールの軌道がどのようになるかは理解できたかと思いますが、ここからは実際に長い距離のクロスを蹴る際にどのようなイメージを持って、どのようなボールを目指すべきかを解説していきます。
※ここから先は有料エリアになります。
単品購入は以下のマガジン内から該当記事を選んでご購入ください。
また、月額制の定期購読マガジンであればよりお得に、しかもこれまでの記事(約20本)もすべて読めますのでぜひ以下のボタンからご購読ください!
ここから先は
Kicking lab
キックコーチ田所剛之によるトップ選手のキック分析記事をまとめて読めます。過去の記事も全部読めます。
この記事が気に入ったらチップで応援してみませんか?
