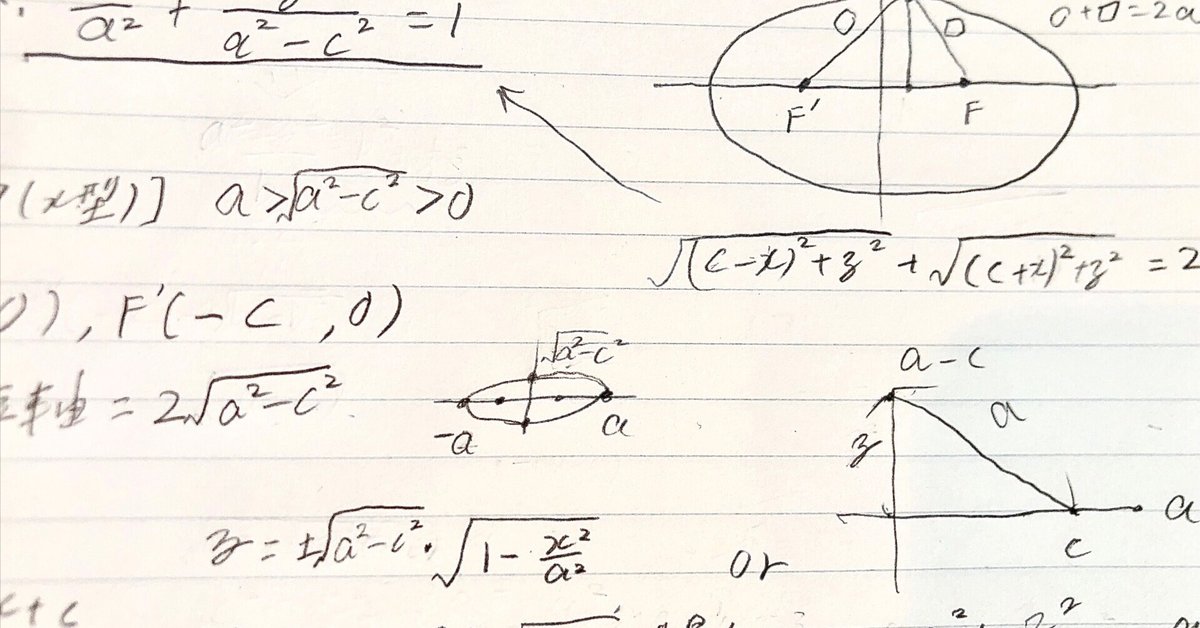
楕円の方程式に隠れた複素数を考える
どうも。まだ高校生です。本日、数学の学習をいつも通り進めていると、数学Cの範囲で習う、楕円の方程式と出会いました。最初はスムーズに理解できたのですが、楕円が縦長(正式名称ではないので使いたくはないが、分かりやすくするために使う。)の場合に計算がうまくいかず、恒等式になるはずの式が成り立たない事案が発生しました。
ほとんどの人は、教科書通りに勉強して、教えられた通りに公式を記憶しておれば、私みたいに悩むことはないかと思います。どうしても原理原則を理解したい私のような方に向けて、備忘録を書きたいと思います。
楕円の方程式とは
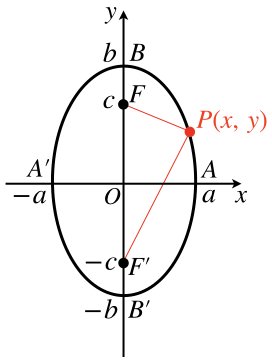
楕円の方程式とは、$${F(c,0)}$$、$${F'(-c,0)}$$からのキョリの和が$${2a}$$の時$${(a>c>0)}$$、$${\frac{x^2}{a^2}+\frac{y^2}{a^2-c^2}=1}$$というもの。これはピタゴラスの定理を使い、整理すれば簡単に導出できる公式です。
ただし、多くの教科書ではこの$${\frac{y^2}{a^2-c^2}}$$を、$${a^2-c^2=b^2}$$として置き換えて、$${\frac{y^2}{b^2}}$$としています。その方が円の方程式や、その他の計算で都合が良いからです。しかし私は原理原則に重きを置く人間です。$${\frac{y^2}{a^2-c^2}}$$と置いて計算したい。その方が個人的には計算だってしやすいからです。
これが今回の悩みの種になります。逆を言えば、多くの人はこの奥に秘められた謎を気にもせずに生きていることになるのです!(笑)

これが横長の楕円なら何も悩むことはありません。
楕円とx軸の交点のうち、プラスのものをAとした時、
焦点は$${F(c,0)}$$、$${F'(-c,0)}$$となり、長軸は$${2a}$$、短軸は$${2\sqrt{a^2-c^2}}$$であり、
証明すると、前者は$${FA+F'A=2a}$$(定義より)となり、$${2x=2a}$$、$${A=(a,0)}$$と簡単にわかります。また、後者においても、楕円とy軸との交点を$${B(0,y)}$$としたとき、ピタゴラスの定理より、$${c^2+y^2=a^2}$$から、$${y=\sqrt{a^2-c^2}}$$と簡単にわかります。
縦長では?
ではこれが縦長の時はどうでしょうか。
長軸が$${2\sqrt{a^2-c^2}}$$、短軸が$${2a}$$となってます。ではこれを証明したいですよね?少なくとも私は証明したくて仕方がありません。数学は対称性の下においてはとても美しいものですし、こんな線対称な図形なら長軸と短軸の長さが入れ替わったものだと言われても違和感はありません。しかし!それでも疑うのが私、また、なぜそうなるのかを知りたいのが私、まだ高校生です。
では先ほどと同じように証明してみましょう。先ほど簡単に証明ができた$${2a}$$、すなわち長軸を考えます。楕円とy軸の交点のうち、プラスのものを$${B(0,y)}$$とした時、$${FB+F'B=2a 、 (y-c)+(y+c)=2a}$$となるはずですが、教科書などには$${y=\sqrt{a^2-c^2}}$$とあります。では何が違うのか。実は、前提が違うのです。横長の楕円の場合、$${a>c>0}$$という仮定があります。これが違うのではないだろうかとわかりますね。
それでは次に短軸を証明しましょう。先ほどはピタゴラスの定理から簡単に証明できました。Bの値がどうやら$${y=\sqrt{a^2-c^2}}$$らしいと分かったので、それを前提に計算してみます。すると、$${a^2+c^2=\sqrt{a^2-c^2}^2}$$となります。ルートを外さなくても分かります。これは一致していません。では何がおかしいのでしょうか。実は、それぞれに仮定があるのです。横長の場合、$${a>\sqrt{a^2-c^2}>0}$$、縦長の場合、$${\sqrt{a^2-c^2}>a>0}$$となっています。当たり前だって?しかし!先ほども言ったように、教科書では$${a>b>0}$$のように書かれていて、何のことか分かりません。aとcの関係に気づくことが難しいのです。横長の計算はうまく行ったので、縦長の楕円に注目してみます。すると、$${a>0}$$は自明だから、$${\sqrt{a^2-c^2}>a>0 = a^2-c^2>a^2>0 = -c^2>0>0}$$となるのです。あれ?$${-c^2>0}$$って、$${c^2<0}$$となりますよね?これはそう、複素数になるんです!
複素数の意味
ではなぜ複素数になるのでしょうか。考えてみればわかりますが、a>c>0なら、必ず$${a>\sqrt{a^2-c^2}>0}$$になります。当たり前です。元のものから、元の元より小さいものを引いたものでは元のものの方が大きくなります。
図形的には、原点とAの間にFがあるということになります。
順番で言えば、
$${O,F,A}$$ です。
しかし縦長の時の仮定では$${c^2<0}$$が仮定です。どういうことか。
それは、焦点がどんどん小さくなると、その楕円は円になるからです。そして、原点に重なった焦点がそのまますれ違うように小さくなり続けると、また横長の楕円になってしまいます。
そうです。
$${O,A,F}$$ など存在しません。縦長の楕円は、焦点がy軸にないといけないのです。そこで、複素数平面のように、虚数がx軸に対して垂直方向に成長しているのです。
すると、縦長の楕円を計算するとき、今までcをxと同じように扱って計算しようとしていたことに気がつきます。だから、先ほどのように短軸=2aを三平方で証明しようとすると$${a^2+c^2=\sqrt{a^2-c^2}^2}$$のようにおかしな式になってしまったのです。
そこで、$${c^2=(ig)^2}$$(y軸上なので純虚数)に-1をかけて、本来処理されるはずだった$${i^2}$$を処理して、虚数から擬似的に実数に戻してやると上手くいきます。
まとめ
普通に図を見て考えればわかる話かもしれませんが、実際に証明しようとするとうまくいかないことというのはあります。
特に、世に出回っている$${\frac{y^2}{b^2}}$$という教えを鵜呑みにすると、しっかりとした理解ができません。
お役に立てたなら嬉しく思います。
ちなみに、$${x=\pm a\sqrt{1-\frac{y^2}{a^2-c^2}}}$$や、$${y=\pm \sqrt{a^2-c^2}\sqrt{1-\frac{x^2}{a^2}}}$$などの、楕円方程式を変形したものを考えれば、それぞれyが0の時、xが0の時を考えることによって、面倒な複素数などを考えなくても導出できるようになっています。
多くの教科書ではそう記述されているはずです。
また、複素数であるけどもそれに触れないように問題が構成されています。どういうことかというと、点Pから2つの焦点までのキョリの和と焦点の座標を駆使してやれば$${C^2}$$を無視して計算を進められるようになっているということです。"数学"じゃないよね。
それでは。
2024.6.25
