
【EV3で制御工学】PID制御によるMモータの速度制御④
前回の記事の続きです。
PD制御のプログラム
P制御とPI制御において、目標値に早く収束させるにはどうすればよいでしょうか。答えは簡単です。PゲインやIゲインを大きくすればよいのです。しかし、そうすると目標値付近で大きく振動するようになります。これを抑えるために、Dの項を追加します。まずは、Pの項とDの項だけを考えたPD制御のプログラムを作っていきます。
P制御のプログラムにDの項を追加していきます。追加で必要な変数を用意しておきましょう。
last_e … 前回の偏差($${e[k-1]}$$に相当するもの)(初期値:0としておく)
Kd … Dゲイン(初期値:適当な値に設定しましょう)
P制御のときと同じくファイルの削除を行います。右上にファイル名「PD」を入力しておき、「削除」モードにします。また、タイマーをリセットしておきます。

これで下準備は完了です。制御部分を作っていきましょう。
続いて、偏差の計算部分、Pの項の計算部分を作ります。P制御とPI制御のときと全く同じなのでここでは省略します。
続いて、Dの項($${D=K_d(e[k]-e[k-1])}$$)を書いていきます。$${e[k-1]}$$は変数「last_e」に入っています。計算結果をいったんDという変数に入れておきます。
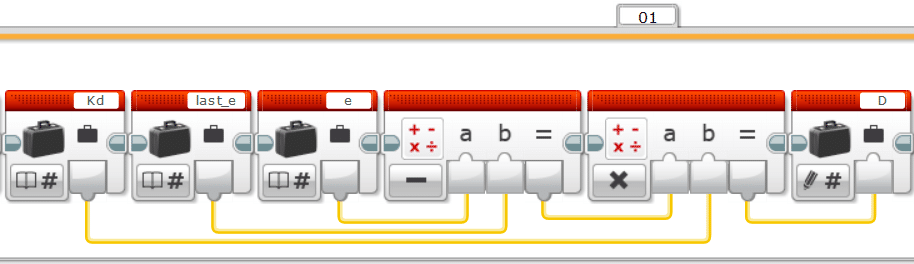
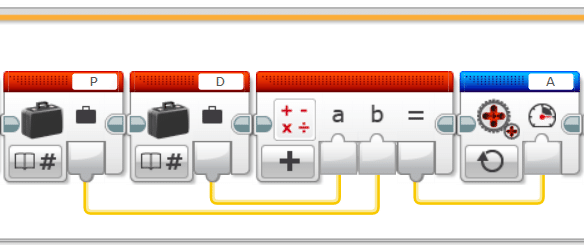
PD制御はPの項とDの項の和を計算結果として入力します。モータを動かすのには、青色の「未調整のモータブロック」を用います。
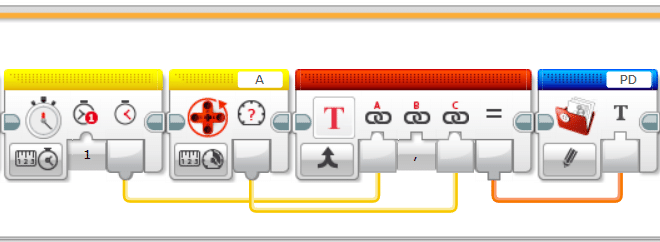
次に、時系列データをファイルの保存していきます。P制御、PI制御のときと同じなので詳細な説明は省略します。
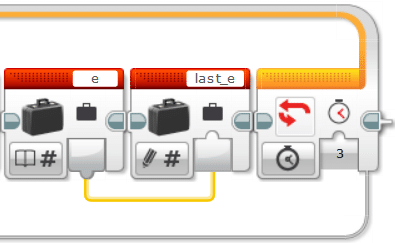
そして最後に大切なのが、last_eの更新です。毎回、last_eにeを代入しておく必要があります。ループの終了条件は「時間」としておきましょう(時間は適当に設定しましょう)。
出来たら動かしてみましょう。
グラフ(簡易版)の作成
インテリジェントの同じプロジェクト内に「PD.rtf」というファイルができていると思います。このファイルをPCにアップロードしましょう。
アップロード出来たら「PD.rtf」を前回の記事で示した手順で「.xlsx」(Excelファイル)に変換します。あとはExcelで散布図のグラフを描くとモータの動作の様子をグラフで確認できるようになります。
最終的にはPythonを用いて次のようなきれいなグラフを作ります。
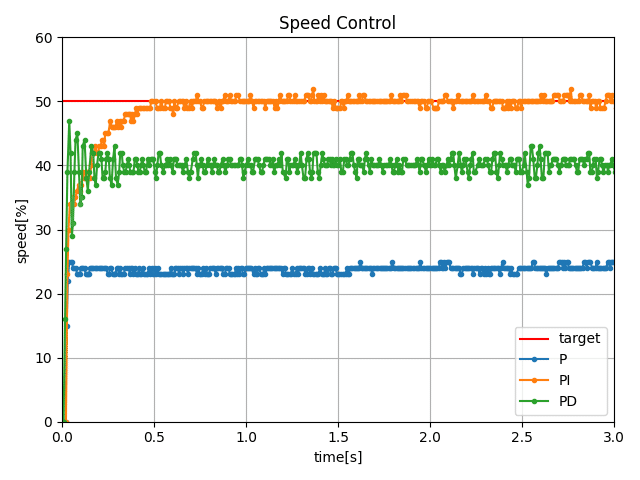
このグラフでは、PD制御のPゲインを5としています。P制御でPゲインを5にしたときは、それに比べてもっと振動してしまいます。Dの項を入れることで振動が抑えられるので、Pゲインを大きくしては約収束に向かわせることができました。しかし、やはりIの項がないと目標値に収束しません。
まとめ
今回ははここまで。P制御の代わりにPD制御を導入することでPゲインを大きくして早く収束に向かわせることができることを確認しました。次回は、Pの項、Iの項、Dの項のすべてを導入して、PID制御のプログラムを作ります。⑤に続きます。
