
【EV3で制御工学】PID制御によるMモータの速度制御②
前回の記事の続きです。
離散化
実際にロボットなどを制御するときは、連続時間ではなく離散時間(飛び飛びの時間)を考える必要があります。今回のMモータの速度制御においても、モータの回転数の測定が何ミリ秒という間隔でしか行えないので、離散時間で考えていきます。
PID制御の式の離散化
前回の記事で、PID制御の入力は以下の式で表せると説明しました。今回は、時間間隔を$${\Delta t}$$とし、$${k}$$ステップ目の入力、偏差をそれぞれ$${u[k]}$$、$${e[k]}$$と表すこととします。PID制御の入力の離散化した式は次のように表せます。
$${u[k]=K_pe[k]+K_i\sum\limits_{l=0}^{k}e[l]\Delta t+K_d\frac{e[k]-e[k-1]}{\Delta t}}$$
比例については何も変わっていないようなものですね。微積分については、それぞれもともとの定義を考えればわかると思います。当たり前ですが、$${\Delta t \rightarrow 0}$$と極限を取れば、離散化前の元の式に戻ります。
今回は、時間間隔$${\Delta t}$$が一定であると考えます。そうすると、入力の式は次のように表せます。
$${u[k]=K_pe[k]+K_i\sum\limits_{l=0}^{k}e[l]+K_d(e[k]-e[k-1])}$$
ただし、$${K_i}$$と$${K_d}$$は先ほどの式と同じ値ではないことに注意が必要です。
プログラムを作る準備
では、PID制御によるMモータの速度制御のプログラムを作っていきましょう。EV3ソフトウェアを使います。MモータをインテリジェントブロックのポートAに接続しておきましょう。
P制御のプログラム
まずはP制御のプログラムを作っていきます。必要な変数を用意しておきましょう。
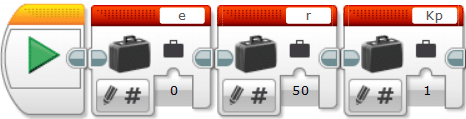
e … 偏差(初期値:0としておく)
r … 目標値(初期値:適当な値に設定しましょう)
Kp … Pゲイン(初期値:適当な値に設定しましょう)
今回は、時系列データを保存しておいて最終的にグラフ化をしてPID制御の性能を確認します。そこで、普段あまり使わない青色の「ファイルアクセス」ブロックを使っていきます。

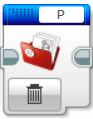
まずは、ファイルの削除を行います。右上にファイル名「P」を入力しておき、「削除」モードにします。これでインテリジェントブロックの同じ名前のプロジェクト内の同じ名前のファイルを削除することができます(削除しておかないと、データが上書きではなく追加で書き込まれてしまいます)。
次に、タイマーをリセットします。

これで下準備は完了です。制御部分を作っていきましょう。
まずはループを用意しましょう。次に、偏差の計算式$${e[k]=r[k]-y[k]}$$を書きます。ただし、測定値$${r[k]}$$は黄色の「モータ回転」ブロックの「現在のパワー」モードを用いて測定します。前回も言及しましたが、これは正確には「パワー」ではなく「スピード」を測定しています。
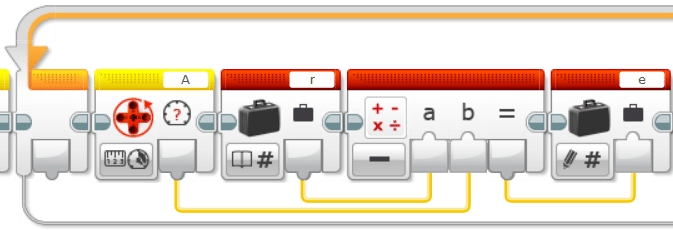
次に、入力を計算していきます。まずはP制御なので、Pの項($${P=K_pe[k]}$$)だけを書いていきます。計算結果をいったんPという変数に入れておきます(IやDが出てくるとデータワイヤが重なりまくって見にくくなるのであらかじめ)。
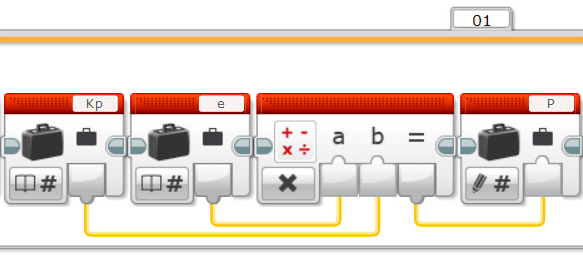
計算結果を入力していきます。モータを動かすのには、緑色のブロックではなく青色の「未調整のモータブロック」を用います。
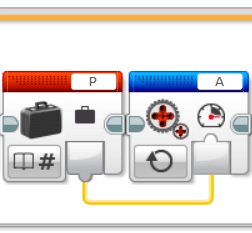
最後に、時系列データをファイルの保存していきます。「ファイルアクセス」ブロックの「書き込み」モードを使います。「タイマー」ブロックで取得した時刻と「モータ回転」ブロックの測定データを、赤色の「テキスト」ブロックを用いて「,」でつなぎ、「P」というファイルに書き込みます。ちなみに、このファイルは「.rtf」(リッチテキストファイル)という形式です。また、この「ファイルアクセス」ブロックの「書き込み」モードは書き込むたびに勝手に改行してくれます。ループの終了条件は「時間」としておきましょう(時間は適当に設定しましょう)。
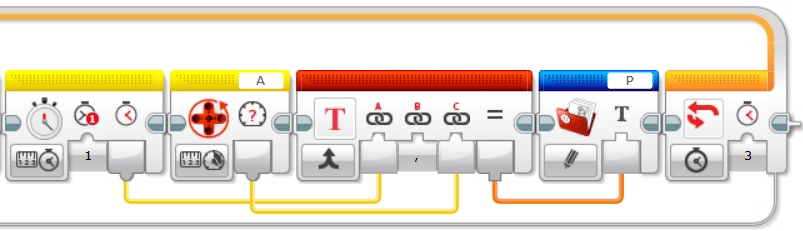
出来たら動かしてみましょう。
グラフ(簡易版)の作成
インテリジェントの同じプロジェクト内に「P.rtf」というファイルができていると思います。このファイルを次のページを参考にしてPCにアップロードしましょう。
アップロード出来たら「P.rtf」をWordなどを用いて「.txt」テキストファイルに変換しましょう。次に、拡張子を無理やり「.csv」と書き換えてCSVファイルにします。そのファイルをExcelで開き、「.xlsx」(Excelファイル)として保存します。あとはExcelで散布図のグラフを描くとモータの動作の様子をグラフで確認できるようになります。
最終的にはPythonを用いて次のようなきれいなグラフを作ります。
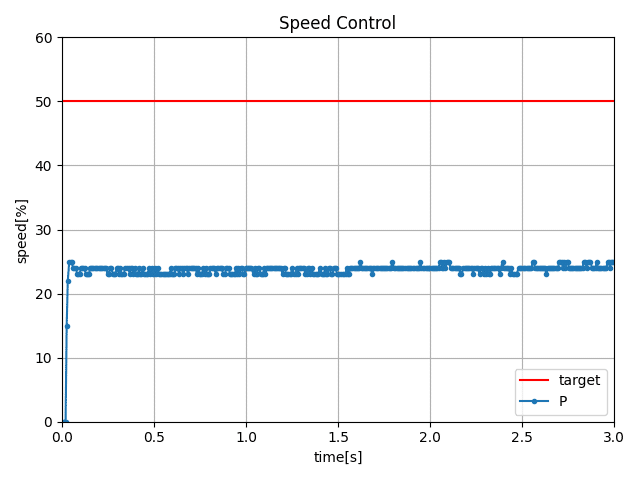
あれあれ?目標値とは程遠いところで収束してしまっています。おかしいと思うかもしれませんが、実はこれで正解です。Pゲインを大きくすると少しマシになりますが、振動するうえに、それでもなお定常偏差(目標値との差)が残ります。
前回少し言及しましたが、EV3のMモータはざっくりいうとDCモータで、回転速度は印加電圧にほぼ比例します。DCモータはLR回路とほぼ等価なので1次遅れ系とみなせます。めちゃくちゃ簡単に言うと、入力してちょっとだけ遅れてからその効果が表れます。そのため、定常偏差が残るのです。この定常偏差をなくすためにIの項を追加します(n次遅れ系は積分器がn個あると定常偏差がなくなります)。
まとめ
今回ははここまで。離散時間でのPID制御について考えました。また、P制御によるMモータの速度制御のプログラムを作成し、実行結果について解説しました。③に続きます。
