見出し画像

【EV3で制御工学】PID制御によるMモータの速度制御①

Taiyo

今回は解説記事です。LEGO Mindstorms EV3を題材にして制御工学っぽいお話を書いてみようと思います。PID制御でMモータの速度制御をしてみました。EV3を触ったことのある人（どちらかと言えば上級者）向けですが、制御工学初心者にも伝わるように書いてみました。


用いたもの

PID制御の実現のために用いたもの

  • LEGO Mindstorms EV3

  • EV3ソフトウェア

グラフの描画のために用いたもの

  • VSCode（Pythonの実行可能環境であればなんでもよい）

  • Pythonのライブラリ：pandas、matplotlib

フィードバック制御

制御の目的は、制御対象の出力（応答）を目標値と一致させることです（ここでは、出力のことを測定値と呼ぶことにします）。今回のMモータの速度制御で言えば、Mモータを目標のスピードで回転させることです。普通にパワー（電圧）を決めてやればええやんと思うかもしれませんが、モータを用いてロボットを走らせる場合などには負荷が生じ、単にパワー（電圧）を指定するだけでは所望のスピードで回ってくれないことがあります。そこで今回は、測定値を目標値と比較して適切な入力を決定するフィードバック制御の1つであるPID制御を導入します。

フィードバック制御

EV3 Mモータの特性

まずは、EV3のMモータの仕様について簡単に解説していきたいと思います。EV3のMモータは、角度や回転速度を調べることのできるサーボモータです。EV3ソフトウェアではみなさんおなじみ緑色のブロックで動かせます。

みなさんおなじみ緑色のブロック

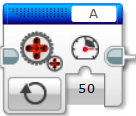
「50」と書いてあるのが「パワー」となっていますが、実はこれは「スピード」です。実はこの緑色のブロックは、スピードが「50」になるようにフィードバック制御をしているのです。今回はこれは使いません。というか、これ（に近いもの）を作ります。使うのは、青色の「未調整のモータ」ブロックです。

今回使う「未調整のモータ」ブロック

このブロックを使うと、MモータをただのDCモータのように扱えます。一切フィードバックを行わない形で入力を与えます。この「50」こそ「パワー」なのです。EV3ソフトウェアでプログラムを書いているときは意識することはありませんが、実際にはPWM制御（高速でON/OFFを切り替える制御法）によって電圧を入力することで動かしています。「50」はデューティ比[%]（ONの割合）です。DCモータは定常状態（ずっと動いてるとき）のとき、回転速度が入力電圧に（ほぼ）比例するという特性を持っています。わざわざ「定常状態」と書いたのは、今回主に観察するのが「過渡状態」（動き始めのとき）だからです。過渡状態を考えるとき、DCモータは（コイルと抵抗からなるLR回路とほぼ等価なので）1次遅れ系とみなすことができます（後で伏線回収します）。

「スピード」の測定には次の黄色の「モータ回転」の測定ブロックの「現在のパワー」モードを用います。これまた「パワー」とありますが、測定しているのは「スピード」です。

「モータ回転」の測定ブロック（「現在のパワー」モード）

PID制御とは

PID制御はフィードバック制御の一種です。P、I、Dはそれぞれ、Proportional（比例）、Integral（積分）、Derivative（微分）の頭文字で、これらの要素を組み合わせて制御を行います。Pは、目標と現在の状態の差に比例して制御を行います。Iは、過去の差の累積をなくすように制御します。また、Dは変化の速さを考慮して振動を抑えます。

以降、時刻$${t}$$での目標値を$${r(t)}$$、入力を$${u(t)}$$、応答を$${y(t)}$$とします。また、応答と目標値の「偏差」を$${e(t)=r(t)-y(t)}$$と表します。PID制御では、次の式のように入力がPの項、Iの項、Dの項の和で表されます。以下では、各項についてそれぞれ詳しく解説していきます。

$${u(t)=K_pe(t)+K_i\int_{0}^{t}e(\tau)d\tau+K_d\frac{de(t)}{dt}}$$

Pの項

ここでは、$${K_pe(t)}$$をPの項と呼ぶことにします。これは皆さんご存知、ただの比例の式ですね。比例と言えば$${y=ax}$$という式がイメージとして湧くと思いますが、それと全く同じ構造です。言葉で説明すると、偏差=目標値からのズレ具合に比例して入力を決定するということです。$${K_p}$$は比例係数にあたるもので、「Pゲイン」や「比例ゲイン」と呼びます。

Iの項

ここでは、$${K_i\int_{0}^{t}e(\tau)d\tau}$$をIの項と呼ぶことにします。$${\int}$$はみんな大好き積分記号ですね。積分というのはざっくり言うと「足し算」です。$${\int_{0}^{t}e(\tau)d\tau}$$という式は、時刻0からtまでの偏差$${e(t)}$$の積分、すなわち累積を表しています。つまり、これまでの「ズレ」の合計を入力に追加するということです。$${K_i}$$は比例係数にあたるもので、「Iゲイン」や「積分ゲイン」と呼びます。

Dの項

ここでは、$${K_d\frac{de(t)}{dt}}$$をDの項と呼ぶことにします。みんな大好き微分ですね。微分というのはざっくり言うと「変化の大きさ」です。$${\frac{de(t)}{dt}}$$という式は、時刻tで偏差を時間で微分したものです。つまり、「ズレ」の変化の度合いによって入力を変化させるということです。$${K_d}$$は比例係数にあたるもので、「Dゲイン」や「微分ゲイン」と呼びます。

まとめ

今回ははここまで。やろうとしていることとPID制御の基本的な考え方について解説しました。②に続きます。

この記事が気に入ったらサポートをしてみませんか？