
【EV3で制御工学】PID制御によるMモータの速度制御⑤
前回の記事の続きです。
PID制御のプログラム
いよいよ、PID制御のプログラムを作っていきます。PID制御を用いると、定常偏差なく、早く目標値付近に収束させることができます。
では、いつも通りの手順でプログラムを作っていきましょう。
まず、各変数の設定と初期化を行います。また、ファイルの削除を行います。右上にファイル名「PID」を入力しておき、「削除」モードにします。タイマーもリセットしておきます。

これで下準備は完了です。制御部分を作っていきましょう。
まず、偏差の計算部分を作ります。$${e[k]=r[k]-y[k]}$$ですね。
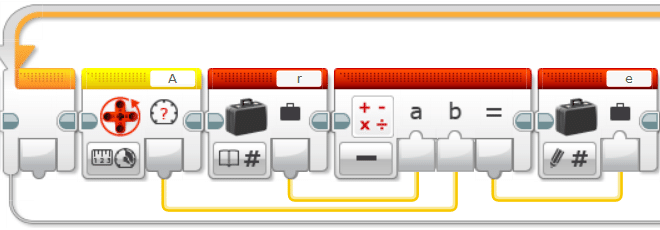
次に、Pの項の計算部分を作ります。$${P=K_pe[k]}$$ですね。計算結果をいったんPという変数に入れておきます。
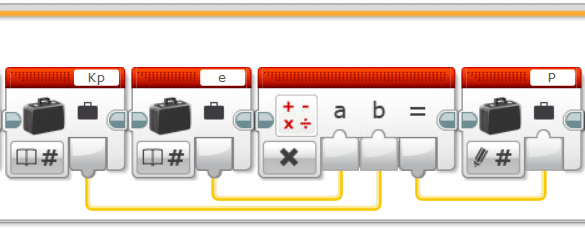
続いて、sum_eを更新して、Iの項を書いていきます。$${I=K_i\sum\limits_{l=0}^{k}e[l]}$$ですね。$${\sum\limits_{l=0}^{k}e[l]}$$は変数「sum_e」に入っています。計算結果をいったんIという変数に入れておきます。

さらに、Dの項を書いていきます。$${D=K_d(e[k]-e[k-1])}$$ですね。$${e[k-1]}$$は変数「last_e」に入っています。計算結果をいったんDという変数に入れておきます。
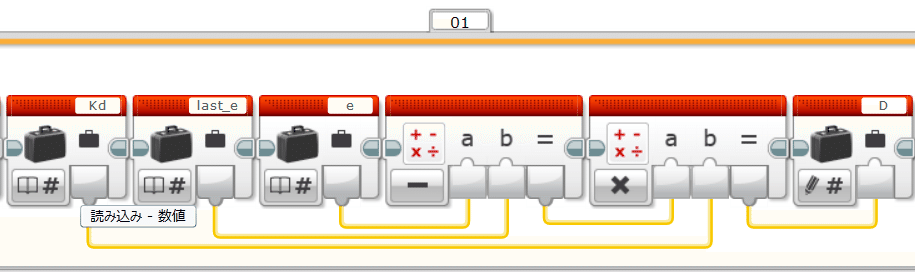
PID制御はPの項とIの項、Dの項の和を計算結果として入力します。モータを動かすのには、青色の「未調整のモータブロック」を用います。

次に、時系列データをファイルの保存していきます。これまでと同じなので詳細な説明は省略します。そして最後にlast_eの更新を忘れないようにしましょう。ループの終了条件は「時間」としておきましょう(時間は適当に設定しましょう)。

出来たら動かしてみましょう。
グラフ(簡易版)の作成
インテリジェントの同じプロジェクト内に「PID.rtf」というファイルができていると思います。このファイルをPCにアップロードしましょう。
アップロード出来たら「PID.rtf」を前回までの記事で示した手順で「.xlsx」(Excelファイル)に変換します。あとはExcelで散布図のグラフを描くとモータの動作の様子をグラフで確認できるようになります。
最終的にはPythonを用いて次のようなきれいなグラフを作ります。

このグラフでは、これまでのP、PI、PD制御とPID制御の実行結果を比較しています。PID制御については、(実験的に)各ゲインを適切な値に設定しています。PID制御を導入することで、定常偏差なく、早く目標値に収束させることができるていることがわかります。
まとめ
今回はここまで。PID制御を導入することで、定常偏差なく、早く目標値に収束させることができることを確認しました。次回はおまけです。Pythonできれいなグラフを作りましょう。⑥に続きます。
