実験実習 課題2の解説:リチャード・セイラー ナッジ 時間割引
の課題2の解説である。

参考1:神経経済学Neuroeconomicsにおける時間選好time preferenceや異時点間選択intertemporal choiceに興味がある場合はこのリンクを参照のこと。PDFはここ
参考2:心理物理学的に双曲割引を導出した研究論文はこちら (PDFはここ)日本語解説はこちら
----------------------------------------------------------------------------
実社会における初等的解説が、日本生命のコラムにおいてなされているので、こちらも参照のこと。
執筆者:
岩﨑 敬子氏(2020年12月12日(土)~13日(日)開催の行動経済学会大会において引用内容などをご本人にチェックしていただきました)
株式会社ニッセイ基礎研究所、保険研究部 研究員
研究・専門分野:災害復興、金融・健康行動、メンタルヘルス、ソーシャル・キャピタル
-----------------------------------------------------------------------------------
また、2020年の上記学会でナッジ(nudge)に関係するご発表をされていたNTTサービスエボリューション研究所 佐藤妙様からは、ナッジの社会実装のための技術開発の紹介として、下記の記事を講義用参考資料としてご提供いただきました(2020年12月23日):
■NTT技術ジャーナル
” 人と環境の関係をとらえ、自然な働きかけで人の行動を支援するアンビエントアシスト技術”
https://www.ntt.co.jp/journal/1912/JN20191219_h.html
--------------------------------------------------------------------------------------
Paul Samuelson(1937)によって提唱された割引効用モデルにおいては、時点tで消費する財xの効用は
U(x, t)=u(x)D(t)
と、時間によらない効用関数u(x)と時間割引関数D(t)との積の形に分離できると仮定されていた。
ここで時間割引率DR(discount rate)を以下のように定義する:

時間割引率(上の式からわかるように、単位は1/時間)は一般には時間の関数であるが、「時間整合性」(time-consistencty)を意思決定者がもつ場合には、時間tによらない定数となる。
この場合には、時間割引関数は
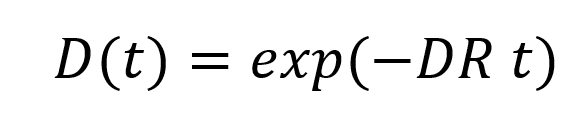
と指数関数の形に表現できることが知られている(時間割引率の定義式を-dD/D=定数dtと式変形してから両辺を積分公式∫(1/x)dx=ln(x)+Cと∫定数dx=x+Cを用いて積分し、両辺をexpの肩にのっければわかる→実際にやってみたのはこちら)。ここでDRは時間によらないという意味の定数(指数関数割引における時間割引率)である。
ただし、exp(x)は指数関数(exponential function)であり、以下のように定義される(Taylor展開による定義):
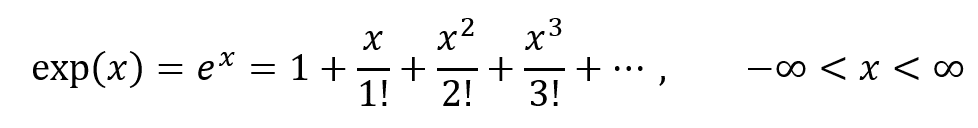
(このテイラー展開の第一項は1という無次元量なので、この項と足し算することが許される第二項以降はすべて無次元量でなくてはならない。ここからロジカルに考えると、そもそもexp(x)の引数xが単位のない量でないと、物理学的に間違っている式になってしまうことになる。したがってtの前に掛け算されているDRは1/時間という次元をもつことがここでも確認できる)
今回の実験課題で、成立する
U(1500, 0)=U(a, 3/12 年), U(1500, 0)=U(b, 1年), U(1500, 0)=U(c, 3年)
という関係式3本に対して
①時間整合性(すなわち指数関数割引)、
記号的には[DR(t)=DR(t') for all t, t']
②お金(による消費)の時間によらない価値がu(x)=x と線形な効用関数であらわされる(この仮定は、ミクロ経済学的には、もらえるお金が金額的に少なく、富を一定とみなせるという仮定のもと、受け取ったお金を一種類の財に集中して消費にあてたり、貯蓄してしまったりするのではなく、受領時点でいろんなものやサービスにばらして消費してしまう、という仮定である。詳しくは、社会全体の「良さ」=社会厚生を分析する部分均衡分析における余剰分析について学ぶと理解できるであろう。お金をこのようにとらえると、報酬ではなく、価値尺度財=ニュメレールとみなすことができる。ラグランジュ未定乗数法の概念でいえば、予算制約式の乗数が、所得のシャドープライスに対応している。金額が大きい場合でも所得の限界効用が一定であるためには、消費者の効用関数がホモセティック型----各財の消費量たちの同次関数の単調変換関数----である必要がある。)
記号的には[u(x)=x for all x]
という2つの独立な仮定を同時にすると3か月後、1年後、3年後の意思決定に関する年利を用いて、
1500 exp( - DR_3m ×0)=a exp(-DR_3m ×(3/12) y) においてexp(0)=1 を用いると左辺=1500となる、などより

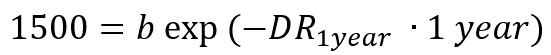
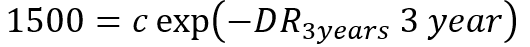
というデータに基づいた3本の関係式 ・・・・・・・・・・③
が得られる。
ただし、DR_3months は3か月に消費できる報酬の時間割引率、などである。
ここで、そもそも上記の3本の式をたてるときに時間整合性(時間割引率DRがどの時点でも同じ)を仮定していたので、もしこの仮定が正しければ、
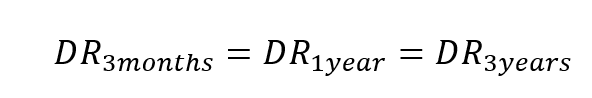
という式が成立するはずである。このことを人間を対象に検証し、それまでの新古典派経済学で仮定されていた時間整合性が成立しないことを示したのが、行動経済学者リチャード・セイラー(ノーベル経済学賞受賞)である。
データ解析のために、
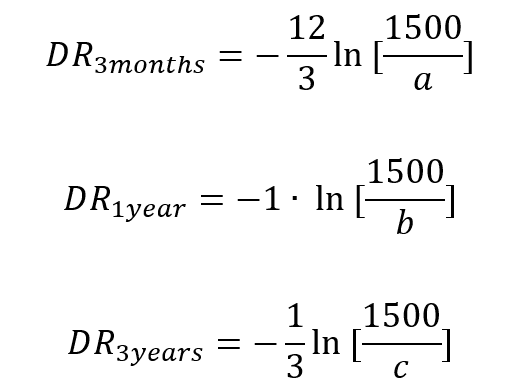
という表式を得ておいて、データa,b,cを代入すると、多くの人では
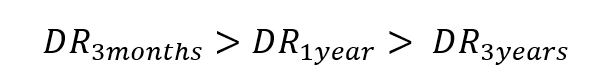
という、DRが各時点においてことなるという時間非整合性がみられる。また、この不等式のように遠い将来のほうが近い将来よりもDRが小さい異時点間選択行動のことを、双曲割引(hyperbolic discounting)とよぶ。このように各時点における時間選好が同一個人内で異なってしまう場合には、どのDRがその人の真の選好であるか不明なため、合理的なインセンティブに基づいた社会政策(個人の選好が1通りに定義されているときのみ可能)のかわりに、非インセンティブ的な方法が必要となる可能性がある。このような方法を、リチャード・セイラーはナッジ(nudge)とよんだ。以下に、Thaler1981のオリジナルデータ(1ドル=100円とした場合、a=3000円, b=6000円, c=10000円 )の解析ファイル(エクセル)を置いておくので、自分のデータ解析に利用してもよい。(Thaler 1981 Economics Lettersより一部抜粋) (ただし、金額が1500円の場合のみを解析しているので、U(1500, t)をV(t)という略称で表記している。

市場におけるDR(t)
資産市場では、平常時には、リスクフリー資産(債券bond)に関して、満期まで(購入した債券を現金として受領できるまで)の期間が長いほうが金利(interest rate)が大きい(DR_3m < DR_1y < DR_3y)。このことを順イールドyieldと呼ぶ(我々の脳や心の働きによる通常の時間選好のパターン(双曲割引)とは逆である)。また、各時点のDR(t)をつないだ曲線をイールドカーブyield curveと呼ぶ。一方、金融引き締め時や不況(recession)の前には、逆イールドとなり、双曲割引のような傾向となる。フラットなイールドカーブはDR'(t)=0 for all tのことなので、指数関数割引に対応する。このような時間割引率time-discount rate(リスクフリー資産なので時間選好率time preferenceに一致すると考えられる)が現金化できるまでの期間の長さによって異なることを、金利の期間構造(term structure)とよぶ。実務用の解説は大和証券の金融・証券用語解説 [イールドカーブ]の下記リンク(https://www.daiwa.jp/glossary/YST0048.html 2020年12月27日訪問)を参照。このような金利の期間構造が存在することや、イールドカーブ(時間選好の時間による変化の曲線、時間割引曲線D(t)ではなく、DR(t)のことである)の形状が順(DR'(t)>0 右上がり 逆双曲割引的)から逆(DR'(t)<0 右下がり 双曲割引的)に変化することの理由は、十分には解明されていない。
効率市場仮説(EMH, Efficient Market Hypothesis)とよばれる、債券を含めた価格が、すべての情報を織り込んで形成されているという仮定をおいて、債券価格や金利が、想定外の出来事のみに反応して変動するため、ランダムな確率過程としてモデル化できる、として金利の期間構造と債券価格との関係を確率微分方程式によってモデル化している研究の解説は、"Impact of Different Interest Rate Models on Bond Value Measures." Buetow et al.である。もし、無裁定条件(no arbitrage)という、目前の資産価格にすべての情報が合理的に織り込まれていて、だれもそれよりも真な価格で売買できない、という市場の効率性を仮定した場合は、一般に以下の確率微分方程式1であらわされる(Buetow et al.からの引用)。また、(1)のzは、植物学者ブラウンが発見した、花粉から出てくる微粒子が水面上でランダムに運動する(ただしこの動きは、生命性とは関係なく、熱運動によるものであった)様子のモデルである「ブラウン運動」を、アインシュタインが熱統計力学をもちいて分子論的に理論解析する際にもちいたランダム・ウオークの確率過程で、ウィーナー過程とよばれるものである。

http://janroman.dhis.org/finance/Interest%20Rates/3%20interest%20rates%20models.pdf
2019年8月には、米国債のイールドカーブの逆転がおこり、Wall Street Journalなどでも、世界に迫りつつあるなんらかのグローバルなマクロ変動による災難を告げる不吉な予兆として警戒心をもって取り扱われた( https://www.wsj.com/articles/yield-curve-telegraphs-recession-but-its-wires-are-crossed-11565697600 2020年12月27日 訪問)。5年以内のDR(t)が、双曲割引のように右下がりのイールドカーブになっていることがわかる。

また、欧州の中央銀行のサイト( https://www.ecb.europa.eu/stats/financial_markets_and_interest_rates/euro_area_yield_curves/html/index.en.html 2020年12月27日訪問)では、イールドカーブの形状が掲載されている。このグラフを見ると、逆双曲割引的であることが一見してわかるであろう。また、2020年12月においては、どの時点でもDR(t)<0である(マイナス金利とよぶ)。このような負の時間選好(negative time preference)は、行動経済学では、以下の論文で扱われている:
Negative Time Preference
George Loewenstein and Drazen Prelec American Economic Review, 1991, vol. 81, issue 2, 347-52

また、我が国においては、2008年の金融危機において失業率が上昇したことから、中央銀行(日銀)によって、金融緩和が開始され、2016年以来、このイールドカーブの形状パラメータを調節すること(YCC)が試みられているが、2020年現在は、失業率や物価などへの社会経済的効果は未知数である(ブルームバーグAlister Bull 2020年6月23日 9:46 JST):
「日銀のYCCは「まだ結論出ていない」、物価目標達成巡り-NY連銀」
マイナス金利政策とは、市場の時間選好DR(t)<0とする政策であり、YCC(イールドカーブコントロール)政策とは、市場のDR’(t)(時間選好DR(t)の時間による微係数)をコントロールする政策である。このように、実社会の失業率を低下させるためにも、DR(t)とDR'(t)との2種類の変数を質的に区別することが重要であることがわかるだろう。
(日銀によるYCC:DR'(t)の操作の公開資料は日銀のHPのリンクを参照
『金融政策:2%の「物価安定の目標」と「長短金利操作付き量的・質的金融緩和」』(2020年12月21日訪問)
企業価値評価における時間割引

企業価値の計算に必要な数字は、たとえばullet http://www.ullet.com/ などの数字から推定することも可能なので、将来就職する予定の会社について算定してみると、就職先の選定に役立つだろう。
データ解析のロジック
以上のデータ分析で用いた科学的推論よる結論の導き方は、論理学的には、仮説演繹法とよばれる帰納法の一種である。今の場合はこの仮説演繹法に背理法(命題pを仮定してq∧ not qという矛盾を導くことによってnot pであることを結論する方法)を組み合わせることによって、時間整合性というtに関する全称命題が成立していないことが結論された。具体的に今のThalerが行ったロジック操作の例では、
P: ①∧② Q:③ R:not① S:Q→R T:P→Q
としたときに、SとTが真であるため、Pを仮定するとP→Q→Rという三段論法(syllogism)によりRが演繹され、①∧not①という矛盾が生じる。そこでPが偽であることが背理法によって結論されるため、( ②を真として受け入れた場合には)時間整合性が破れているのだろう、というロジックである。
--------------やや詳細な分析---------------------------------
ただし、ここまでのロジック操作のステップにおいては、Pから「時間整合性①かつ時間非整合性not①」という矛盾が得られただけなので、時間整合性を捨て去るべきなのか、それとも時間非整合性をすてさる(つまり時間整合性を捨てない)べきなのか、結論できない(「P⇒①∧not①」 が真であることが示せただけであり、①∧not①が真になるように①またはnot①を否定する必要があることが示せたわけではない。実際、①を否定しても、not①を否定しても、①∧not①を真にすることができない)。
ここで背理法を用いると、仮定したP(①∧②)が偽である、すなわち
not (①∧②)=(not ①) ∨ (not ②)
が成立ことが結論される。しかし、この段階でも、まだ時間整合性①を捨て去るべきなのか、効用関数の線形性②を捨て去るべきなのか、ということについては結論ができない。しかし、時間によらない消費行動が合理的であると仮定-------つまり、お金自体を人々は報酬として感じずに、お金を十分多種類の物やサービスに分散して消費し、富や所得水準を変化させてしまうほど大きな金額でなければ、限界効用が逓減しないように効率的に消費すると仮定-------すれば、②が真であると仮定できるので、Pに含まれる①という時間整合性が否定される、という論法である。
(ここで行ったロジック操作をもう少し詳しく分解してみると、Pから
P∧R:(①∧②)∧(not①)
という矛盾が演繹される(P⇒P∧Rが真である)からといって、Pに含まれている①を捨て去る必要があるとは限らない。すなわちPに含まれている②を偽として(こうするとPが偽になる)、Tが真であるにも関わらず③の式(Q)が演繹されないようにして(すると、Sが真であるにも関わらずRという時間非整合性も演繹されなくなる)矛盾が生じないようにしてもよいはずであるが、ミクロ経済学における部分均衡分析おいては、貨幣の効用は線形であると仮定(準線形効用の仮定、なぜなら貨幣は効用を引き上げる財ではないから)するので、②を真としたまま、「①が偽となることによってPが偽になっている」、とThaler1981は解釈しているわけである。仮に、一般均衡分析の枠組みで物事を考えている場合には、お金(貨幣)が出る幕がないので、実験の際には、各財そのものーーー消費可能なコーラや音楽の視聴時間などを、インセンティブとして用いた実験デザインにしないと、ロジック矛盾がデータ解析の際にたくさん生じてしまうであろう。したがって、標準的経済学の枠組みを仮定して実験を行う際に、お金がインセンティブとして採用されているのであれば、部分均衡分析の概念が用いられていると考えてよい。非標準的であるが政策応用などに用いられることがあるケインズ経済学の枠組み(流動性選好liquidity preferenceの存在を仮定する。流動性選好とは、貨幣保有が便益として選択される、という、貨幣の中立性を仮定する標準的経済学では合理的ではない選択に分類されるものである)で実験をデザインする際には、この限りではないが、その場合はIS-LM分析の変数などを用いてマクロ経済学(ニューケインジアンやポストケインジアン含む)の流動性に関するモデルの数式を用いたデータ分析を行わないと、ロジック矛盾が生じてしまう。)
(すなわち、人間の時間に関する合理性①を捨て去らずに、人間のお金の使い方やお金を欲しがる理由に関する合理性②のほうを否定することで実験結果を説明する、という時間非整合性の実在性に関する反論の余地がThaler1981による実験によっても残されたわけで、Thalerが1981論文で同時に報告しているu(x)が時間選好に与える効果:magnitude effectの考察を通じて、後のLoewenstein-Prelec theory 1992につながっていった。それに対して、Takahashi, 2005, Zauberman 2009などは、tに関する非線形変換の影響を考慮して、①を選択行動の上では否定、脳内情報処理においては肯定するモデル(人間は判断や意思決定を合理的に行っているが、判断材料の時間が歪んでいるために、非合理な選択行動をおこなってしまうというモデル)を提案し、実験的に確認をした。そのオリジナル論文の日本語解説はこちら)
----------------やや詳細な分析 ここまで-------------------------------
なお、双曲割引(hyperbolic discounting)の正確な概念定義は以下のリンク先を参照のこと。
Common Confusions over Hyperbolic Discounting
18 January 2008
Eric Rasmusen
※割引関数がD(t)=1/(1+kt)という特定の関数形のことは、「双曲割引関数」と行動経済学や行動分析学において呼ばれることがおおい(行動としての双曲割引hyperbolic discounting behaviorを記述する、多数存在するモデルたちの一つである。ほかにLaibsonらの準双曲割引関数 quasi hyperbolic functionなども、離散時間における動的なゲーム理論においてよく用いられる)。なお、ここで出てくるkは、双曲割引関数のDR(t)と、一般のt(>0)においては一致しない(計算してこのことを確かめてみよ)ので、双曲割引関数などにおいては、「kが時間割引率である」と誤解しないことが、データの解釈などにおいて重要である。
-----------------------------------------------------------------------------
レポート課題
自分で得たデータをもちいて、3本の割引曲線(指数関数モデルを用いたもの)を、縦軸にU(x,t),横軸にtをとって描画して、特徴を説明せよ。(以下のエクセルファイル左上のa,b,cの直下のセルに自分のデータを入力すれば、グラフが自動的に描画されるので、そのエクセルファイルも提出せよ)
おまけ1:また、余裕があれば、上記で説明したとおりのデータ解析を行ってグラフを描画した後に、「得られた3本の線が、この実験参加者の割引行動を表す3つの割引曲線たちです」、と仮に結論した場合(もちろんRichard Thalerはそのようなデータ解釈の誤りを元論文で犯していないけれども)、そのデータの解釈方法がどのような論理的誤謬(logic fallacy)になってしまっているか、考察せよ。また、同様の誤謬の例であるが、Thaler 1981の1500円の場合には、3つのDRの直線回帰による近似式がDR=-0.7t+2.6となる(tは年単位)が、このデータセットの時間割引を記述するモデルとしてU(1500,t)=1500exp(-[-0.7t+2.6] t)としてしまうと、このモデルにはどんな数学的誤謬が生じるか(ヒント:DRの定義から計算したものと、カッコ内の太字の式が一致するか?)→答えはこちらのリンク
(データ解析をする際に、意味を理解しないまま、機械的に式に数値をあてはめてコンピュータを操作してグラフを描いてみたら、ちゃんと予想通りの出力がでてきたということから、データ解析の意味内容を理解できているのだろう、と勘違いしまっていないかどうかのチェック。データ解析をおこなった際には、いったん、自分が何を行っていたのかを正確に理解しているのかどうかチェックを行わないと、データ解析手順が正しくても、間違った結論にたどりついてしまうため、しばしばこのようなチェックが必要である。)
(ヒント:たとえば双曲割引関数U(x,t)=U(x,0)/(1+kt)をフィッティングして同様のデータ解析を行った後にーーーーおそらくは1本に重ならず、3本得られるはずであるがーーー「得られた3本の線が、この実験参加者の割引行動を表す割引曲線たちです」と結論するのは、このような論理的誤謬を引き起こさない。)
(謝辞:また、時間選好と将来の不確実性・リスクへの選好との関係について、はじめてこの話題にふれる学生さん方は興味をもちそうですね、と福井県立大学・佐野一雄先生(ファイナンス)にご議論いただき、金利の期間構造に関するBlack-Derman-Toyモデルに関して情報提供いただきました。この点については、我々の以前の研究(報酬が将来受け取れることの主観確率の時間変化の測定):
により、将来の主観的リスクと時間選好との関連が調べられています。この論文では、将来のリスクが不確定な状況に直面している生物の行動に関する進化論的な時間選好理論を検証しています)
---------------------------------------------------------------------------
(補足)
例:時間割引率が0.05の場合fooplot.com
で
1500*exp*(-0.05*x)をxが0から200、yが0から1500の範囲でグラフ描画すると以下のようになる(このオンライングラフ描画サイトの性質上、x軸がt、y軸が割引効用Uである)。

この例の0.05の代わりに、a, b,cから
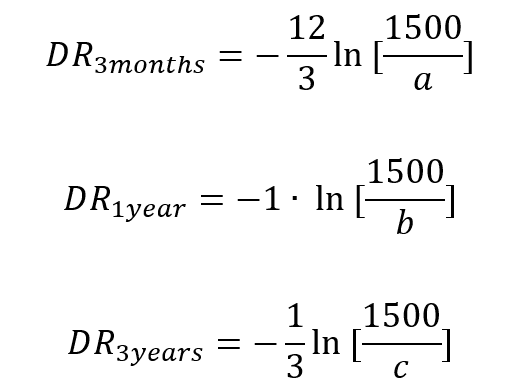
を用いて求められた相異なる3つのDRの数字を代入してグラフを3本描画すればよい。
たとえばa=3000であれば、以下のようにGoogle入力すれば時間割引率2.77....が求まる。(Thaler 1981の原論文では、277%と100倍された数値が報告されている)

参考:
時間選好におけるナッジの説明は以下を参照(ただし初心者には難解)
時間非整合性について一般向けに経済学者が解説した本
自滅する選択―先延ばしで後悔しないための新しい経済学 (日本語) 単行本 – 2012/5/18
池田 新介 (著)
(池田先生よりご恵贈いただきました)
出版社 : 東洋経済新報社 (2012/5/18)
発売日 : 2012/5/18
言語: : 日本語
単行本 : 284ページ
ISBN-10 : 4492314229
ISBN-13 : 978-4492314227

「経済セミナー」(日本評論社)において、行動経済学会・室岡健志先生により、異時点間選択の解説が行われています:
経済セミナー連載(2019年10・11月号よりスタート)
室岡健志「行動経済学:人の心理を組み入れた経済理論」
ウェブ付録・特設サイトのご案内
https://www.nippyo.co.jp/blogkeisemi/available_support_guide/murooka_behavioralecon/
時間非整合性について一般向けに精神医学者が解説した本
誘惑される意志 人はなぜ自滅的行動をするのか (日本語) 単行本 – 2006/8/30
ジョージ・エインズリー (著), 山形 浩生 (翻訳)
出版社 : NTT出版 (2006/8/30)
発売日 : 2006/8/30
言語: : 日本語
単行本 : 416ページ
ISBN-10 : 4757160119
ISBN-13 : 978-4757160118

時間割引とセルフコントロールについて、神経経済学、医療、臨床心理学、行動分析学など多方面からの解説が学べる本
セルフ・コントロールの心理学:自己制御の基礎と教育・医療・矯正への応用 (日本語) 単行本(ソフトカバー) – 2017/6/9
高橋 雅治 (著, 編集), 佐伯 大輔 (著), 井垣 竹晴 (著), 杉若 弘子 (著), 伊藤 正人 (著), 空間 美智子 (著), 平岡 恭一 (著), 青山 謙二郎 (著), 高木 悠哉 (著), 飛田 伊都子 (著), 鎌倉 やよい (著), 百瀬 由美子 (著), 深田 順子 (著), 坂上 貴之 (著), 蒲生 裕司 (著), 高橋 泰城 (著), 池上 将永 (著)

