
ベルヌーイ試行と二項分布
ベルヌーイ試行と二項分布
ベルヌーイ試行とは
まず、「ベルヌーイ試行」というのは、何を指すのでしょうか。これは、結果が2つの可能性しかないような試行のことを言います。
例えば、コインを投げることを考えてみましょう。コインを投げると、結果は「表」か「裏」の2つだけですよね。これがベルヌーイ試行の一例です。また、サイコロを振って「6が出る」か「6以外が出る」かを考えるのも、ベルヌーイ試行です。
二項分布とは
次に「二項分布」について説明します。二項分布は、ベルヌーイ試行をたくさん繰り返したときに、どのくらいの回数で「成功」(たとえばコインで言えば「表が出る」こと)が起きるかを調べるための方法です。
二項分布を理解するために、再びコインを投げることを考えてみましょう。コインを一回投げて「表」が出る確率は1/2ですよね。でも、もしコインを10回投げたら、「表」は何回出るでしょうか?それが分かるのが二項分布なんです。
つまり、「表が3回出る確率はどれくらい?」、「表が5回出る確率はどれくらい?」といったことを計算するのが二項分布です。
ベルヌーイ試行とは「結果が2つだけ」の試行のことで、コインを投げることや、サイコロで「6が出るか出ないか」を考えることなどが例です。そして二項分布は、このベルヌーイ試行をたくさん繰り返したときに、「成功」が何回起きるかを調べる方法です。
ベルヌーイ試行と二項分布:詳しい解説
ベルヌーイ試行とは 少し詳しく
「ベルヌーイ試行」とは結果が二つだけの試行のことを指します。例えば、コイン投げでは「表」と「裏」の2つの結果があります。これをベルヌーイ試行と呼びます。サイコロで「6が出る」か「6以外が出る」の二つを考えるのもベルヌーイ試行です。
二項分布とは 少し詳しく
次に「二項分布」について説明します。二項分布は、ベルヌーイ試行をn回繰り返したときに、「成功」(例えばコインでいう「表が出る」こと)がx回起きる確率を求めるものです。つまり、n回の試行中でx回成功する確率です。
具体的な式
二項分布の確率は以下の式で表されます。

ここで、
P(X=x) は、「n回の試行中にx回成功する確率」を意味します。
nCx は、「n回の試行からx回の成功を選ぶ組み合わせ」を表します。これは数学的に「nのxへの組み合わせ」と言います。
p は「1回の試行で成功する確率」で、コイン投げの例だと1/2になります。
(1-p) は「1回の試行で失敗する確率」で、コイン投げだとこちらも1/2になります。
具体的な例
具体的な例として、コイン投げを考えてみましょう。コイン投げの結果は「表」か「裏」で、それぞれの確率は1/2です。
ここで、このコインを10回投げたときに「表」が3回出る確率を求めてみましょう。これは上記の式を使って計算することができます。
nは10(試行回数)になります。
xは3(成功する回数)になります。
pは1/2(成功する確率)です。
これらの値を上記の二項分布の式に代入すると、「10回のコイン投げで表が3回出る確率」が求まります。
上記の例の値を式に代入すると以下のようになります。

まず、10C3を計算します。これは10から3を選ぶ組み合わせの数で、結果は120です。
次に、(1/2)^3 を計算します。これは表が出る確率を3回掛けたもので、結果は1/8です。
最後に、(1/2)^(10-3) を計算します。これは裏が出る確率を7回掛けたもので、結果は1/128です。
これらの値を全て掛け合わせると、「10回のコイン投げで表が3回出る確率」が求まります。計算すると、その確率は約0.117となります。
以上がベルヌーイ試行と二項分布の説明です。ベルヌーイ試行は2つの結果を持つ試行、そして二項分布はその試行をn回繰り返したときの「成功」の回数の確率を求めるものとなります
ポアソン分布
二項分布における (試行回数n) が十分大きく、(確率p)が非常に小さい場合、現象が起こる回数Xはポアソン分布に従うと考えられます。
ポアソン分布はまれな現象の大量観測と捉えられます。
ポアソン分布は、一定の期間または範囲で平均的に起こる回数を知っているイベントが、特定の期間または範囲で実際に何回起こるかの確率を計算するためのものです。
想像してみてください、あるお菓子屋さんがあります。このお店では平均的に1時間に3人のお客さんが来ます。では、次の時間で5人のお客さんが来る確率はどれくらいでしょうか?これがポアソン分布で解くことができる問題です。
数式では以下のように表されます
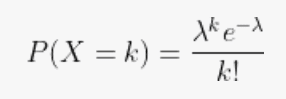
ここで、
λ (ラムダ)は平均発生回数 (この場合、1時間当たりのお客さんの平均数)
kは求めたい回数 (この場合、5人)
eは自然対数の底(約2.71828の定数)
k!(kの階乗)はk*(k-1)(k-2)...*1 の積
です。
このお店の場合、λ=3, k=5 を上記の数式に入れて計算すると、次の時間に5人のお客さんが来る確率が求まります。
このようにポアソン分布は、
「普通はここにこういう数が来るんだけど、じゃあ今回は何人来るかな?」というような問いに答えるのに役立つんですね!
ポアソン分布の平均と分散
平均(期待値)
ポアソン分布の平均、または期待値は、λ(ラムダ)です。これはポアソン分布を定義するときに使われるパラメータで、一定の期間または空間で平均的に起こるイベントの回数を表します。
例えば、ある公園で平均して1時間に5回鳥が飛んでくるとすると、これをポアソン分布で表すときのλは5になります。これは「平均的に1時間に5回鳥が飛んでくる」という情報を表しています。
分散
ポアソン分布の分散もまたλです。分散はデータが平均値からどれだけばらついているかを示す値です。ポアソン分布では、平均値と同じくλがこのばらつきを決定します。
これはポアソン分布が一つのパラメータ、λによって特徴付けられるという性質を反映しています。つまり、イベントが平均的にどれくらいの頻度で起きるか(平均=λ)だけでなく、それがどれくらいばらつくか(分散=λ)も同時に決まるのです。
以上、ポアソン分布の平均と分散についての説明でした。平均と分散が同じ値(λ)で決まるというポアソン分布の特性を覚えておくと、データの分析がさらに進みますよ!
