
○○のグラフはチャートにそっくり
トレードとチャートは切っても切り離せない関係です。
チャートを見てラインを引いたりパターン認識をするのが通常です。
でもテクニカルチャートって、乱数の対数変化をグラフ化したものにそっくりなんです。
乱数=出現する値に規則性のない数 となります
そのランダムな変化の対数を折れ線グラフ化すると、、


何のチャートですか?というグラフになります。
全ての乱数の出現率は一緒
つまりは上がるも下がるも1/2
上昇幅と下落幅を足せば0になる可能性が一番高い関数が描くチャートです。
つまり、そこにあるのは1/2の確率が合わさって出来上がったもの。
「そこに意味はない」
こんなラインを引いても

ヘッド&ショルダーやその戻りやブレイクを見つけても

偶然が描き出すものに、意味を見ているだけ
ということになります。
エンターキーを押すごとに、チャートは色々形を変えます。



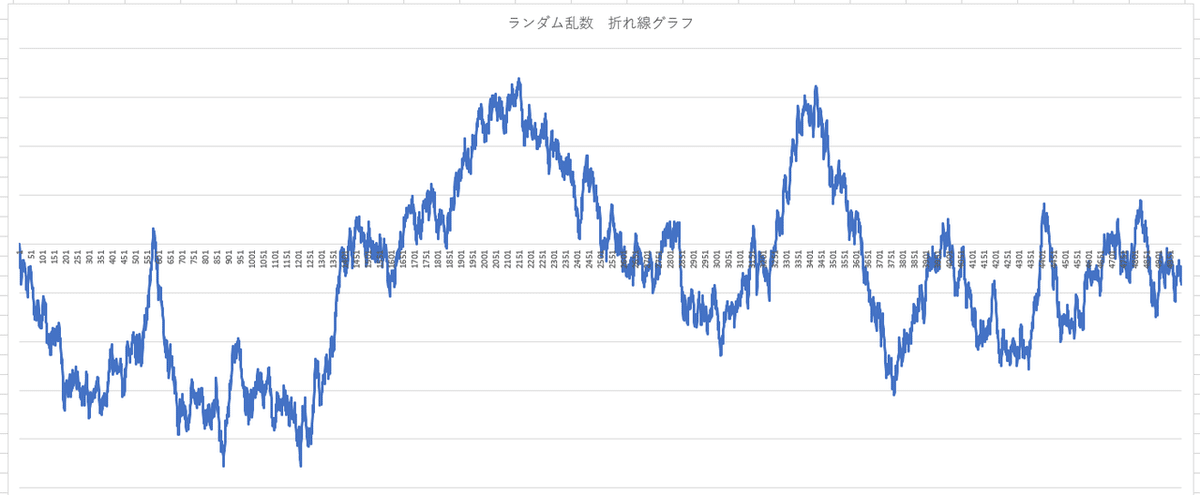
全て、期待値はゼロの乱数から発生したグラフです。
「ランダム(乱数)だと色んなパターンは現れない」
という考えをたまに見るのですが、思ってる以上に様々な形を描きます。
そして、
トレンドライン
チャネルライン
抵抗ライン
ヘッド&ショルダーズ
ダブルトップ
ダブルボトム
上昇トレンド
下降トレンド
など色々書けますし言えますよねこれを見て。
でもただの期待値ゼロの乱数のグラフです。
次上がるか下がるかは50:50
上下量も全てを足すといずれゼロになる世界のグラフです。
乱数チャートが金融商品のチャートに似ているからといって、全てのテクニカル分析を無意味にできるものではありません、が、
実際の市場の世界ではおそらくたまたまの結果に
あれこれ理由付けて後付け分析がされているケースも多いだろうと推定してます。
この乱数チャートの価格変化率のヒストグラムはこうなります。

日経先物やドル円の価格変化率のヒストグラムはこうなります。


似てますね。8割ほどは似てますが、若干は違います。
金融商品の方が裾野が広い。
金融商品の方が裾野が広くなるのは、行動ファイナンス論が関係してくるからかと思われます。
つまり「人間の感情は走るから」ということですね。
乱数との諸々の相関性から、金融市場のランダム性が類推できると同時に、また違いも存在していることが認識できます。
対象が主にデリバティブなのか、マネーが投入される株式市場等なのかで結果も若干変わってきますね。
今回の記事で使用したランダムウォークのエクセルファイルをDL頂けます。
一番左上のセルの中に入って、数式をいじらずにエンターキーを押せば、チャートが形を変えていきます。
ランダムである乱数がどれほど現実に近いチャートを描くか、お楽しみ下さい^^
いいなと思ったら応援しよう!

