分割表の検定でわかること

２ｘ２分割表は、数字が4つ並んだものです。これを使った検定の例を紹介してみます。起きていることが、偶然なのかを判定します。

以下は、新型コロナウイルスの後遺症の研究に使われた統計データについてで紹介した例です。

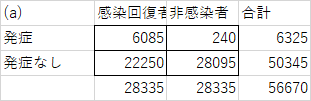
規呼吸器系疾患がなかった人が条件で、新型コロナ発症＆回復者と、感染なしの人について、ある期間で新規に規呼吸器系疾患に発症した人がどのくらいいたか、という比較です。（条件を揃えての比較）

感染回復者と非感染者の合計人数が同じなので、一目瞭然、回復者の方が新規発症が極端に多くなっていることは、すぐにわかります。わかりますが、どのように計算すれば「多くなっている」と結論できるのでしょうか。どの位多い場合に、違いがあると判断できるのでしょうか？

例えばこちらの(b)ような数字だったら？（以下の分割表の数字は説明のための数字になっています）

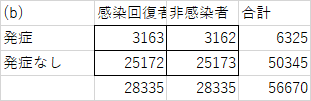
一人だけの違いですから、偶然の可能性が高いですね。

次の(c)の場合は、少し差が大きくなっています。

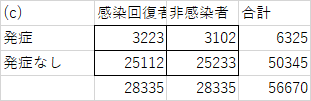
この例では、10回に1回位はこのくらいのばらつきがあり得るという計算結果になりました。比較的頻度は高いので、(b)と同様に偶然だろうと判断します。

次の(c)はさらに微妙です。差が開いているので、偶然起きる確率は低くなります。

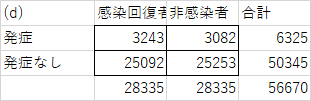
そして差がひらくほど、偶然に起きる確率は低くなります。計算すると、100回に3回程度の確率になります。

100回に3回を偶然起きることと判断するのか、めったに起きないことと考えるのか。

これは、実は予め決めておく必要があります。

仮説検定では、先にどの範囲なら採択するか（偶然起きたと判断する条件）を決めておきます。これを有意水準と言います。そして帰無仮説をたてます。この例では、「感染回復者と非感染者は、新たに呼吸器系疾患を発症する頻度は同じ」となります。あらかじめ決めて置いたこの有意水準を元に、帰無仮説が偶然起きるかどうかを判断します。

ちなみにこの(d)の例で、有意水準を0.05としていた場合には、帰無仮説は棄却され、この結果はめったに起きないことだ、感染回復者と非感染者では呼吸器系疾患を発症する頻度は同じではない、新たに呼吸器系疾患を発症する頻度は異なる、と判断されます。

一方有意水準を0.01としていた場合には、「感染回復者と非感染者は、新たに呼吸器系疾患を発症する頻度は同じ」が否定されません。偶然起きた可能性がある、と理解されます。これを採択と呼びます。同じ可能性もあるし、違う可能性もある、という意味になります。「同じ」とは解釈されないことに注意しましょう。

さて、(d)では微妙でしたが、(a) はもっとずっと確率が低くなります。計算するまでもなく、違いはある、と判断して良いでしょう。

分割表という単純な表であっても、期待度数（今回は(b)に近い表）を計算し、比較をすることによって、定量的にデータを読み解くことができる訳です。これはノンパラメトリック検定の1例です。

（仮説検定については、「帰無仮説」「棄却域」「ｐ値」などのキーワードの説明を探してください。そしてこの例は、仮説検定のうち、独立性の検定の簡単な説明となっています。）