偏差値とは何か
こんなに恥ずかしいタイトルの記事は初めて見ました。「日本人の6人に1人は偏差値40以下、5人に1人は役所の書類を申請できない…“見えない格差”をつくった知識社会のザンコク」

信じられない。偏差値が何かを意味するかを知らない人?(本文を見ると知っているようでもあり。。。)
それでもこのようなタイトルで記事を書いていると思うと、日本の知的レベルの劣化の実例を見る思いがします。
では、このタイトルの何がおかしいのかを簡単に説明しようと思います。
その前提として、正規分布が重要です。式や本来は連続関数であることはともかく、こんな形になります。
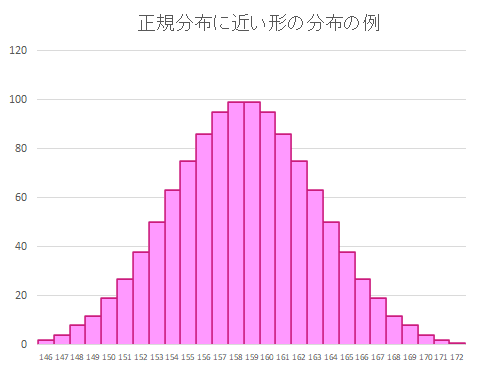
この形の分布になるものは、とても多いのです。例えば「学校保健統計調査 / 令和2年度 全国表 」でも17歳男女の身長の分布もこんな風になります。

面白いのは、例えば生徒毎に複数の学科のテストの平均点を計算し、多くの生徒の平均点のヒストグラムを作成すると、人数を増やすことでやはり正規分布に近づいていきます。
例えば身長170cmは、女性では平均よりかなり高いことがわかります。しかし男性では平均的な高さです。同じ身長でも、女性か男性かで背が高いのかそうでもないのかが変わるわけです。
これを数値で比べる場合は、この分布の形が正規分布に近いことを想定(利用)して行います。具体的には平均と分散(ばらつき具合、標準偏差の2乗)で計算できます。この例では、
女性の身長の平均=157.9cm 女性の身長の標準偏差=5.4cm
男性の身長の平均=170.7cm 男性の身長の標準偏差=5.8cm
となっています。計算すると、女性170cmの人は、平均よりも標準偏差の2.26倍高く、男性ならば平均よりも標準偏差の0.11倍低くなります。女性の2.26倍という数字から、分布が正規分布であれば、170cm以上の身長の人はおよそ100人に一人程度しかいないことがわかります(正規分布表から読み取れます)。
女性の170cmの人の割合と、男性184cmの人の割合はほぼ同じになります。感覚的に比較的高い人だな、という意味で直感にあっていますね。
実はこの説明には2つの事実を使っています。
・異なる正規分布も、その平均と分散がわかれば比較できる
・正規分布の時、その平均と分散(または標準偏差)がわかっていれば、ある値がどの程度珍しいのか数値化できる
テストの平均点が正規分布であるとの仮定の元(そして実際にデータが多い場合には正規分布に近づく)、「偏差値」はこれを使って平均点を50、標準偏差を10とした値に変換したものです。(「偏差値」は日本でのみで利用されていると聞きました。)例えば以下のテストの点数分布を偏差値に変換した結果を示します。
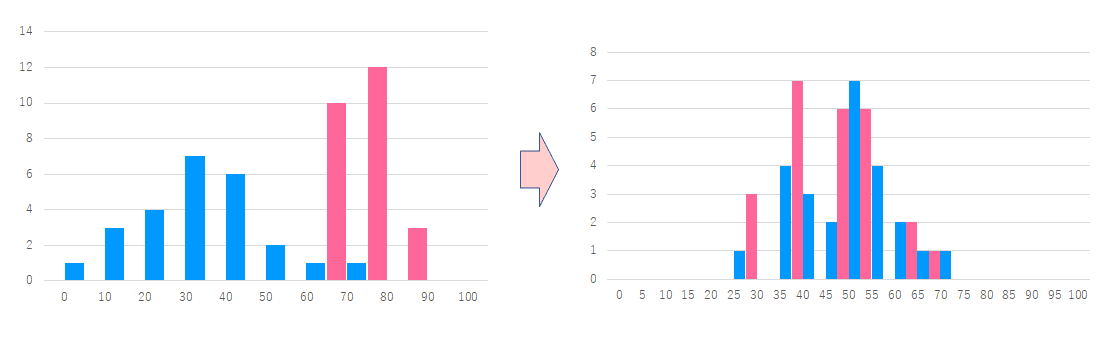
標準偏差に変換させることで、テストの難しさを考慮した相対比較ができるようになります。
そして正規分布は、数値計算によって、ある範囲に含まれる割合がわかっています。統計を学んだ人なら、平均±1.96σの範囲に95%のデータが入ることを必ず学びます(σは標準偏差)。同様に、平均±σの範囲に68.26%、実に2/3以上が入ってきます。そしてその範囲から外れるのは、右側が1/6弱、左側も1/6弱になります(それぞれ15.87%)。

これらの結果から言えるのは、標準偏差40以下になるのは、16%弱であること。そうなるように定義されている、ということです。
ここまでくれば、「日本人の6人に1人は偏差値40以下」のおかしさの意味がわかります。1/6は約16.7%です。確かに15.87%は近い値です。しかしそもそもの定義で、相対的に必ず約16%の人が偏差値40以下になるように計算されたものが偏差値です。
「日本人の6人に1人は偏差値40以下」なのはあたりまえ。そう定義されているとしか言いようがありません。
さて、本文を見ると、
正規分布では、平均(偏差値50)から1標準偏差離れた、偏差値40~60の範囲に68・3%の事象が収まる。2標準偏差離れた偏差値60~70と30~40はそれぞれ13・6%、3標準偏差離れた偏差値70~80と20~30はそれぞれ2・15%だ。
との記載があり、一応わかっている?
なのにこのタイトルを選んだ?
(少し修正しました。分散=標準偏差の2乗)
