画像解析を高速化させるためのTipsわかりやすくまとめてみた(3)

前回（第2回）は、固定小数点数の話をしました。固定小数点数を使った整数型演算で、割り算を使わない割り算の方法を説明しました。

今回は、前回説明した、割り算を使わない割り算を用いて、前々回（第1回）の整数型での四捨五入を、SIMDの整数型で計算する方法を説明します。

SIMDとは

Single Instruction, Multiple Data の略で、1つの命令で複数のデータに対して同時に並列に演算する手法です。ベクトル演算とも呼ばれます。SIMD命令があるプロセッサには、例えば、下の図のように、8個の数値のデータ列2つを1命令で足し算できます。SIMD命令を用いることで、計算処理の高速化ができます。

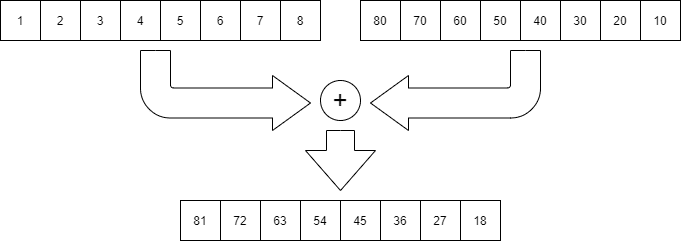
IntelのSIMD

プロセッサの進化するにしたがって、SIMDも進化していきました。Intelの場合は、ざっくりと以下のような感じです。

・MMX（64ビットレジスタ）
　・浮動小数点演算レジスタを転用、複数の整数を同時に演算
・SSE～SSE4.2（128ビットレジスタ）
　・SSE：単精度浮動小数点演算
　・SSE2：倍精度浮動小数点演算、整数演算
　・SSE3：メモリアクセス高速化、複素数計算高速化
　・SSSE3：水平加算など
　・SSE4.1：丸め計算など
　・SSE4.2：文字列用命令、CRC-32など
・AVX～AVX2（256ビットレジスタ）
　・AVX：浮動小数点演算
　・AVX2：整数演算
・AVX-512（512ビットレジスタ）

SSE, AVX拡張命令は、C言語から直接利用することもできます。
Intel Intrinsics Guide:
https://software.intel.com/sites/landingpage/IntrinsicsGuide/

割り算を使わない割り算のSIMD実装

では、おもむろに、前回やった割り算をつかわない割り算のSIMD実装です。

#include <immintrin.h>// __m128i を int32_t　の配列としてアクセスするための共用体
union m128i_i32
{
   __m128i m;
   int32_t i[4];
};

// 逆数テーブル クラス
template <int NumBits, int DenBits>
class InvTable
{
   int r[1 << DenBits] = {};
public:
   constexpr InvTable() {
       for (int i = 1; i < 1 << DenBits; ++i) {
           r[i] = (1 << (NumBits + DenBits)) / i;
       }
   }
   constexpr int operator[](int n) const {
       return r[n];
   }
};

constexpr int NUM_BITS = 9;     // 分子のビット数
constexpr int DEN_BITS = 8;     // 分母のビット数

// 逆数テーブル
constexpr auto inv_table = InvTable<NUM_BITS, DEN_BITS>();

// 割り算 (int32_t の __m128i)
inline __m128i div_int_sse2(__m128i mx, __m128i my)
{
   auto a = reinterpret_cast<m128i_i32*>(&my);

   // (1)
   __m128i mr = _mm_set_epi32(
       inv_table[a->i[3]], inv_table[a->i[2]],
       inv_table[a->i[1]], inv_table[a->i[0]]);

#if __SSE4_1__
   // (2)
   __m128i mc = _mm_mullo_epi32(mx, mr);

#elif __SSE2__
   __m128i mc_even = _mm_mul_epu32(mx, mr);
   __m128i mc_odd  = _mm_mul_epu32(
       _mm_shuffle_epi32(mx, 0xb1), _mm_shuffle_epi32(mr, 0xb1));
   __m128i mc_mask = _mm_set_epi32(0, -1, 0, -1);
   __m128i mc = _mm_or_si128(
       _mm_and_si128(mc_mask, mc_even),
       _mm_andnot_si128(mc_mask, _mm_slli_si128(mc_odd, 4)));

#endif
   // (3)
   __m128i md = _mm_add_epi32(mc, _mm_set1_epi32(1 << NUM_BITS));
   // (4)
   __m128i me = _mm_srli_epi32(md, NUM_BITS + DEN_BITS);
   return me;
}

__m128i という型が SSE2 の命令で使用するデータ型で128ビット（16バイト）のサイズがあります。この型の変数にデータを入れて、前項のリンクにある Intrinsics の組み込み命令を呼べばOKです。今回は、32ビット整数で計算するので、4個の整数を同時に計算することになります。

(1) _mm_set_epi32: 4個の32ビット整数をパックして __m128i 型に入れます。
ここでは、逆数テーブルから値をピックアップして用意しています。
※逆数のテーブルは、constexpr にしてコンパイル時に計算させています。

(2) _mm_mullo_epi32: 4個の32ビット整数を同時に掛け算します。この命令はSSE4.1の命令なので、SSE2で同じことをする場合は、他の命令を組み合わせて実現します。
ここでは、｛割られる数｝と｛割る数の逆数｝を掛け算しています。

(3) _mm_add_epi32: 4個の32ビット整数を同時に足し算します。
ここでは、誤差の補正をしています。

(4) _mm_srli_epi32: 4個の32ビット整数を同時に右シフト演算します。
ここでは、固定小数点の小数部を切り捨てています。

整数型での四捨五入のSIMD実装

次に、前々回やった整数型での四捨五入のSIMD実装です。

// int型 sse2版
void div_round_int_sse2(
   const __m128i* px, const __m128i* py, __m128i* pans)
{
   // (1)
   __m128i mx = _mm_load_si128(px);
   // (2)
   __m128i my = _mm_load_si128(py);
   // (3)
   __m128i ma = _mm_srli_epi32(my, 1);
   // (4)
   __m128i mb = _mm_add_epi32(mx, ma);
   // (5)
   __m128i mans = div_int_sse2(mb, my);
   // (6)
   _mm_store_si128(pans, mans);
}

(1) _mm_load_si128: メモリからレジスタにデータをロードします。この命令を使う場合は、16バイトでアラインメントを合わせる（16で割り切れるアドレスを指定する）必要があります。アラインメントされていないメモリからロードする場合は、_mm_loadu_si128 や _mm_lddqu_si128（SSE3）を使用できますが、_mm_load_si128 と比べると速度は遅くなります。
ここでは、割られる数をレジスタにロードしています。(x)

(2) 割る数をレジスタにロードしています。(y)

(3) 右シフト演算することで、割る数を1/2しています。(y >> 1)

(4) (x + (y >> 1))

(5) 前項の割り算をつかわない割り算の関数を呼び出しています。

(6) _mm_store_si128: メモリにレジスタの値をストアします。この命令を使う場合も、16バイトでアラインメントを合わせる必要があります。アラインメントされていないメモリへストアする場合は、_mm_storeu_si128 を使用できますが、_mm_store_si128 と比べると速度は遅くなります。

ベンチマーク

前々回と実行時間を比較してみましょう。

//! @file: benchmark.cpp

#include <iostream>

#include <chrono>

#include <immintrin.h>

// ベンチマーク
void benchmark_sse2(
   void (*func)(const __m128i* x, const __m128i* y , __m128i* ans),
   int n, const int* x, const int* y, int* ans)
{
   auto start = std::chrono::system_clock::now();
   // ここから

   for (int i = 0; i < n; i += 4) {
       func(reinterpret_cast<const __m128i*>(&x[i]),
           reinterpret_cast<const __m128i*>(&y[i]),
           reinterpret_cast<__m128i*>(&ans[i]));
   }

   // ここまで
   auto end = std::chrono::system_clock::now();
   auto elapsed = std::chrono::duration_cast<std::chrono::milliseconds>(end - start).count();
   std::cout << elapsed << std::endl;
}

//! @file: main.cpp

#include <vector>

#include <random>

#include <algorithm>

#include <immintrin.h>

#include <iostream>

#include <memory>

#include "aligned_allocator.h"

// int型 sse2版
void div_round_int_sse2(
   const __m128i* x, const __m128i* y , __m128i* ans);

// ベンチマーク
void benchmark(int (*func)(int, int), int n,
   const int* x, const int* y, int* ans);
void benchmark_sse2(
   void (*func)(const __m128i* x, const __m128i* y , __m128i* ans),
   int n, const int* x, const int* y, int* ans);

int main()
{
   static const int N = 10000000;

   std::random_device rd;
   std::mt19937 mt(rd());
   std::uniform_int_distribution<> rand256(1, 255);

   std::vector<int, aligned_allocator<int, 16>> x(N);
   std::vector<int, aligned_allocator<int, 16>> y(N);
   std::vector<int, aligned_allocator<int, 16>> ans1(N);
   std::vector<int, aligned_allocator<int, 16>> ans2(N);
   std::vector<int, aligned_allocator<int, 16>> ans3(N);
   std::generate(x.begin(), x.end(), [&](){ return rand256(mt); });
   std::generate(y.begin(), y.end(), [&](){ return rand256(mt); });

   benchmark_sse2(div_round_int_sse2, N,
       x.data(), y.data(), ans3.data());

   return 0;
}

アラインメントを16バイトに合わせるため、std::aligned_alloc という C++17 から使用できるアラインメントされたメモリを確保する関数を使用します。C++17より前の場合は、処理系固有の同様の関数を使用します。この関数を std::vector で使用するため、アロケータを定義しました。

//! @file: aligned_allocator.h

#pragma once

#include <cstdlib>

template <class T, int N>
class aligned_allocator
{
public:
   typedef size_t size_type;
   typedef ptrdiff_t difference_type;
   typedef T* pointer;
   typedef const T* const_pointer;
   typedef T& reference;
   typedef const T& const_reference;
   typedef T value_type;

   template <class U>
   struct rebind { typedef aligned_allocator<U, N> other; };

   aligned_allocator() throw() {}
   aligned_allocator(const aligned_allocator&) throw() {}
   template <class U>
   aligned_allocator(const aligned_allocator<U, N>&) throw() {}
   template <class U>
   aligned_allocator<T, N>& operator=(const aligned_allocator<U, N>&) {
       return (*this);
   }

   ~aligned_allocator() throw() {}

   pointer allocate(size_type num, const void* /*hint*/ = 0) {
       return static_cast<pointer>(
           std::aligned_alloc(N, (num * sizeof(T) + (N - 1)) & ~(N - 1)));
   }

   void deallocate(pointer p, size_type /*num*/) {
       std::free(p);
   }

   void construct(pointer p, const T& value) { new (p) T(value); }
   void destroy(pointer p) { p->~T(); }
   pointer address(reference value) const { return &value; }
   const_pointer address(const_reference value) const { return &value; }

   size_type max_size() const throw() {
       size_type count = (size_type)(-1) / sizeof(T);
       return (0 < count ? count : 1);
   }

};

template <class T, class U, int N>
bool operator==(const aligned_allocator<T, N>&,
    const aligned_allocator<U, N>&) throw() { return true; }

template <class T, class U, int N>
bool operator!=(const aligned_allocator<T, N>&,
    const aligned_allocator<U, N>&) throw() { return false; }

実行環境：
・CPU: 8th Generation Core i7
・OS: Ubuntu (WSL2)
・Compiler1: gcc version 7.5.0 (Ubuntu 7.5.0-3ubuntu1~18.04)
・Compiler2: clang version 6.0.0-1ubuntu2
・Compile Options: -O3 [ -msse4.1 | -msse2 ]

ベンチマーク結果（5試行平均）：

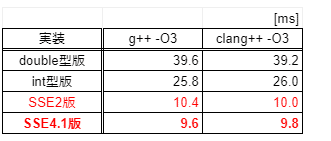
SSE4.1版は、int型版と比べて約2.7倍、double型版と比べて約4.1倍速くなりました。やったね！

今回は、4個の32ビット整数の並列演算でやりましたが、8個の16ビット整数で並列演算したり、AVXで実装すれば、さらに高速化ができます！

メンバー募集中です
アダコテックは上記のような画像処理技術を使って、大手メーカーの検査ラインを自動化するソフトウェアを開発している会社です。
機械学習や画像処理の内部ロジックに興味がある方、ご連絡下さい！
我々と一緒にモノづくりに革新を起こしましょう！

株式会社アダコテック