【Pyxel】Pyxelで学ぶゲーム数学の基礎〜距離の計算と当たり判定

今回は、レトロゲームエンジン「Pyxel」を使って、ゲームでよく使われる数学について学ぶ記事となります。

今回の内容は以下のもので、かなり基本的なものとです。

* 2点間の距離を求める方法
* 円同士の当たり判定
* 矩形同士の当たり判定

ですが、どれもゲームプログラムには必須の知識となります。
なお Pyxel のセットアップについては、以下のページにまとめていますので、まだインストールできていない場合は、こちらを参考にしてください。
【関連記事】：【Pyxel】セットアップ手順と基本の関数について

■2つの円を描くプログラムの作成

まずは Pyxel を動かすための最小限のコードを書きます。

import pyxel

class App:
    def __init__(self):
        pyxel.init(160, 120, fps=60)
        pyxel.run(self.update, self.draw)
    
    def update(self):
        pass

    def draw(self):
        pass

App()

このコードを "main.py" などの名前で保存します。そうしたらコマンドプロンプト、もしくはターミナルから「python3 main.py」を実行して真っ暗な画面を表示します。

無の空間

ここに円を表示します。コードを以下のように修正します。

▼修正点
* class App の下に、円のサイズ（半径）の数値を追加
* __init__() に変数の初期化を追加
* update() にマウス移動の処理を追加
* draw() に円を描画する処理と円の座標を描画する処理を追加

import pyxel

class App:
    # サイズ定義
    SIZE1 = 8
    def __init__(self):
        pyxel.init(160, 120, fps=60)
        # 変数初期化
        self.x1 = pyxel.mouse_x
        self.y1 = pyxel.mouse_y
        pyxel.run(self.update, self.draw)
    
    def update(self):
        # マウスで移動する
        self.x1 = pyxel.mouse_x
        self.y1 = pyxel.mouse_y

    def draw(self):
        pyxel.cls(0)
        # 円を描画する
        pyxel.circ(self.x1, self.y1, self.SIZE1, 9)
        # 座標を描画する
        pyxel.text(0, 0, "ORANGE: %d,%d"%(self.x1, self.y1), 9)

App()

実行すると、オレンジの円が表示され、マウスカーソルで位置を移動できます。
左上には、円が存在する座標が文字として表示されます。

続けてもう１つ、円を描画するようにします。この円はキーボードで操作できるようにします。

▼修正点
* class App の下に、円のサイズ（半径）の数値を追加
* __init__() に変数の初期化を追加
* update() にキーボード移動の処理を追加
* draw() に円を描画する処理と円の座標を描画する処理を追加

import pyxel

class App:
    # サイズ定義
    SIZE1 = 8
    SIZE2 = 12
    def __init__(self):
        pyxel.init(160, 120, fps=60)
        # 変数初期化
        self.x1 = pyxel.mouse_x
        self.y1 = pyxel.mouse_y
        self.x2 = 30
        self.y2 = 30
        pyxel.run(self.update, self.draw)
    
    def update(self):
        # マウスで移動する
        self.x1 = pyxel.mouse_x
        self.y1 = pyxel.mouse_y
        # キーボード入力で移動する
        if pyxel.btn(pyxel.KEY_LEFT):
            self.x2 -= 1
        if pyxel.btn(pyxel.KEY_RIGHT):
            self.x2 += 1
        if pyxel.btn(pyxel.KEY_UP):
            self.y2 -= 1
        if pyxel.btn(pyxel.KEY_DOWN):
            self.y2 += 1

    def draw(self):
        pyxel.cls(0)
        # 円を描画する
        pyxel.circ(self.x1, self.y1, self.SIZE1, 9)
        pyxel.circ(self.x2, self.y2, self.SIZE2, 11)
        # 座標を描画する
        pyxel.text(0, 0, "ORANGE: %d,%d"%(self.x1, self.y1), 9)
        pyxel.text(0, 8, "GREEN: %d,%d"%(self.x2, self.y2), 11)

App()

実行すると少し大きな緑色の円が表示され、キーボードのカーソルキーで移動できます。

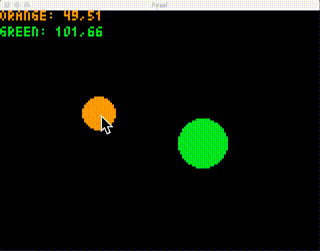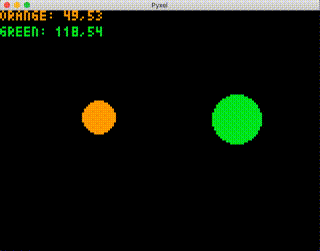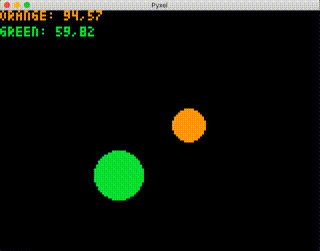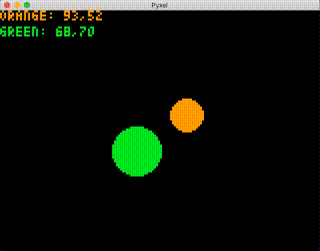
■2点の距離を求める

ここからが本番となります。2つの円の中心を結んだ距離を求めます。距離はゲームの様々な判定に使用することができる重要な概念です。

* プレイヤーが敵に近づいたら、敵がプレイヤーに気づく判定（一定の距離以下であれば敵がプレイヤーを追いかける、など）
* プレイヤーが遠くにいる場合は、敵は遠距離用の攻撃を仕掛けてくる
* 一番近くにいる敵を追いかけるホーミング弾の挙動を作る
* 円の当たり判定

なお、距離の計算は、ゲーム数学で必須となる「ベクトル」でも使用します。

では、距離を求めるための準備として、以下のコードを追加します。

    def draw(self):
        pyxel.cls(0)
        # 円を描画する
        pyxel.circ(self.x1, self.y1, self.SIZE1, 9)
        pyxel.circ(self.x2, self.y2, self.SIZE2, 11)
        # 座標を描画する
        pyxel.text(0, 0, "ORANGE: %d,%d"%(self.x1, self.y1), 9)
        pyxel.text(0, 8, "GREEN: %d,%d"%(self.x2, self.y2), 11)

        # 二点間を線でつなぐ
        pyxel.line(self.x1, self.y1, self.x2, self.y2, 7)

draw() に 2点の間を線でつなぐ pyxel.line() を入れました。実行してみると、円と円の中心を結ぶ線が引かれるようになります。この線の長さが二点間の距離となります。

距離を求めるための考えの基本は「引き算」となります。それは以下の図を見るとよくわかると思います。

この図を元に、A地点からB地点までの距離を求めるとどんな式になるでしょうか。

答えは、200 - 80 = 120 です。B地点 - A地点 でその区間の距離を求めることができます。

では、以下の図で、A地点(x, y) = (3, 2)からB地点(x, y) = (6, 6)の距離を求めるにはどうしたら良いでしょうか。（スクリーン座標系に合わせて、下方向をY軸のプラスとしています）

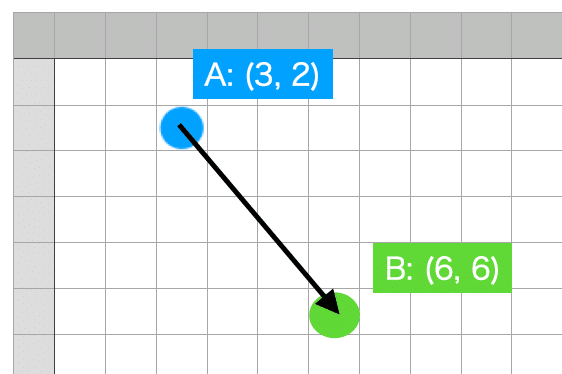
これも引き算の考えを利用します。BのXの値 "6" から AのXの値 "3" を引くと、"3"になり、AのYの値 "6" から "2" を引くと "4" になります。

そうすると、直角三角形の斜辺の長さは、三平方の定理により 底辺^2 + 高さ^2 をルートで割った値となります。距離は √(4*4 + 3*3) = √(16+9) = 5 ですね。

では、これをプログラムで実装してみます。まずはファイルの先頭に 平方根を計算するモジュールのインポート文 (import math) を記述します。

import pyxel
import math

class App:
    # サイズ定義
    SIZE1 = 8

そうしたら、draw() の最後に距離を計算する処理を記述します。

    def draw(self):
        pyxel.cls(0)
        # 円を描画する
        pyxel.circ(self.x1, self.y1, self.SIZE1, 9)
        pyxel.circ(self.x2, self.y2, self.SIZE2, 11)
        # 座標を描画する
        pyxel.text(0, 0, "ORANGE: %d,%d"%(self.x1, self.y1), 9)
        pyxel.text(0, 8, "GREEN: %d,%d"%(self.x2, self.y2), 11)

        # 二点間を線でつなぐ
        pyxel.line(self.x1, self.y1, self.x2, self.y2, 7)

        # 二点間の距離を求める
        dx = self.x2 - self.x1
        dy = self.y2 - self.y1
        distance = math.sqrt(dx*dx + dy*dy)
        pyxel.text(0, 16, "DISTANCE:%f"%distance, 7)

math.sqrt() を使用すると平方根の値を求めることができます。記述ができたら実行して動作を確認します。

操作は少し難しいですが、例えば円を (50, 50), (53, 54) の位置に配置すると、距離(DISTANCE)が "5" になるのを確認できると思います。

■円同士の当たり判定

距離の計算ができるようになると円同士の当たり判定が簡単に実装できます。
ちなみに当たり判定とは、2つのオブジェクトが接触しているかそうでないかを判定する処理となります。

例えば、シューティングゲームでは、自機に敵の弾が当たった時に、自機が爆発して消滅するというルールを採用しています。そういったルールを実装するには、当たり判定ができないと実装できません。
実は、先ほどの距離の計算ができている時点で、円同士の当たり判定は半分実装できています。

２つの円を近づけるとわかるのですが、２つの円、それぞれの半径を足したものが距離と一致した場合、２つの円が接触しています。
以下が、衝突しているかどうかを求める計算式です。

▼2つの円が衝突しているかどうか
距離の長さが２つの円の半径の合計よりも小さい
　＝ 距離 ＜ Aの半径 ＋Bの半径

ではこれをプログラムにしてみます。

    def draw(self):
        pyxel.cls(0)
        # 円を描画する
        pyxel.circ(self.x1, self.y1, self.SIZE1, 9)
        pyxel.circ(self.x2, self.y2, self.SIZE2, 11)
        # 座標を描画する
        pyxel.text(0, 0, "ORANGE: %d,%d"%(self.x1, self.y1), 9)
        pyxel.text(0, 8, "GREEN: %d,%d"%(self.x2, self.y2), 11)

        # 二点間を線でつなぐ
        pyxel.line(self.x1, self.y1, self.x2, self.y2, 7)

        # 二点間の距離を求める
        dx = self.x2 - self.x1
        dy = self.y2 - self.y1
        distance = math.sqrt(dx*dx + dy*dy)
        pyxel.text(0, 16, "DISTANCE:%f"%distance, 7)

        # 円での当たり判定
        if distance < self.SIZE1 + self.SIZE2:
            pyxel.text(0, 24, "HIT!", 7)

draw() の最後に円の当たり判定を追加しました。円が衝突していると "HIT!" という文字が表示されます。

■矩形同士の当たり判定

矩形同士の当たり判定は少し難しいので、まずは矩形と点の当たり判定から考えてみます。

黒い点(x, y) が、矩形内に存在するかどうかは、矩形の左上の点と右下の点の間に存在しているかどうかで判定できます。
プログラムでこれを実装します。

▼修正点
* 円の描画 pyxel.circ() を消して、矩形描画 pyxel.rect() を追加
* 円の当たり判定の代わりに、矩形と点の当たり判定を追加

    def draw(self):
        pyxel.cls(0)
        # 円を描画する
        #pyxel.circ(self.x1, self.y1, self.SIZE1, 9)
        #pyxel.circ(self.x2, self.y2, self.SIZE2, 11)
        # 矩形を描画する
        pyxel.rect(self.x1, self.y1, self.x1+self.SIZE1, self.y1+self.SIZE1, 9)
        pyxel.rect(self.x2, self.y2, self.x2+self.SIZE2, self.y2+self.SIZE2, 11)

        # 座標を描画する
        pyxel.text(0, 0, "ORANGE: %d,%d"%(self.x1, self.y1), 9)
        pyxel.text(0, 8, "GREEN: %d,%d"%(self.x2, self.y2), 11)

        # 二点間を線でつなぐ
        pyxel.line(self.x1, self.y1, self.x2, self.y2, 7)

        # 二点間の距離を求める
        dx = self.x2 - self.x1
        dy = self.y2 - self.y1
        distance = math.sqrt(dx*dx + dy*dy)
        pyxel.text(0, 16, "DISTANCE:%f"%distance, 7)

        # 円での当たり判定
        #if distance < self.SIZE1 + self.SIZE2:
        #    pyxel.text(0, 24, "HIT!", 7)
        
        # 矩形と点の当たり判定
        left1   = self.x1
        top1    = self.y1
        right1  = self.x1 + self.SIZE1
        bottom1 = self.y1 + self.SIZE1
        if left1 <= self.x2 <= right1:
            if top1 <= self.y2 <= bottom1:
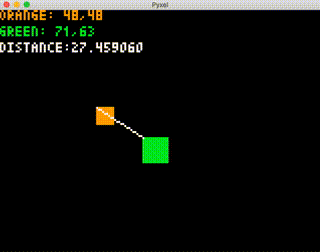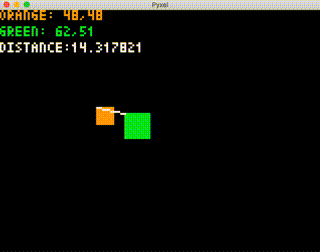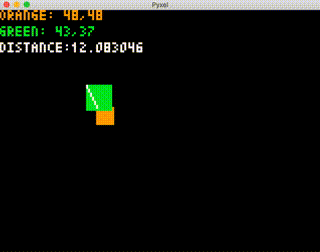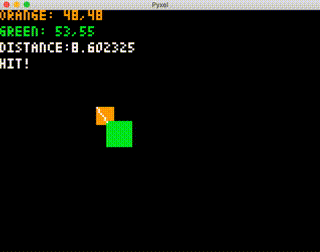
                pyxel.text(0, 24, "HIT!", 7)

実行して、オレンジの矩形に緑の矩形の左上が入ると、"HIT!" の文字が表示されることを確認します。
この段階では、点で判定しているだけなので、緑の右下が入っても "HIT!" は表示されません。

これを踏まえて矩形同士の判定なのですが、実は簡単にはできません。

点を組み合わせて判定するだけだと、見た目では当たっているものの、当たり判定が発生しないケースが発生します。このような状況を「コリジョン抜け」と呼んだりします。

ではどのように判定するのかというと、「絶対に当たらない状況」の逆は当たっている、という逆転の発想をします。

これらはいずれも「絶対に重ならない」条件となります。ですので、いずれかの条件が成立していれば「当たっていない」という判定をすることができます。
では、当たり判定の部分を以下のように修正します。

        # 矩形同士の当たり判定
        left1   = self.x1
        top1    = self.y1
        right1  = self.x1 + self.SIZE1
        bottom1 = self.y1 + self.SIZE1
        left2   = self.x2
        top2    = self.y2
        right2  = self.x2 + self.SIZE2
        bottom2 = self.y2 + self.SIZE2
        if right2 < left1 or right1 < left2 or bottom2 < top1 or bottom1 < top2:
            pass
        else:
            pyxel.text(0, 24, "HIT!", 7)

条件が成立した場合は pass で何もせずに、else文に入った時に「当たり」とします。

では実行して、正しく当たり判定が行われるかどうかを確認します。

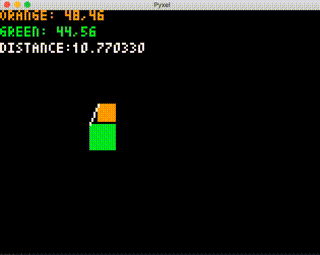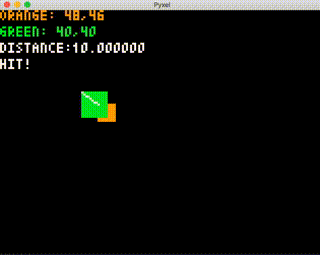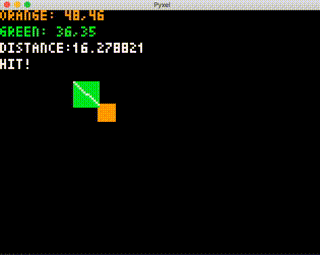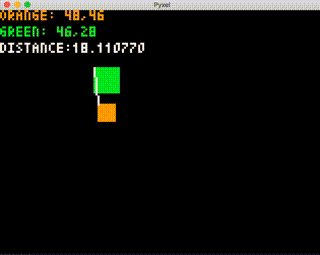
動作チェックとしては、角の4点が入った時に "HIT!" と表示される、角の4点が入っていなくても重なりがあれば "HIT!" と表示される、ということをしっかり動作確認してみてください。

なお、この条件判定は「ド・モルガンの法則」を使うともう少しシンプルにできます。ド・モルガンの法則とは、あるルールにしたがって条件式を入れ替えると、それによって得られる結果を逆にできる、という法則です。
具体的には、以下の入れ替えを行います。

* 不等式を逆にする
* and を or 、or を and にする
* True を False、False を True にする

これを行うと、プログラムは以下のように書き換えることができます。

       if right2 > left1 and right1 > left2 and bottom2 > top1 and bottom1 > top2:
            pyxel.text(0, 24, "HIT!", 7)

正確には "<" の反対は ">=" なのですが、簡易的に書きました。当たりの境界判定をしっかり行う場合には、このあたりに注意する必要があります。

■参考書籍

ゲーム開発のための数学・物理学入門 改訂版 (Professional game programming)

基本的なゲーム数学、物理の情報がまとまっていてオススメです。この記事はこの本を参考にしています。
私がゲームの専門学校に通っているときはこの本で勉強していました。(正確には下の改定前の本ですが)

ゲーム開発のための数学・物理学入門 Beginning Math and Physics for Game Programmers

中古本に抵抗のない人であれば、改定前のこちらの本が安くてオススメです。

ゲームを動かす数学・物理

こちらの本も具体的でわかりやすく、ゲームプログラマーの方が書いているので、実務に近い印象を受けました。オススメの本です。